Reciprocal rule
Encyclopedia
In calculus
, the reciprocal rule is a shorthand method of finding the derivative
of a function
that is the reciprocal
of a differentiable function, without using the quotient rule or chain rule
.
The reciprocal rule states that the derivative of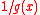
is given by
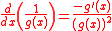
where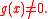
. Then,
, by a process very much like that of the derivation of the quotient rule. One thinks of
as being the function 
composed with the function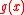 
. The result then follows by application of the chain rule.
is:
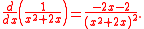
The derivative of
(when 
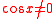) is:
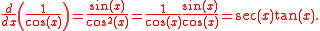
For more general examples, see the derivative
article.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the reciprocal rule is a shorthand method of finding the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of a differentiable function, without using the quotient rule or chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
.
The reciprocal rule states that the derivative of
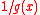is given by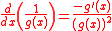where
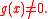
From the quotient rule
The reciprocal rule is derived from the quotient rule, with the numerator. Then,
 |
 |
 |
|
 |
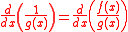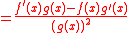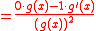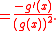From the chain rule
It is also possible to derive the reciprocal rule from the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, by a process very much like that of the derivation of the quotient rule. One thinks of
as being the function composed with the function 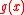. The result then follows by application of the chain rule.Examples
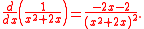
The derivative of is:The derivative of
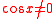(when ) is: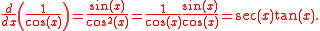For more general examples, see the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
article.