
Nachbin's theorem
Encyclopedia
In mathematics
, in the area of complex analysis
, Nachbin's theorem (named after Leopoldo Nachbin
) is commonly used to establish a bound on the growth rates for an analytic function
. This article will provide a brief review of growth rates, including the idea of a function of exponential type. Classification of growth rates based on type help provide a finer tool than big O
or Landau notation, since a number of theorems about the analytic structure of the bounded function and its integral transforms can be stated. In particular, Nachbin's theorem may be used to give the domain of convergence of the generalized Borel transform, given below.
is said to be of exponential type if there exist constants M and τ such that
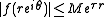
in the limit of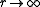 . Here, the complex variable z was written as
. Here, the complex variable z was written as 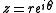 to emphasize that the limit must hold in all directions θ. Letting τ stand for the infimum
to emphasize that the limit must hold in all directions θ. Letting τ stand for the infimum
of all such τ, one then says that the function f is of exponential type τ.
For example, let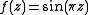 . Then one says that
. Then one says that 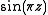 is of exponential type π, since π is the smallest number that bounds the growth of
is of exponential type π, since π is the smallest number that bounds the growth of 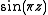 along the imaginary axis. So, for this example, Carlson's theorem
along the imaginary axis. So, for this example, Carlson's theorem
cannot apply, as it requires functions of exponential type less than π.
 is a comparison function if it has a series
is a comparison function if it has a series
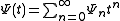
with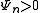 for all n, and
for all n, and
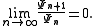
Note that comparison functions are necessarily entire
, which follows from the ratio test. If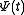 is such a comparison function, one then says that f is of Ψ-type if there exist constants M and τ such that
is such a comparison function, one then says that f is of Ψ-type if there exist constants M and τ such that
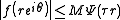
as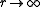 . If τ is the infimum of all such τ one says that f is of Ψ-type τ.
. If τ is the infimum of all such τ one says that f is of Ψ-type τ.
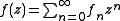
is of Ψ-type τ if and only if
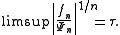
-like situations, and for integral transforms. For example, the generalized Borel transform is given by
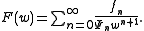
If f is of Ψ-type τ, then the exterior of the domain of convergence of , and all of its singular points, are contained within the disk
, and all of its singular points, are contained within the disk
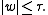
Furthermore, one has
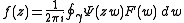
where the contour of integration γ encircles the disk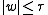 . This generalizes the usual Borel transform for exponential type, where
. This generalizes the usual Borel transform for exponential type, where 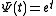 . The integral form for the generalized Borel transform follows as well. Let
. The integral form for the generalized Borel transform follows as well. Let 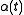 be a function whose first derivative is bounded on the interval
be a function whose first derivative is bounded on the interval 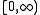 , so that
, so that
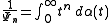
where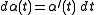 . Then the integral form of the generalized Borel transform is
. Then the integral form of the generalized Borel transform is
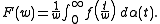
The ordinary Borel transform is regained by setting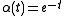 . Note that the integral form of the Borel transform is just the Laplace transform.
. Note that the integral form of the Borel transform is just the Laplace transform.

where f(t) may or may not be of exponential growth and the kernel K(u) has a Mellin transform
. The solution, pointed out by L. Nachbin himself, can be obtained as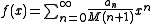 with
with 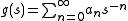 and M(n) is the Mellin transform of K(u).
and M(n) is the Mellin transform of K(u).
 can form a complete
can form a complete
uniform space
, namely a Fréchet space
, by the topology
induced by the countable family of norm
s
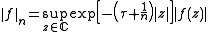
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, Nachbin's theorem (named after Leopoldo Nachbin
Leopoldo Nachbin
Leopoldo Nachbin was a Brazilian mathematician who is best known for Nachbin's theorem.-External links:*...
) is commonly used to establish a bound on the growth rates for an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. This article will provide a brief review of growth rates, including the idea of a function of exponential type. Classification of growth rates based on type help provide a finer tool than big O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
or Landau notation, since a number of theorems about the analytic structure of the bounded function and its integral transforms can be stated. In particular, Nachbin's theorem may be used to give the domain of convergence of the generalized Borel transform, given below.
Exponential type
A function f(z) defined on the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is said to be of exponential type if there exist constants M and τ such that
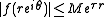
in the limit of
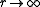 . Here, the complex variable z was written as
. Here, the complex variable z was written as 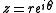 to emphasize that the limit must hold in all directions θ. Letting τ stand for the infimum
to emphasize that the limit must hold in all directions θ. Letting τ stand for the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of all such τ, one then says that the function f is of exponential type τ.
For example, let
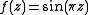 . Then one says that
. Then one says that 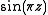 is of exponential type π, since π is the smallest number that bounds the growth of
is of exponential type π, since π is the smallest number that bounds the growth of 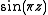 along the imaginary axis. So, for this example, Carlson's theorem
along the imaginary axis. So, for this example, Carlson's theoremCarlson's theorem
In mathematics, in the area of complex analysis, Carlson's theorem is a uniqueness theorem about a summable expansion of an analytic function. It is typically invoked to defend the uniqueness of a Newton series expansion. Carlson's theorem has generalized analogues for expansions in other bases of...
cannot apply, as it requires functions of exponential type less than π.
Ψ type
Bounding may be defined for other functions besides the exponential function. In general, a function is a comparison function if it has a series
is a comparison function if it has a series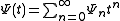
with
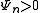 for all n, and
for all n, and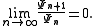
Note that comparison functions are necessarily entire
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
, which follows from the ratio test. If
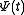 is such a comparison function, one then says that f is of Ψ-type if there exist constants M and τ such that
is such a comparison function, one then says that f is of Ψ-type if there exist constants M and τ such that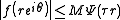
as
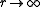 . If τ is the infimum of all such τ one says that f is of Ψ-type τ.
. If τ is the infimum of all such τ one says that f is of Ψ-type τ.Nachbin's theorem
Nachbin's theorem states that a function f(z) with the series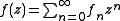
is of Ψ-type τ if and only if
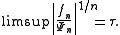
Borel transform
Nachbin's theorem has immediate applications in Cauchy theoremCauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
-like situations, and for integral transforms. For example, the generalized Borel transform is given by
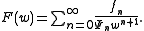
If f is of Ψ-type τ, then the exterior of the domain of convergence of
 , and all of its singular points, are contained within the disk
, and all of its singular points, are contained within the disk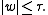
Furthermore, one has
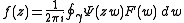
where the contour of integration γ encircles the disk
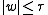 . This generalizes the usual Borel transform for exponential type, where
. This generalizes the usual Borel transform for exponential type, where 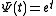 . The integral form for the generalized Borel transform follows as well. Let
. The integral form for the generalized Borel transform follows as well. Let 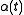 be a function whose first derivative is bounded on the interval
be a function whose first derivative is bounded on the interval 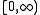 , so that
, so that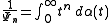
where
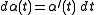 . Then the integral form of the generalized Borel transform is
. Then the integral form of the generalized Borel transform is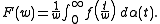
The ordinary Borel transform is regained by setting
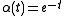 . Note that the integral form of the Borel transform is just the Laplace transform.
. Note that the integral form of the Borel transform is just the Laplace transform.Nachbin resummation
Nachbin resummation (generalized Borel transform) can be used to sum divergent series that escape to the usual Borel resummation or even to solve (asymptotically) integral equations of the form:
where f(t) may or may not be of exponential growth and the kernel K(u) has a Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
. The solution, pointed out by L. Nachbin himself, can be obtained as
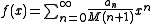 with
with 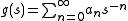 and M(n) is the Mellin transform of K(u).
and M(n) is the Mellin transform of K(u).Fréchet space
Collections of functions of exponential type can form a complete
can form a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
, namely a Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
, by the topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
induced by the countable family of norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
s
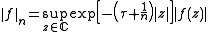
See also
- Divergent seriesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
- Euler summationEuler summationEuler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
- Cesàro summationCesàro summationIn mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
- Lambert summationLambert summationIn mathematical analysis, Lambert summation is a summability method for a class of divergent series.-Definition:A series \sum a_n is Lambert summable to A, written \sum a_n = A , if...
- Nachbin resummation
- Phragmén–Lindelöf principle
- Abelian and tauberian theoremsAbelian and tauberian theoremsIn mathematics, abelian and tauberian theorems are theorems giving conditions for two methods of summing divergent series to give the same result, named after Niels Henrik Abel and Alfred Tauber...
- Van Wijngaarden transformation

