Van Wijngaarden transformation
Encyclopedia
In mathematics
and numerical analysis
, in order to accelerate convergence of an alternating series, Euler's transform can be computed as follows.
Compute a row of partial sums :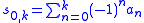
and form rows of averages between neighbors,
The first column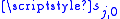
then contains the partial sums of the Euler transform.
Adriaan van Wijngaarden
's contribution was to point out that it is better not to carry this procedure through to the very end, but to stop two-thirds of the way. If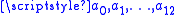
are available, then 
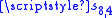is almost always a better approximation to the sum than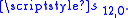 
Leibniz formula for pi,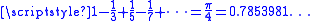
, gives the partial sum 
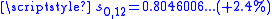, the Euler transform partial sum 
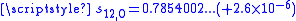and the van Wijngaarden result 
(relative errors are in round brackets).
1.00000000 0.66666667 0.86666667 0.72380952 0.83492063 0.74401154 0.82093462 0.75426795 0.81309148 0.76045990 0.80807895 0.76460069 0.80460069
0.83333333 0.76666667 0.79523810 0.77936508 0.78946609 0.78247308 0.78760129 0.78367972 0.78677569 0.78426943 0.78633982 0.78460069
0.80000000 0.78095238 0.78730159 0.78441558 0.78596959 0.78503719 0.78564050 0.78522771 0.78552256 0.78530463 0.78547026
0.79047619 0.78412698 0.78585859 0.78519259 0.78550339 0.78533884 0.78543410 0.78537513 0.78541359 0.78538744
0.78730159 0.78499278 0.78552559 0.78534799 0.78542111 0.78538647 0.78540462 0.78539436 0.78540052
0.78614719 0.78525919 0.78543679 0.78538455 0.78540379 0.78539555 0.78539949 0.78539744
0.78570319 0.78534799 0.78541067 0.78539417 0.78539967 0.78539752 0.78539847
0.78552559 0.78537933 0.78540242 0.78539692 0.78539860 0.78539799
0.78545246 0.78539087 0.78539967 0.78539776 0.78539829
0.78542166 0.78539527 0.78539871 0.78539803
0.78540847 0.78539699 0.78539837
0.78540273 0.78539768
0.78540021
This table results from the J
formula 'b11.8'8!:2-:&(}:+}.)^:n+/\(_1^n)*%1+2*n=.i.13
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, in order to accelerate convergence of an alternating series, Euler's transform can be computed as follows.
Compute a row of partial sums :
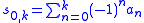
and form rows of averages between neighbors,
The first column
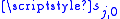then contains the partial sums of the Euler transform.Adriaan van Wijngaarden
Adriaan van Wijngaarden
Adriaan van Wijngaarden was an important mathematician and computer scientist who is considered by many to have been the founding father of informatica in the Netherlands...
's contribution was to point out that it is better not to carry this procedure through to the very end, but to stop two-thirds of the way. If
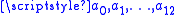are available, then 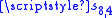is almost always a better approximation to the sum than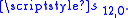 Leibniz formula for pi,
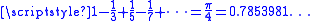, gives the partial sum 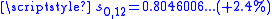, the Euler transform partial sum 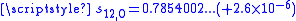and the van Wijngaarden result (relative errors are in round brackets).1.00000000 0.66666667 0.86666667 0.72380952 0.83492063 0.74401154 0.82093462 0.75426795 0.81309148 0.76045990 0.80807895 0.76460069 0.80460069
0.83333333 0.76666667 0.79523810 0.77936508 0.78946609 0.78247308 0.78760129 0.78367972 0.78677569 0.78426943 0.78633982 0.78460069
0.80000000 0.78095238 0.78730159 0.78441558 0.78596959 0.78503719 0.78564050 0.78522771 0.78552256 0.78530463 0.78547026
0.79047619 0.78412698 0.78585859 0.78519259 0.78550339 0.78533884 0.78543410 0.78537513 0.78541359 0.78538744
0.78730159 0.78499278 0.78552559 0.78534799 0.78542111 0.78538647 0.78540462 0.78539436 0.78540052
0.78614719 0.78525919 0.78543679 0.78538455 0.78540379 0.78539555 0.78539949 0.78539744
0.78570319 0.78534799 0.78541067 0.78539417 0.78539967 0.78539752 0.78539847
0.78552559 0.78537933 0.78540242 0.78539692 0.78539860 0.78539799
0.78545246 0.78539087 0.78539967 0.78539776 0.78539829
0.78542166 0.78539527 0.78539871 0.78539803
0.78540847 0.78539699 0.78539837
0.78540273 0.78539768
0.78540021
This table results from the J
J (programming language)
The J programming language, developed in the early 1990s by Kenneth E. Iverson and Roger Hui, is a synthesis of APL and the FP and FL function-level languages created by John Backus....
formula 'b11.8'8!:2-:&(}:+}.)^:n+/\(_1^n)*%1+2*n=.i.13