Motor variable
Encyclopedia
A function of a motor variable is a function
with arguments and values in the split-complex number
plane, much as functions of a complex variable involve ordinary complex number
s. The split-complex numbers lie in the motor plane D, a term referring to algebraic kinematics developed by William Kingdon Clifford
.
For example,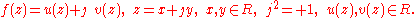
Analogous to planar mapping with ordinary complex number variables, functions depending on a motor variable provide a tool for mathematical model
s.
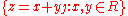, the split-complex plane. The following exemplar functions f have domain and range in D:
The action of a hyperbolic versor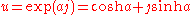
is combined with translation
to produce the affine transformation
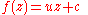.When c = 0, the function is equivalent to a squeeze mapping
.
The squaring function has no analogy in ordinary complex arithmetic. Let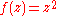
and note that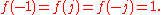 
The result is that the four quadrants are mapped into one, the identity component
:
.
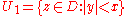Note that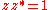
forms the unit hyperbola
. Thus the
reciprocation
involves the hyperbola as curve of reference as opposed to the circle in C.
On the extended complex plane one has the class of functions called Mobius transformations. For the motor variable the analogous functions are constructed with inversive ring geometry
:
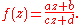
The extension of the split-complex plane to make these mappings bijective is a part of the subject of inversive split-complex geometry.
On the ordinary complex plane, the Cayley transform carries the upper half-plane to the unit disk, thus bounding it. A mapping of the identity component U1 into a rectangle provides a comparable bounding action: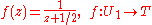
where T = {z = x + j y : |y| < x < 1 or |y| < x − 1 when 1
carries the whole plane D into U1: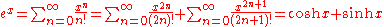
.
Thus when x = bj , then ex is a hyperbolic versor. For the general motor variable z = a + bj , one has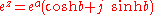
.
In the theory of functions of a motor variable special attention should be called to the square root and logarithm functions. In particular, the plane of split-complex numbers consists of four connected component
s and the set of singular points that have no inverse: the diagonals z = x ± x j, x ∈ R. The identity component
, namely {z : x > |y| }, is the range
of the squaring function and the exponential. Thus it is the domain of the square root and logarithm functions. The other three quadrants do not belong in the domain because square root and logarithm are defined as one-to-one inverses of the squaring function and the exponential function.
The consequent partial differential equation
s are called "Scheffers' conditions" by
Isaak Yaglom
who credits Georg Scheffers
' work of 1893. See Duren's text for the use of
similar differential operators to establish the relation of harmonic function theory to
analytic functions on the ordinary complex plane C .It is apparent that the components u
and v of a D-holomorphic function f satisfy the wave equation
, associated with
D'Alembert, whereas components of C-holomorphic functions satisfy Laplace's equation
.
He then proceeds, for example, to generalize theorems due to Cauchy, Abel, Mertens, and Hardy to the domain of the motor variable.
Vignaux completed his series with a six page note on the approximation of D-holomorphic functions in a unit isotropic rectangle by Bernstein polynomials.While there are some typographical errors as well as a couple of technical stumbles in this series, Vignaux succeeded in laying out the main lines of the theory that lies between real and ordinary complex analysis. The text is especially impressive as an instructive document for students and teachers due to its exemplary development from elements. Furthermore, the entire excursion is rooted in “its relation to Émile Borel
’s geometry” so as to underwrite its motivation.
recalled the tessarine algebra as bicomplex numbers. Naturally the subalgebra of real tessarines arose and came to be called the bireal numbers.
In 1946 U. Bencivenga published an essay on the dual number
s and the split-complex numbers where he used the term bireal number. He also described some of the function theory of the bireal variable. The essay was studied at University of British Columbia
in 1949 when Geoffry Fox wrote his master’s thesis "Elementary function theory of a hypercomplex variable and the theory of conformal mapping in the hyperbolic plane". On page 46 Fox reports "Bencivenga has shown that a function of a bireal variable maps the hyperbolic plane into itself in such a manner that, at those points for which the derivative of a function exists and does not vanish, hyperbolic angles are preserved in the mapping".
G. Fox proceeds to provide the polar decomposition of a bireal variable and discusses hyperbolic orthogonality. Starting from a different definition he proves on page 57
Fox focuses on "bilinear transformations"
are bireal constants. To cope with singularity he augments the plane with a single point at infinity (page 73).
Among his novel contributions to function theory is the concept of an interlocked system. Fox shows that for a bireal k satisfying
the hyperbolas
do not intersect (form an interlocked system). He then shows that this property is preserved by bilinear transformations of a bireal variable.
. With the adoption of motor variables the traditional expectations are countered. The reason is that (D, + , × ) does not form a unique factorization domain
. Substitute structures for the motor plane were provided by Poodiack and LeClair in 2009. They prove three versions of the fundamental theorem of algebra where a polynomial of degree n has n2 roots counting multiplicity. To provide an appropriate concept for multiplicity, they construct a matrix which contains all the roots of a polynomial. Furthermore, their method allows derivation of a similar theorem for polynomials with tessarine
coefficients. The article in The College Mathematics Journal uses the term "perplex number" for a motor variable, and the term "hyperbolic number" for a tessarine. A basic example of the non-unique factorization is
exhibiting the set {1, −1, j, −j } of four roots to the second degree polynomial.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with arguments and values in the split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
plane, much as functions of a complex variable involve ordinary complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. The split-complex numbers lie in the motor plane D, a term referring to algebraic kinematics developed by William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
.
For example,
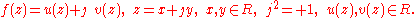
Analogous to planar mapping with ordinary complex number variables, functions depending on a motor variable provide a tool for mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s.
Elementary functions of a motor variable
Let D =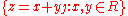, the split-complex plane. The following exemplar functions f have domain and range in D:The action of a hyperbolic versor
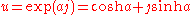is combined with translationTranslation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
to produce the affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
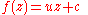.When c = 0, the function is equivalent to a squeeze mappingSqueeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
.
The squaring function has no analogy in ordinary complex arithmetic. Let
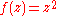and note that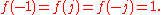 The result is that the four quadrants are mapped into one, the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
:
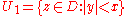.Note that
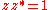forms the unit hyperbolaUnit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
. Thus thereciprocation
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
involves the hyperbola as curve of reference as opposed to the circle in C.
On the extended complex plane one has the class of functions called Mobius transformations. For the motor variable the analogous functions are constructed with inversive ring geometry
Inversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
:
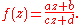
The extension of the split-complex plane to make these mappings bijective is a part of the subject of inversive split-complex geometry.
On the ordinary complex plane, the Cayley transform carries the upper half-plane to the unit disk, thus bounding it. A mapping of the identity component U1 into a rectangle provides a comparable bounding action:
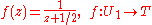
where T = {z = x + j y : |y| < x < 1 or |y| < x − 1 when 1
Exp, log, and square root
The exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
carries the whole plane D into U1:
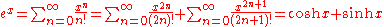.Thus when x = bj , then ex is a hyperbolic versor. For the general motor variable z = a + bj , one has
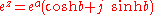.In the theory of functions of a motor variable special attention should be called to the square root and logarithm functions. In particular, the plane of split-complex numbers consists of four connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s and the set of singular points that have no inverse: the diagonals z = x ± x j, x ∈ R. The identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
, namely {z : x > |y| }, is the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of the squaring function and the exponential. Thus it is the domain of the square root and logarithm functions. The other three quadrants do not belong in the domain because square root and logarithm are defined as one-to-one inverses of the squaring function and the exponential function.
D-holomorphic functions
The function f is called D-holomorphic when- 0 = (∂/∂x − j ∂/∂y) ( u + j v)
- = ux − j2 vy + j (vx − uy ).
The consequent partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s are called "Scheffers' conditions" by
Isaak Yaglom
Isaak Yaglom
Isaak Moiseevich Yaglom was a Soviet mathematician and author of popular mathematics books, some with his twin Akiva Yaglom.Yaglom received a Ph.D. from Moscow State University in 1945 as student of Veniamin Kagan. As the author of several books, translated into English, that have become academic...
who credits Georg Scheffers
Georg Scheffers
Georg Scheffers was a German mathematician specializing in differential geometry. He was born on November 21, 1899 in the village of Altendorf near Holzminden . Scheffers began his university career at the University of Leipzig where he studied with Felix Klein and Sophus Lie...
' work of 1893. See Duren's text for the use of
similar differential operators to establish the relation of harmonic function theory to
analytic functions on the ordinary complex plane C .It is apparent that the components u
and v of a D-holomorphic function f satisfy the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, associated with
D'Alembert, whereas components of C-holomorphic functions satisfy Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
.
La Plata lessons
At the National University of La Plata in 1935, J.C. Vignaux, an expert in convergence of infinite series, contributed four articles on the motor variable to the university’s annual periodical. He is the sole author of the introductory one, and consulted with his department head A. Durañona y Vedia on the others. In "Sobre las series de numeros complejos hiperbolicos" he says (p.123):- This system of hyperbolic complex numbers [motor variables] is the direct sum of two fields isomorphic to the field of real numbers; this property permits explication of the theory of series and of functions of the hyperbolic complex variable through the use of properties of the field of real numbers.
He then proceeds, for example, to generalize theorems due to Cauchy, Abel, Mertens, and Hardy to the domain of the motor variable.
In the primary article, cited below, he considers D-holomorphic functions, and the satisfaction of d’Alembert’s equation by their components. He calls a rectangle with sides parallel to the diagonals y = x and y = − x, an isotropic rectangle.He concludes his abstract with these words:
- Isotropic rectangles play a fundamental role in this theory since they form the domains of existence for holomorphic functions, domains of convergence of power series, and domains of convergence of functional series.
Vignaux completed his series with a six page note on the approximation of D-holomorphic functions in a unit isotropic rectangle by Bernstein polynomials.While there are some typographical errors as well as a couple of technical stumbles in this series, Vignaux succeeded in laying out the main lines of the theory that lies between real and ordinary complex analysis. The text is especially impressive as an instructive document for students and teachers due to its exemplary development from elements. Furthermore, the entire excursion is rooted in “its relation to Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
’s geometry” so as to underwrite its motivation.
Bireal variable
In 1892 Corrado SegreCorrado Segre
Corrado Segre was an Italian mathematician who is remembered today as a major contributor to the early development of algebraic geometry....
recalled the tessarine algebra as bicomplex numbers. Naturally the subalgebra of real tessarines arose and came to be called the bireal numbers.
In 1946 U. Bencivenga published an essay on the dual number
Dual number
In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s and the split-complex numbers where he used the term bireal number. He also described some of the function theory of the bireal variable. The essay was studied at University of British Columbia
University of British Columbia
The University of British Columbia is a public research university. UBC’s two main campuses are situated in Vancouver and in Kelowna in the Okanagan Valley...
in 1949 when Geoffry Fox wrote his master’s thesis "Elementary function theory of a hypercomplex variable and the theory of conformal mapping in the hyperbolic plane". On page 46 Fox reports "Bencivenga has shown that a function of a bireal variable maps the hyperbolic plane into itself in such a manner that, at those points for which the derivative of a function exists and does not vanish, hyperbolic angles are preserved in the mapping".
G. Fox proceeds to provide the polar decomposition of a bireal variable and discusses hyperbolic orthogonality. Starting from a different definition he proves on page 57
- Theorem 3.42 : Two vectors are mutually orthogonal if and only if their unit vectors are mutually reflections of one another in one or another of the diagonal lines through 0.
Fox focuses on "bilinear transformations"
are bireal constants. To cope with singularity he augments the plane with a single point at infinity (page 73).
Among his novel contributions to function theory is the concept of an interlocked system. Fox shows that for a bireal k satisfying
- (a - b)2 < |k| < (a + b)2
the hyperbolas
- | z | = a2 and | z – k | = b2
do not intersect (form an interlocked system). He then shows that this property is preserved by bilinear transformations of a bireal variable.
Polynomial factorization
Two staples of introductory algebra include factorization of polynomials and the fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. With the adoption of motor variables the traditional expectations are countered. The reason is that (D, + , × ) does not form a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
. Substitute structures for the motor plane were provided by Poodiack and LeClair in 2009. They prove three versions of the fundamental theorem of algebra where a polynomial of degree n has n2 roots counting multiplicity. To provide an appropriate concept for multiplicity, they construct a matrix which contains all the roots of a polynomial. Furthermore, their method allows derivation of a similar theorem for polynomials with tessarine
Tessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
coefficients. The article in The College Mathematics Journal uses the term "perplex number" for a motor variable, and the term "hyperbolic number" for a tessarine. A basic example of the non-unique factorization is
exhibiting the set {1, −1, j, −j } of four roots to the second degree polynomial.