Algebraic torus
Encyclopedia
In mathematics
, an algebraic torus is a type of commutative affine algebraic group
. These groups were named by analogy with the theory of tori in Lie group
theory (see maximal torus
). The theory of tori is in some sense opposite to that of unipotent groups, because tori have rich arithmetic structure but no deformations.
S, an algebraic torus over S is defined to be a group scheme
over S that is fpqc locally
isomorphic to a finite product of multiplicative groups. In other words, there exists a faithfully flat map X → S such that any point in X has a quasi-compact open neighborhood U whose image is an open affine in S, such that base change to U yields a finite product of copies of GL1,U = Gm/U. One particularly important case is when S is the spectrum of a field K, making a torus over S an algebraic group whose extension to some finite separable extension L is a finite product of copies of Gm/L. In general, the multiplicity of this product (i.e., the dimension of the scheme) is called the rank of the torus, and it is a locally constant function on S.
If a torus is isomorphic to a product of multiplicative groups Gm/S, the torus is said to be split. All tori over separably closed fields are split, and any non-separably closed field admits a non-split torus given by restriction of scalars
over a separable extension. Restriction of scalars over an inseparable field extension will yield a commutative group scheme that is not a torus.
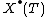is the group of algebraic homomorphisms T → Gm, and the coweight lattice 
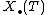is the group of algebraic homomorphisms Gm → T. These are both free abelian groups whose rank is that of the torus, and they have a canonical nondegenerate pairing 
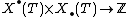given by 
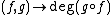, where degree is the number n such that the composition is equal to the nth power map on the multiplicative group. The functor given by taking weights is an antiequivalence of categories between tori and free abelian groups, and the coweight functor is an equivalence. In particular, maps of tori are characterized by linear transformations on weights or coweights, and the automorphism group of a torus is a general linear group over Z. The quasi-inverse of the weights functor is given by a dualization functor from free abelian groups to tori, defined by its functor of points as:
This equivalence can be generalized to pass between groups of multiplicative type (a distinguished class of formal group
s) and arbitrary abelian groups, and such a generalization can be convenient if one wants to work in a well-behaved category, since the category of tori doesn't have kernels or filtered colimits.
When a field K is not separably closed, the weight and coweight lattices of a torus over K are defined as the respective lattices over the separable closure. This induces canonical continuous actions of the absolute Galois group of K on the lattices. The weights and coweights that are fixed by this action are precisely the maps that are defined over K. The functor of taking weights is an antiequivalence between the category of tori over K with algebraic homomorphisms and the category of finitely generated torsion free abelian groups with an action of the absolute Galois group of K.
Given a finite separable field extension L/K and a torus T over K, we have a Galois module
isomorphism
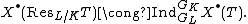
If T is the multiplicative group, then this gives the restriction of scalars a permutation module structure. Tori whose weight lattices are permutation modules for the Galois group are called quasi-split, and all quasi-split tori are finite products of restrictions of scalars.
For a general base scheme S, weights and coweights are defined as fpqc sheaves of free abelian groups on S. These provide representations of fundamental groupoids of the base with respect the fpqc topology. If the torus is locally trivializable with respect to a weaker topology such as the etale topology, then the sheaves of groups descend to the same topologies and these representations factor through the respective quotient groupoids. In particular, an etale sheaf gives rise to a quasi-isotrivial torus, and if S is locally noetherian and normal (more generally, geometrically unibranched
), the torus is isotrivial. As a partial converse, a theorem of Grothendieck asserts that any torus of finite type is quasi-isotrivial, i.e., split by an etale surjection.
Given a rank n torus T over S, a twisted form is a torus over S for which there exists a fpqc covering of S for which their base extensions are isomorphic, i.e., it is a torus of the same rank. Isomorphism classes of twisted forms of a split torus are parametrized by nonabelian flat cohomology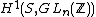
, where the coefficient group forms a constant sheaf. In particular, twisted forms of a split torus T over a field K are parametrized by elements of the Galois cohomology pointed set 
with trivial Galois action on the coefficients. In the one-dimensional case, the coefficients form a group of order two, and isomorphism classes of twisted forms of Gm are in natural bijection with separable quadratic extensions of K.
Since taking a weight lattice is an equivalence of categories, short exact sequences of tori correspond to short exact sequences of the corresponding weight lattices. In particular, extensions of tori are classified by Ext1 sheaves. These are naturally isomorphic to the flat cohomology groups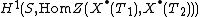
. Over a field, the extensions are parametrized by elements of the corresponding Galois cohomology group.
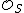-module, and it is a locally constant function on the base. One can also define the degree to be order of the cokernel of the corresponding linear transformation on weight lattices. Two tori are called isogenous if there exists an isogeny between them. An isogeny is an isomorphism if and only if its degree is one. Note that if S doesn't have a map to Spec Q, then the kernel may not be smooth over S.
Given an isogeny f of degree n, one can prove using linear algebra on weights and faithfully flat descent that there exists a dual isogeny g such that gf is the nth power map on the source torus. Therefore, isogeny is an equivalence relation on the category of tori. T. Ono pointed out that two tori over a field are isogenous if and only if their weight lattices are rationally equivalent as Galois modules, where rational equivalence means we tensor over Z with Q and get equivalent vector spaces with Galois action. This extends naturally from Galois modules to fpqc sheaves, where Z and Q are constant sheaves rather than plain groups.
, T. Ono introduced a type of functorial invariants of tori over finite separable extensions of a chosen field k. Such an invariant is a collection of positive real-valued functions fK on isomorphism classes of tori over K, as K runs over finite separable extensions of k, satisfying three properties:
T. Ono showed that the Tamagawa number of a torus over a number field is such an invariant. Furthermore, he showed that it is a quotient of two cohomological invariants, namely the order of the group
(sometimes mistakenly called the Picard group of T, although it doesn't classify Gm torsors over T), and the order of the Tate–Shafarevich group.
The notion of invariant given above generalizes naturally to tori over arbitrary base schemes, with functions taking values in more general rings. While the order of the extension group is a general invariant, the other two invariants above do not seem to have interesting analogues outside the realm of fraction fields of one-dimensional domains and their completions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic torus is a type of commutative affine algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
. These groups were named by analogy with the theory of tori in Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory (see maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
). The theory of tori is in some sense opposite to that of unipotent groups, because tori have rich arithmetic structure but no deformations.
Definition
Given a base schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
S, an algebraic torus over S is defined to be a group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
over S that is fpqc locally
Flat topology
In mathematics, the flat topology is a Grothendieck topology used in algebraic geometry. It is used to define the theory of flat cohomology; it also has played a fundamental role in the theory of descent...
isomorphic to a finite product of multiplicative groups. In other words, there exists a faithfully flat map X → S such that any point in X has a quasi-compact open neighborhood U whose image is an open affine in S, such that base change to U yields a finite product of copies of GL1,U = Gm/U. One particularly important case is when S is the spectrum of a field K, making a torus over S an algebraic group whose extension to some finite separable extension L is a finite product of copies of Gm/L. In general, the multiplicity of this product (i.e., the dimension of the scheme) is called the rank of the torus, and it is a locally constant function on S.
If a torus is isomorphic to a product of multiplicative groups Gm/S, the torus is said to be split. All tori over separably closed fields are split, and any non-separably closed field admits a non-split torus given by restriction of scalars
Weil restriction
In mathematics, restriction of scalars is a functor which, for any finite extension of fields L/k and any algebraic variety X over L, produces another variety ResL/kX, defined over k...
over a separable extension. Restriction of scalars over an inseparable field extension will yield a commutative group scheme that is not a torus.
Weights
Over a separably closed field, a torus T admits two primary invariants. The weight lattice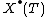 is the group of algebraic homomorphisms T → Gm, and the coweight lattice 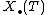is the group of algebraic homomorphisms Gm → T. These are both free abelian groups whose rank is that of the torus, and they have a canonical nondegenerate pairing 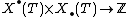given by 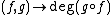, where degree is the number n such that the composition is equal to the nth power map on the multiplicative group. The functor given by taking weights is an antiequivalence of categories between tori and free abelian groups, and the coweight functor is an equivalence. In particular, maps of tori are characterized by linear transformations on weights or coweights, and the automorphism group of a torus is a general linear group over Z. The quasi-inverse of the weights functor is given by a dualization functor from free abelian groups to tori, defined by its functor of points as:This equivalence can be generalized to pass between groups of multiplicative type (a distinguished class of formal group
Formal group
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
s) and arbitrary abelian groups, and such a generalization can be convenient if one wants to work in a well-behaved category, since the category of tori doesn't have kernels or filtered colimits.
When a field K is not separably closed, the weight and coweight lattices of a torus over K are defined as the respective lattices over the separable closure. This induces canonical continuous actions of the absolute Galois group of K on the lattices. The weights and coweights that are fixed by this action are precisely the maps that are defined over K. The functor of taking weights is an antiequivalence between the category of tori over K with algebraic homomorphisms and the category of finitely generated torsion free abelian groups with an action of the absolute Galois group of K.
Given a finite separable field extension L/K and a torus T over K, we have a Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
isomorphism
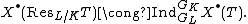
If T is the multiplicative group, then this gives the restriction of scalars a permutation module structure. Tori whose weight lattices are permutation modules for the Galois group are called quasi-split, and all quasi-split tori are finite products of restrictions of scalars.
For a general base scheme S, weights and coweights are defined as fpqc sheaves of free abelian groups on S. These provide representations of fundamental groupoids of the base with respect the fpqc topology. If the torus is locally trivializable with respect to a weaker topology such as the etale topology, then the sheaves of groups descend to the same topologies and these representations factor through the respective quotient groupoids. In particular, an etale sheaf gives rise to a quasi-isotrivial torus, and if S is locally noetherian and normal (more generally, geometrically unibranched
Unibranch local ring
In mathematics, specifically in algebraic geometry, a local ring A is said to be unibranch if the reduced ring Ared is an integral domain, and the integral closure B of Ared is also a local ring...
), the torus is isotrivial. As a partial converse, a theorem of Grothendieck asserts that any torus of finite type is quasi-isotrivial, i.e., split by an etale surjection.
Given a rank n torus T over S, a twisted form is a torus over S for which there exists a fpqc covering of S for which their base extensions are isomorphic, i.e., it is a torus of the same rank. Isomorphism classes of twisted forms of a split torus are parametrized by nonabelian flat cohomology
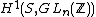, where the coefficient group forms a constant sheaf. In particular, twisted forms of a split torus T over a field K are parametrized by elements of the Galois cohomology pointed set with trivial Galois action on the coefficients. In the one-dimensional case, the coefficients form a group of order two, and isomorphism classes of twisted forms of Gm are in natural bijection with separable quadratic extensions of K.Since taking a weight lattice is an equivalence of categories, short exact sequences of tori correspond to short exact sequences of the corresponding weight lattices. In particular, extensions of tori are classified by Ext1 sheaves. These are naturally isomorphic to the flat cohomology groups
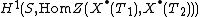. Over a field, the extensions are parametrized by elements of the corresponding Galois cohomology group.Example
Let S be the restriction of scalars of Gm over the field extension C/R. This is a real torus whose real points form the Lie group of nonzero complex numbers. Restriction of scalars gives a canonical embedding of S into GL2, and composition with determinant gives an algebraic homomorphism of tori from S to Gm, called the norm. The kernel of this map is a nonsplit rank one torus called the norm torus of the extension C/R, and its real points form the Lie group U(1), which is topologically a circle. It has no multiplicative subgroups (equivalently, the weight lattice has no nonzero Galois fixed points), and such tori are called anisotropic. Its weight lattice is a copy of the integers, with the nontrivial Galois action that sends complex conjugation to the minus one map.Isogenies
An isogeny is a surjective morphism of tori whose kernel is a finite flat group scheme. Equivalently, it is an injection of the corresponding weight lattices with finite cokernel. The degree of the isogeny is defined to be the order of the kernel, i.e., the rank of its structure sheaf as a locally free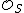-module, and it is a locally constant function on the base. One can also define the degree to be order of the cokernel of the corresponding linear transformation on weight lattices. Two tori are called isogenous if there exists an isogeny between them. An isogeny is an isomorphism if and only if its degree is one. Note that if S doesn't have a map to Spec Q, then the kernel may not be smooth over S.Given an isogeny f of degree n, one can prove using linear algebra on weights and faithfully flat descent that there exists a dual isogeny g such that gf is the nth power map on the source torus. Therefore, isogeny is an equivalence relation on the category of tori. T. Ono pointed out that two tori over a field are isogenous if and only if their weight lattices are rationally equivalent as Galois modules, where rational equivalence means we tensor over Z with Q and get equivalent vector spaces with Galois action. This extends naturally from Galois modules to fpqc sheaves, where Z and Q are constant sheaves rather than plain groups.
Arithmetic invariants
In his work on Tamagawa numbersWeil conjecture on Tamagawa numbers
In mathematics, the Weil conjecture on Tamagawa numbers is a result about algebraic groups formulated by André Weil in the late 1950s and proved in 1989...
, T. Ono introduced a type of functorial invariants of tori over finite separable extensions of a chosen field k. Such an invariant is a collection of positive real-valued functions fK on isomorphism classes of tori over K, as K runs over finite separable extensions of k, satisfying three properties:
- Multiplicativity: Given two tori T1 and T2 over K, fK(T1 × T2) = fK(T1) fK(T2)
- Restriction: For a finite separable extension L/K, fL evaluated on an L torus is equal to fK evaluated on its restriction of scalars to K.
- Projective triviality: If T is a torus over K whose weight lattice is a projective Galois module, then fK(T) = 1.
T. Ono showed that the Tamagawa number of a torus over a number field is such an invariant. Furthermore, he showed that it is a quotient of two cohomological invariants, namely the order of the group
(sometimes mistakenly called the Picard group of T, although it doesn't classify Gm torsors over T), and the order of the Tate–Shafarevich group.The notion of invariant given above generalizes naturally to tori over arbitrary base schemes, with functions taking values in more general rings. While the order of the extension group is a general invariant, the other two invariants above do not seem to have interesting analogues outside the realm of fraction fields of one-dimensional domains and their completions.