Two-sided Laplace transform
Encyclopedia
In mathematics
, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform
, the Mellin transform
, and the ordinary or one-sided Laplace transform. If ƒ(t) is a real or complex valued function of the real variable t defined for all real numbers, then the two-sided Laplace transform is defined by the integral
The integral is most commonly understood as an improper integral
, which converges if and only if each of the integrals
exists. There seems to be no generally accepted notation for the two-sided transform; the
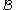used here recalls "bilateral". The two-sided transform
used by some authors is
In pure mathematics the argument t can be any variable, and Laplace transforms are used to study how Differential operator
s transform the function.
In science
and engineering
applications, the argument t often represents time (in seconds), and the function ƒ(t) often represents a signal or waveform that varies with time. In these cases, the signals are transformed by filters
, that work like a mathematical operator, but with a restriction. They have to be causal, which means that the output in a given time t cannot depend of input values in higher values of t.
When working with functions of time, ƒ(t) is called the time domain representation of the signal, while F(s) is called the s-domain representation. The inverse transformation then represents a synthesis of the signal as the sum of its frequency components taken over all frequencies, whereas the forward transformation represents the analysis of the signal into its frequency components.
, equal to zero when t is less than zero, to one-half when t equals zero, and to one when t is greater than zero, then the Laplace transform
may be defined in terms of the two-sided Laplace transform by
On the other hand, we also have
so either version of the Laplace transform can be defined in terms of the other.
The Mellin transform
may be defined in terms of the two-sided Laplace
transform by
and conversely we can get the two-sided transform from the Mellin transform by
The Fourier transform may also be defined in terms of the two-sided Laplace
transform; here instead of having the same image with differing originals, we
have the same original but different images. We may define the Fourier transform
as
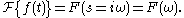
Note that definitions of the Fourier transform differ, and in particular
is often used instead. In terms of the Fourier transform, we may also obtain the two-sided Laplace transform, as
The Fourier transform is normally defined so that it exists for real values; the above definition defines the image in a strip
which may not include the real axis.
The moment-generating function
of a continuous probability density function
ƒ(x) can be expressed as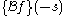
.
|+ Properties of the unilateral Laplace transform
!
! Time domain
! unilateral-'s' domain
! bilateral-'s' domain
|-
! Differentiation
|
|
|
|-
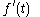
! Second Differentiation
|
|
|
>
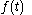
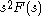To use the bilateral transform is equivalent to assume null initial conditions. Therefore it is more suitable than the unilateral for calculating transfer functions from the differential equations, or when looking for an easy particular solution.
. They make sense when applied over generic functions but when working with functions of time (signals) unilateral transforms are preferred.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
, and the ordinary or one-sided Laplace transform. If ƒ(t) is a real or complex valued function of the real variable t defined for all real numbers, then the two-sided Laplace transform is defined by the integral
The integral is most commonly understood as an improper integral
Improper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
, which converges if and only if each of the integrals
exists. There seems to be no generally accepted notation for the two-sided transform; the
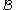used here recalls "bilateral". The two-sided transformused by some authors is
In pure mathematics the argument t can be any variable, and Laplace transforms are used to study how Differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s transform the function.
In science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
applications, the argument t often represents time (in seconds), and the function ƒ(t) often represents a signal or waveform that varies with time. In these cases, the signals are transformed by filters
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
, that work like a mathematical operator, but with a restriction. They have to be causal, which means that the output in a given time t cannot depend of input values in higher values of t.
When working with functions of time, ƒ(t) is called the time domain representation of the signal, while F(s) is called the s-domain representation. The inverse transformation then represents a synthesis of the signal as the sum of its frequency components taken over all frequencies, whereas the forward transformation represents the analysis of the signal into its frequency components.
Relationship to other integral transforms
If u(t) is the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
, equal to zero when t is less than zero, to one-half when t equals zero, and to one when t is greater than zero, then the Laplace transform
may be defined in terms of the two-sided Laplace transform byOn the other hand, we also have
so either version of the Laplace transform can be defined in terms of the other.
The Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
may be defined in terms of the two-sided Laplace
transform by
and conversely we can get the two-sided transform from the Mellin transform by
The Fourier transform may also be defined in terms of the two-sided Laplace
transform; here instead of having the same image with differing originals, we
have the same original but different images. We may define the Fourier transform
as
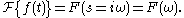
Note that definitions of the Fourier transform differ, and in particular
is often used instead. In terms of the Fourier transform, we may also obtain the two-sided Laplace transform, as
The Fourier transform is normally defined so that it exists for real values; the above definition defines the image in a strip
which may not include the real axis.The moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
of a continuous probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
ƒ(x) can be expressed as
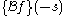.Properties
It has basically the same properties of the unilateral transform with an important difference!
! Time domain
! unilateral-'s' domain
! bilateral-'s' domain
|-
! Differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
|
|
|
|-
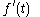
! Second Differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
|
|
|
>
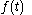
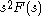To use the bilateral transform is equivalent to assume null initial conditions. Therefore it is more suitable than the unilateral for calculating transfer functions from the differential equations, or when looking for an easy particular solution.
Causality
Bilateral transforms don't respect causalityCausality
Causality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
. They make sense when applied over generic functions but when working with functions of time (signals) unilateral transforms are preferred.
See also
- Causal filterCausal filterIn signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
- Acausal system
- Causal systemCausal systemA causal system is a system where the output depends on past/current inputs but not future inputs i.e...
- Sinc filterSinc filterIn signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
- ideal sinc filter (aka rectangular filter) is acausal and has an infinite delay.