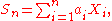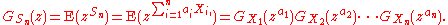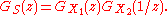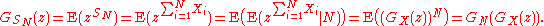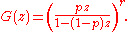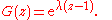Probability-generating function
Encyclopedia
In probability theory
, the probability-generating function of a discrete random variable is a power series representation (the generating function
) of the probability mass function
of the random variable. Probability-generating functions are often employed for their succinct description of the sequence of probabilities Pr(X = i) in the probability mass function for a random variable
X, and to make available the well-developed theory of power series with non-negative coefficients.
s {0,1, ...}, then the probability-generating function of X is defined as
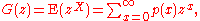
where p is the probability mass function of X. Note that the subscripted notations GX and pX are often used to emphasize that these pertain to a particular random variable X, and to its distribution. The power series converges absolutely
at least for all complex number
s z with |z| ≤ 1; in many examples the radius of convergence is larger.
{0,1, ...}d, then the probability-generating function of X is defined as
where p is the probability mass function of X. The power series converges absolutely at least for all complex vectors with .
, since the probabilities must sum to one. So the radius of convergence
of any probability-generating function must be at least 1, by Abel's theorem
for power series with non-negative coefficients.
1. The probability mass function of X is recovered by taking derivative
s of G
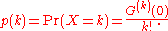
2. It follows from Property 1 that if random variables X and Y have probability generating functions that are equal, GX = GY, then pX = pY. That is, if X and Y have identical probability-generating functions, then they have identical distributions.
3. The normalization of the probability density function can be expressed in terms of the generating function by
The expectation
of X is given by
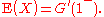
More generally, the kth factorial moment, E(X(X − 1) ... (X − k + 1)), of X is given by
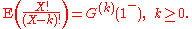
So the variance
of X is given by
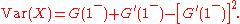
4.GX(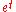
) = MX(t) where X is a random variable, G(t) is the probability generating function and M(t) is the moment-generating function
.
random variables. For example:
of a sequence: see also formal power series
. It is occasionally called the z-transform
of the probability mass function.
Other generating functions of random variables include the moment-generating function
, the characteristic function
and the cumulant generating function.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the probability-generating function of a discrete random variable is a power series representation (the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
) of the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of the random variable. Probability-generating functions are often employed for their succinct description of the sequence of probabilities Pr(X = i) in the probability mass function for a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X, and to make available the well-developed theory of power series with non-negative coefficients.
Univariate case
If X is a discrete random variable taking values in the non-negative integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s {0,1, ...}, then the probability-generating function of X is defined as
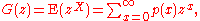
where p is the probability mass function of X. Note that the subscripted notations GX and pX are often used to emphasize that these pertain to a particular random variable X, and to its distribution. The power series converges absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
at least for all complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s z with |z| ≤ 1; in many examples the radius of convergence is larger.
Multivariate case
If is a discrete random variable taking values in the d-dimensional non-negative integer latticeInteger lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
{0,1, ...}d, then the probability-generating function of X is defined as
where p is the probability mass function of X. The power series converges absolutely at least for all complex vectors with .
Power series
Probability-generating functions obey all the rules of power series with non-negative coefficients. In particular, G(1−) = 1, where G(1−) = limz→1G(z) from belowOne-sided limit
In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
, since the probabilities must sum to one. So the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of any probability-generating function must be at least 1, by Abel's theorem
Abel's theorem
In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel.-Theorem:...
for power series with non-negative coefficients.
Probabilities and expectations
The following properties allow the derivation of various basic quantities related to X:1. The probability mass function of X is recovered by taking derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of G
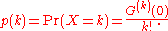
2. It follows from Property 1 that if random variables X and Y have probability generating functions that are equal, GX = GY, then pX = pY. That is, if X and Y have identical probability-generating functions, then they have identical distributions.
3. The normalization of the probability density function can be expressed in terms of the generating function by
The expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of X is given by
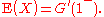
More generally, the kth factorial moment, E(X(X − 1) ... (X − k + 1)), of X is given by
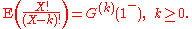
So the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of X is given by
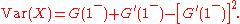
4.GX(
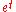) = MX(t) where X is a random variable, G(t) is the probability generating function and M(t) is the moment-generating functionMoment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
.
Functions of independent random variables
Probability-generating functions are particularly useful for dealing with functions of independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables. For example:
- If X1, X2, ..., Xn is a sequence of independent (and not necessarily identically distributed) random variables, and
- where the ai are constants, then the probability-generating function is given by
- For example, if
- then the probability-generating function, GSn(z), is given by
- It also follows that the probability-generating function of the difference of two independent random variables S = X1 − X2 is
- Suppose that N is also an independent, discrete random variable taking values on the non-negative integers, with probability-generating function GN. If the X1, X2, ..., XN are independent and identically distributed with common probability-generating function GX, then
- This can be seen, using the law of total expectationLaw of total expectationThe proposition in probability theory known as the law of total expectation, the law of iterated expectations, the tower rule, the smoothing theorem, among other names, states that if X is an integrable random variable The proposition in probability theory known as the law of total expectation, ...
, as follows:
- This last fact is useful in the study of Galton–Watson processes.
- Suppose again that N is also an independent, discrete random variable taking values on the non-negative integers, with probability-generating function GN and probability density
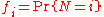. If the X1, X2, ..., XN are independent, but not identically distributed random variables, where 
denotes the probability generating function of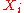 
, then
- For identically distributed Xi this simplifies to the identity stated before. The general case is sometimes useful to obtain a decomposition of SN by means of generating functions.
Examples
- The probability-generating function of a constant random variable, i.e. one with Pr(X = c) = 1, is
- The probability-generating function of a binomial random variable, the number of successes in n trials, with probability p of success in each trial, is
- Note that this is the n-fold product of the probability-generating function of a Bernoulli random variable with parameter p.
- The probability-generating function of a negative binomial random variableNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
, the number of failures occurring before the rth success with probability of success in each trial p, is
- Note that this is the r-fold product of the probability generating function of a geometric random variable.
- The probability-generating function of a Poisson random variablePoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with rate parameter λ is
Related concepts
The probability-generating function is an example of a generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of a sequence: see also formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
. It is occasionally called the z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
of the probability mass function.
Other generating functions of random variables include the moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
, the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
and the cumulant generating function.