In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Young–Fibonacci graph and Young–Fibonacci lattice, named after Alfred Young

Alfred Young

Alfred Young, FRS was a British mathematician.He was born in Widnes, Lancashire, England and educated at Monkton Combe School in Somerset and Clare College, Cambridge, graduating BA as 10th Wrangler in 1895. He is known for his work in the area of group theory...

 and Leonardo Fibonacci, are two closely related structures involving sequences of the digits 1 and 2. Any digit sequence of this type can be assigned a rank, the sum of its digits: for instance, the rank of 11212 is 1 + 1 + 2 + 1 + 2 = 7. As was already known in ancient India, the number of sequences with a given rank is a Fibonacci number

Fibonacci number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....

. The Young–Fibonacci lattice is an infinite modular lattice

Modular lattice

In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨  =  ∧ b,where  ≤  is the partial order, and  ∨  and  ∧  are...

 having these digit sequences as its elements, compatible with this rank structure. The Young–Fibonacci graph is the graph of this lattice, and has a vertex for each digit sequence.

The Young–Fibonacci graph and the Young–Fibonacci lattice were both initially studied in two papers by and . They are named after the closely related Young's lattice

Young's lattice

In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...

 and after the Fibonacci number of their elements at any given rank.

Digit sequences with a given rank

A digit sequence with rank may be formed either by adding the digit 2 to a sequence with rank , or by adding the digit 1 to a sequence with rank . If is the function that maps to the number of different digit sequences of that rank, therefore, satisfies the recurrence relation

Recurrence relation

In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

  defining the Fibonacci

Fibonacci

Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...

 numbers, but with slightly different initial conditions: (there is one rank-0 string, the empty string

Empty string

In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....

, and one rank-1 string, consisting of the single digit 1). These initial conditions cause the sequence of values of to be shifted by one position from the Fibonacci numbers: where denotes the th Fibonacci number.

In the ancient Indian study of prosody, the Fibonacci numbers were used to count the number of different sequences of short and long syllables with a given total length; if the digit 1 corresponds to a short syllable, and the digit 2 corresponds to a long syllable, the rank of a digit sequence measures the total length of the corresponding sequence of syllables. See the Fibonacci number

Fibonacci number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....

 article for details.

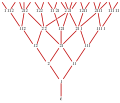
Graphs of digit sequences

The Young–Fibonacci graph is an infinite graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

, with a vertex for each string of the digits “1” and “2” (including the empty string

Empty string

In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....

). The neighbors of a string s are the strings formed from s by one the following operations:

1. Insert a “1” into s, prior to the leftmost “1” (or anywhere in s if it does not already contain a “1”).
2. Change the leftmost “1” of s into a “2”.
3. Remove the leftmost “1” from s.
4. Change a “2” that does not have a “1” to the left of it into a “1”.

It is straightforward to verify that each operation can be inverted: operations 1 and 3 are inverse to each other, as are operations 2 and 4. Therefore, the resulting graph may be considered to be undirected. However, it is usually considered to be a directed acyclic graph

Directed acyclic graph

In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...

 in which each edge connects from a vertex of lower rank to a vertex of higher rank.

As both and observe, this graph has the following properties:

• It is connected: any nonempty string may have its rank reduced by some operation, so there is a sequence of operations leading from it to the empty string, reversing which gives a directed path in the graph from the empty string to every other vertex.
• It is compatible with the rank structure: every directed path has length equal to the difference in ranks of its endpoints.
• For every two nodes u and v, the number of common immediate predecessors of u and v equals the number of common immediate successors of u and v; this number is either zero or one.
• The out-degree of every vertex equals one plus its in-degree.

calls a graph with these properties a Y-graph; calls a graph with a weaker version of these properties (in which the numbers of common predecessors and common successors of any pair of nodes must be equal but may be greater than one) the graph of a differential poset.

Partial order and lattice structure

The transitive closure

Transitive closure

In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...

 of the Young–Fibonacci graph is a partial order. As shows, any two vertices x and y have a unique greatest common predecessor in this order (their meet) and a unique least common successor (their join); thus, this order is a lattice

Lattice (order)

In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...

, called the Young–Fibonacci lattice.

To find the meet of and , one may first test whether one of and is a predecessor of the other. A string is a predecessor of another string in this order exactly when the number of "2" digits remaining in , after removing the longest common suffix of and , is at least as large as the number of all digits remaining in after removing the common suffix. If is a predecessor of according to this test, then their meet is , and similarly if is a predecessor of then their meet is . In a second case, if neither nor is the predecessor of the other, but one or both of them begins with a “1” digit, the meet is unchanged if these initial digits are removed. And finally, if both and begin with the digit “2”, the meet of and may be found by removing this digit from both of them, finding the meet of the resulting suffixes, and adding the “2” back to the start.

A common successor of and (though not necessarily the least common successor) may be found by taking a string of “2” digits with length equal to the longer of and . The least common successor is then the meet of the finitely many strings that are common successors of and and predecessors of this string of “2”s.

As further observes, the Young–Fibonacci lattice is modular

Modular lattice

In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨  =  ∧ b,where  ≤  is the partial order, and  ∨  and  ∧  are...

. incorrectly claims that it is distributive

Distributive lattice

In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...

; however, the sublattice formed by the strings {21,22,121,211,221} forms a diamond sublattice, forbidden in distributive lattices.