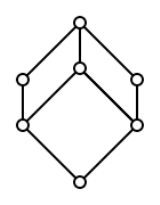
Semimodular lattice
Encyclopedia
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a semimodular lattice, is a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
that satisfies the following condition:
Semimodular law: a ∧ b <: a implies b <: a ∨ b.
The notation a <: b means that b covers a, i.e. a < b and there is no element c such that a < c < b.
An atomistic (hence algebraic
Compact element
In the mathematical area of order theory, the compact or finite elements of a partially ordered set are those elements that cannot be subsumed by a supremum of any non-empty directed set that does not already contain members above the compact element....
) semimodular bounded lattice is called a matroid lattice because such lattices are equivalent to (simple) matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s. An atomistic semimodular bounded lattice of finite length is called a geometric lattice and corresponds to a matroid of finite rank.
Semimodular lattices are also known as upper semimodular lattices; the dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
notion is that of a lower semimodular lattice. A finite lattice is modular
Modular lattice
In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
if and only if it is both upper and lower semimodular.
A finite lattice, or more generally a lattice satisfying the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
or the descending chain condition, is semimodular if and only if it is M-symmetric. Some authors refer to M-symmetric lattices as semimodular lattices.
Birkhoff's condition
A lattice is sometimes called weakly semimodular if it satisfies the following condition due to Garrett BirkhoffGarrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
:
Birkhoff's condition: If a ∧ b <: a and a ∧ b <: b,
- then a <: a ∨ b and b <: a ∨ b.
Every semimodular lattice is weakly semimodular. The converse is true for lattices of finite length, and more generally for upper continuous relatively atomic lattices.
Mac Lane's condition
The following two conditions are equivalent to each other for all lattices. They were found by Saunders Mac LaneSaunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
, who was looking for a condition that is equivalent to semimodularity for finite lattices, but does not involve the covering relation.
Mac Lane's condition 1: For any a, b, c such that b ∧ c < a < c < b ∨ a,
- there is an element d such that b ∧ c < d ≤ b and a = (a ∨ d) ∧ c.
Mac Lane's condition 2: For any a, b, c such that b ∧ c < a < c < b ∨ c,
- there is an element d such that b ∧ c < d ≤ b and a = (a ∨ d) ∧ c.
Every lattice satisfying Mac Lane's condition is semimodular. The converse is true for lattices of finite length, and more generally for relatively atomic lattices. Moreover, every upper continuous lattice satisfying Mac Lane's condition is M-symmetric.

