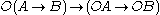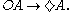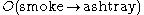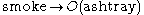Deontic logic
Encyclopedia
Deontic logic is the field of logic
that is concerned with obligation
, permission
, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. Typically, a deontic logic uses OA to mean it is obligatory that A, (or it ought to be (the case) that A), and PA to mean it is permitted (or permissible) that A. The term deontic is derived from the ancient Greek
déon - δέον (gen.: δέοντος), meaning, roughly, that which is binding or proper.
n Mimamsa school
to those of Ancient Greece
have remarked on the formal logical relations of deontic concepts and philosophers from the late Middle Ages
compared deontic concepts with alethic ones. In his Elementa juris naturalis, Leibniz notes the logical relations between the licitum, illicitum, debitum, and indifferens are equivalent to those between the possible, impossible, necessarium, and contingens respectively.
, a pupil of Alexius Meinong
, was the first to propose a formal system of deontic logic in his Grundgesetze des Sollens and he founded it on the syntax of Whitehead's and Russell's propositional calculus
. Mally's deontic vocabulary consisted of the logical constants U and ∩, unary connective !, and binary connectives f and ∞.
Mally defined f, ∞, and ∩ as follows:
Mally proposed five informal principles:
He formalized these principles and took them as his axioms:
From these axioms Mally deduced 35 theorems, many of which he rightly considered strange. Karl Menger
showed that !A ↔ A is a theorem and thus that the introduction of the ! sign is irrelevant and that A ought to be the case if A is the case. After Menger, philosophers no longer considered Mally's system viable. Gert Lokhorst lists Mally's 35 theorems and gives a proof for Menger's theorem at the Stanford Encyclopedia of Philosophy under Mally's Deontic Logic.
The first plausible system of deontic logic was proposed by G. H. von Wright
in his paper Deontic Logic in the philosophical journal Mind in 1951. (Von Wright was also the first to use the term "deontic" in English to refer to this kind of logic although Mally published the German paper Deontik in 1926.) Since the publication of von Wright's seminal paper, many philosophers and computer scientists have investigated and developed systems of deontic logic. Nevertheless, to this day deontic logic remains one of the most controversial and least agreed-upon areas of logic.
G. H. von Wright did not base his 1951 deontic logic on the syntax of the propositional calculus as Mally had done, but was instead influenced by alethic modal logic
s, which Mally had not benefited from. In 1964, von Wright published A New System of Deontic Logic, which was a return to the syntax of the propositional calculus and thus a significant return to Mally's system. (For more on von Wright's departure from and return to the syntax of the propositional calculus, see Deontic Logic: A Personal View and A New System of Deontic Logic, both by Georg Henrik von Wright.) G. H. von Wright's adoption of the modal logic of possibility and necessity for the purposes of normative reasoning was a return to Leibniz.
, and von Wright himself joined this movement. The deontic logic so specified came to be known as "standard deontic logic," often referred to as SDL, KD, or simply D. It can be axiomatized by adding the following axioms to a standard axiomatization of classical propositional logic:
In English, these axioms say, respectively:
FA, meaning it is forbidden that A, can be defined (equivalently) as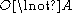
or 
.
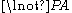There are two main extensions of SDL that are usually considered. The first results by adding an alethic modal operator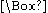
in order to express the Kantian claim that "ought implies can":
where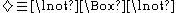
. It is generally assumed that 
is at least a KT operator, but most commonly it is taken to be an S5 operator.
The other main extension results by adding a "conditional obligation" operator O(A/B) read "It is obligatory that A given (or conditional on) B". Motivation for a conditional operator is given by considering the following ("Good Samaritan") case. It seems true that the starving and poor ought to be fed. But that the starving and poor are fed implies that there are starving and poor. By basic principles of SDL we can infer that there ought to be starving and poor! The argument is due to the basic K axiom of SDL together with the following principle valid in any normal modal logic
:
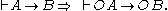
If we introduce an intensional conditional operator then we can say that the starving ought to be fed only on the condition that there are in fact starving: in symbols O(A/B). But then the following argument fails on the usual (e.g. Lewis 73) semantics for conditionals: from O(A/B) and that A implies B, infer OB.
Indeed one might define the unary operator O in terms of the binary conditional one O(A/B) as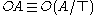
, where 
stands for an arbitrary tautology
of the underlying logic (which, in the case of SDL, is classical). Similarly Alan R. Anderson (1959) shows how to define O in terms of the alethic operator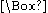
and a deontic constant (i.e. 0-ary modal operator) s standing for some sanction (i.e. bad thing, prohibition, etc.): 
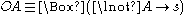. Intuitively, the right side of the biconditional says that A's failing to hold necessarily (or strictly) implies a sanction.
Under the first representation it is vacuously true that if you commit a forbidden act, then you ought to commit any other act, regardless of whether that second act was obligatory, permitted or forbidden (Von Wright 1956, cited in Aqvist 1994). Under the second representation, we are vulnerable to the gentle murder paradox, where the plausible statements (1) if you murder, you ought to murder gently, (2) you do commit murder, and (3) to murder gently you must murder imply the less plausible statement: you ought to murder.
Some deontic logicians have responded to this problem by developing dyadic deontic logics, which contain binary deontic operators:
(The notation is modeled on that used to represent conditional probability
.) Dyadic deontic logic escapes some of the problems of standard (unary) deontic logic, but it is subject to some problems of its own.
deontic logics, paraconsistent
deontic logics, and dynamic
deontic logics.
cannot be true or false, but truth and truth values seem essential to logic. There are two possible answers:
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
that is concerned with obligation
Obligation
An obligation is a requirement to take some course of action, whether legal or moral. There are also obligations in other normative contexts, such as obligations of etiquette, social obligations, and possibly...
, permission
Permission
Permission, in philosophy, is the attribute of a person whose performance of a specific action, otherwise ethically wrong or dubious, would thereby involve no ethical fault. The term "permission" is more commonly used to refer to consent...
, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. Typically, a deontic logic uses OA to mean it is obligatory that A, (or it ought to be (the case) that A), and PA to mean it is permitted (or permissible) that A. The term deontic is derived from the ancient Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
déon - δέον (gen.: δέοντος), meaning, roughly, that which is binding or proper.
Early Deontic Logic
Philosophers from the IndiaIndia
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n Mimamsa school
Mimamsa
' , a Sanskrit word meaning "investigation" , is the name of an astika school of Hindu philosophy whose primary enquiry is into the nature of dharma based on close hermeneutics of the Vedas...
to those of Ancient Greece
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
have remarked on the formal logical relations of deontic concepts and philosophers from the late Middle Ages
Medieval philosophy
Medieval philosophy is the philosophy in the era now known as medieval or the Middle Ages, the period roughly extending from the fall of the Western Roman Empire in the fifth century AD to the Renaissance in the sixteenth century...
compared deontic concepts with alethic ones. In his Elementa juris naturalis, Leibniz notes the logical relations between the licitum, illicitum, debitum, and indifferens are equivalent to those between the possible, impossible, necessarium, and contingens respectively.
Mally's First Deontic Logic and von Wright's First Plausible Deontic Logic
Ernst MallyErnst Mally
Ernst Mally was an Austrian philosopher affiliated with the so-called Graz School of phenomenology. A pupil of Alexius Meinong, he was one of the founders of deontic logic and is mainly known for his contributions in that field of research.- Life :Mally was born in the town of Kranj in the Duchy...
, a pupil of Alexius Meinong
Alexius Meinong
Alexius Meinong was an Austrian philosopher, a realist known for his unique ontology...
, was the first to propose a formal system of deontic logic in his Grundgesetze des Sollens and he founded it on the syntax of Whitehead's and Russell's propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
. Mally's deontic vocabulary consisted of the logical constants U and ∩, unary connective !, and binary connectives f and ∞.
- * Mally read !A as "A ought to be the case".
* He read A f B as "A requires B" .
* He read A ∞ B as "A and B require each other."
* He read U as "the unconditionally obligatory" .
* He read ∩ as "the unconditionally forbidden".
Mally defined f, ∞, and ∩ as follows:
- Def. f. A f B = A → !B
Def. ∞. A ∞ B = (A f B) & (B f A)
Def. ∩. ∩ = ¬U
Mally proposed five informal principles:
- (i) If A requires B and if B requires C, then A requires C.
(ii) If A requires B and if A requires C, then A requires B and C.
(iii) A requires B if and only if it is obligatory that if A then B.
(iv) The unconditionally obligatory is obligatory.
(v) The unconditionally obligatory does not require its own negation.
He formalized these principles and took them as his axioms:
- I. ((A f B) & (B → C)) → (A f C)
II. ((A f B) & (A f C)) → (A f (B & C))
III. (A f B) ↔ !(A → B)
IV. ∃U !U
V. ¬(U f ∩)
From these axioms Mally deduced 35 theorems, many of which he rightly considered strange. Karl Menger
Karl Menger
Karl Menger was a mathematician. He was the son of the famous economist Carl Menger. He is credited with Menger's theorem. He worked on mathematics of algebras, algebra of geometries, curve and dimension theory, etc...
showed that !A ↔ A is a theorem and thus that the introduction of the ! sign is irrelevant and that A ought to be the case if A is the case. After Menger, philosophers no longer considered Mally's system viable. Gert Lokhorst lists Mally's 35 theorems and gives a proof for Menger's theorem at the Stanford Encyclopedia of Philosophy under Mally's Deontic Logic.
The first plausible system of deontic logic was proposed by G. H. von Wright
Georg Henrik von Wright
Georg Henrik von Wright was a Finnish philosopher, who succeeded Ludwig Wittgenstein as professor at the University of Cambridge. He published in English, Finnish, German, and in Swedish. Belonging to the Swedish-speaking minority of Finland, von Wright also had Finnish and 17th-century Scottish...
in his paper Deontic Logic in the philosophical journal Mind in 1951. (Von Wright was also the first to use the term "deontic" in English to refer to this kind of logic although Mally published the German paper Deontik in 1926.) Since the publication of von Wright's seminal paper, many philosophers and computer scientists have investigated and developed systems of deontic logic. Nevertheless, to this day deontic logic remains one of the most controversial and least agreed-upon areas of logic.
G. H. von Wright did not base his 1951 deontic logic on the syntax of the propositional calculus as Mally had done, but was instead influenced by alethic modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s, which Mally had not benefited from. In 1964, von Wright published A New System of Deontic Logic, which was a return to the syntax of the propositional calculus and thus a significant return to Mally's system. (For more on von Wright's departure from and return to the syntax of the propositional calculus, see Deontic Logic: A Personal View and A New System of Deontic Logic, both by Georg Henrik von Wright.) G. H. von Wright's adoption of the modal logic of possibility and necessity for the purposes of normative reasoning was a return to Leibniz.
Standard deontic logic
In von Wright's first system, obligatoriness and permissibility were treated as features of acts. It was found not much later that a deontic logic of propositions could be given a simple and elegant Kripke-style semanticsKripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
, and von Wright himself joined this movement. The deontic logic so specified came to be known as "standard deontic logic," often referred to as SDL, KD, or simply D. It can be axiomatized by adding the following axioms to a standard axiomatization of classical propositional logic:
In English, these axioms say, respectively:
- If it ought to be that A implies B, then if it ought to be that A, it ought to be that B;
- If A is permissible, then it is not the case that it ought not to be that A.
FA, meaning it is forbidden that A, can be defined (equivalently) as
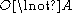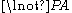or .There are two main extensions of SDL that are usually considered. The first results by adding an alethic modal operator
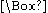in order to express the Kantian claim that "ought implies can":
where
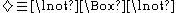. It is generally assumed that is at least a KT operator, but most commonly it is taken to be an S5 operator.The other main extension results by adding a "conditional obligation" operator O(A/B) read "It is obligatory that A given (or conditional on) B". Motivation for a conditional operator is given by considering the following ("Good Samaritan") case. It seems true that the starving and poor ought to be fed. But that the starving and poor are fed implies that there are starving and poor. By basic principles of SDL we can infer that there ought to be starving and poor! The argument is due to the basic K axiom of SDL together with the following principle valid in any normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
:
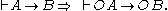
If we introduce an intensional conditional operator then we can say that the starving ought to be fed only on the condition that there are in fact starving: in symbols O(A/B). But then the following argument fails on the usual (e.g. Lewis 73) semantics for conditionals: from O(A/B) and that A implies B, infer OB.
Indeed one might define the unary operator O in terms of the binary conditional one O(A/B) as
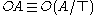, where stands for an arbitrary tautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
of the underlying logic (which, in the case of SDL, is classical). Similarly Alan R. Anderson (1959) shows how to define O in terms of the alethic operator
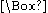and a deontic constant (i.e. 0-ary modal operator) s standing for some sanction (i.e. bad thing, prohibition, etc.): 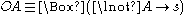. Intuitively, the right side of the biconditional says that A's failing to hold necessarily (or strictly) implies a sanction.Dyadic deontic logic
An important problem of deontic logic is that of how to properly represent conditional obligations, e.g. If you smoke (s), then you ought to use an ashtray (a). It is not clear that either of the following representations is adequate:
Under the first representation it is vacuously true that if you commit a forbidden act, then you ought to commit any other act, regardless of whether that second act was obligatory, permitted or forbidden (Von Wright 1956, cited in Aqvist 1994). Under the second representation, we are vulnerable to the gentle murder paradox, where the plausible statements (1) if you murder, you ought to murder gently, (2) you do commit murder, and (3) to murder gently you must murder imply the less plausible statement: you ought to murder.
Some deontic logicians have responded to this problem by developing dyadic deontic logics, which contain binary deontic operators:
-
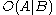means it is obligatory that A, given B -
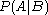means it is permissible that A, given B.
(The notation is modeled on that used to represent conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
.) Dyadic deontic logic escapes some of the problems of standard (unary) deontic logic, but it is subject to some problems of its own.
Other variations
Many other varieties of deontic logic have been developed, including non-monotonicNon-monotonic logic
A non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a...
deontic logics, paraconsistent
Paraconsistent logic
A paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
deontic logics, and dynamic
Dynamic logic (modal logic)
Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
deontic logics.
Jørgensen's Dilemma
Deontic logic faces Jørgensen's Dilemma. NormsNorm (philosophy)
Norms are concepts of practical import, oriented to effecting an action, rather than conceptual abstractions that describe, explain, and express. Normative sentences imply “ought-to” types of statements and assertions, in distinction to sentences that provide “is” types of statements and assertions...
cannot be true or false, but truth and truth values seem essential to logic. There are two possible answers:
- Deontic logic handles norm propositionPropositionIn logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, not norms; - There might be alternative concepts to truth, e.g. validityValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
or success, as it is defined in speech actSpeech actSpeech Act is a technical term in linguistics and the philosophy of language. The contemporary use of the term goes back to John L. Austin's doctrine of locutionary, illocutionary, and perlocutionary acts...
theory.
See also
- Modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
- Imperative logicImperative logicImperative logic is the field of logic concerned with arguments containing sentences in the imperative mood. In contrast to sentences in the declarative mood, imperatives are neither true nor false. This leads to a number of logical dilemmas, puzzles, and paradoxes...
- Norm (philosophy)Norm (philosophy)Norms are concepts of practical import, oriented to effecting an action, rather than conceptual abstractions that describe, explain, and express. Normative sentences imply “ought-to” types of statements and assertions, in distinction to sentences that provide “is” types of statements and assertions...
- KED
Resources
- Lennart ÅqvistLennart ÅqvistLennart Åqvist is a Swedish logician. He was a founding member of the editorial board of the Journal of Philosophical Logic....
, 1994, "Deontic Logic" in D. Gabbay and F. Guenthner, ed., Handbook of Philosophical Logic: Volume II Extensions of Classical Logic. Kluwer. - Hilpinen, Risto, 2001, "Deontic Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- G. H. von Wright, 1951. "Deontic logic," Mind 60: 1-15.
External links
- McNamara, Deontic Logic, Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
, 2006. - Lokhorst, Mally's Deontic Logic, Stanford Encyclopedia of Philosophy, 2004.