
Modal algebra
Encyclopedia
In algebra
and logic
, a modal algebra is a structure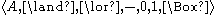 such that
such that
Modal algebras provide models of propositional modal logic
s in the same way as Boolean algebras are models of classical logic
. In particular, the variety
of all modal algebras is the equivalent algebraic semantics of the modal logic K in the sense of abstract algebraic logic
, and the lattice
of its subvarieties is dually isomorphic to the lattice of normal modal logic
s.
Stone's representation theorem can be generalized to the Jónsson–Tarski duality, which ensures that each modal algebra can be represented
as the algebra of admissible sets in a modal general frame
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a modal algebra is a structure
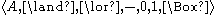 such that
such that
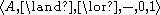 is a Boolean algebra,
is a Boolean algebra, is a unary operation on A satisfying
is a unary operation on A satisfying 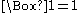 and
and 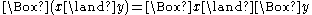 for all x, y in A.
for all x, y in A.
Modal algebras provide models of propositional modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s in the same way as Boolean algebras are models of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
. In particular, the variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of all modal algebras is the equivalent algebraic semantics of the modal logic K in the sense of abstract algebraic logic
Abstract Algebraic Logic
In mathematical logic, abstract algebraic logic is the study of the algebraization of deductive systemsarising as an abstraction of the well-known Lindenbaum-Tarski algebra, and how the resulting algebras are related to logical systems.-Overview:...
, and the lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of its subvarieties is dually isomorphic to the lattice of normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
s.
Stone's representation theorem can be generalized to the Jónsson–Tarski duality, which ensures that each modal algebra can be represented
Representation theorem
In mathematics, a representation theorem is a theorem that states that every abstract structure with certain properties is isomorphic to a concrete structure.For example,*in algebra,...
as the algebra of admissible sets in a modal general frame
General frame
In logic, general frames are Kripke frames with an additional structure, which are used to model modal and intermediate logics...
.

