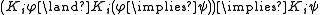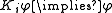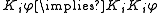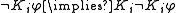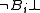Epistemic logic
Encyclopedia
Epistemic modal logic is a subfield of modal logic
that is concerned with reasoning about knowledge
. While epistemology has a long philosophical tradition dating back to Ancient Greece
, epistemic logic is a much more recent development with applications in many fields, including philosophy
, theoretical computer science
, artificial intelligence
, economics
and linguistics
. While philosophers since Aristotle
have discussed modal logic, and Medieval philosophers
such as Ockham
and Duns Scotus
developed many of their observations, it was C.I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Kripke
.
's paper An Essay in Modal Logic from 1951 that is seen as a founding document. It was not until 1962 that another Finn, Hintikka
, would write Knowledge and Belief, the first book-length work to suggest using modalities to capture the semantics of knowledge rather than the alethic statements typically discussed in modal logic. This work laid much of the groundwork for the subject, but a great deal of research has taken place since that time. For example, epistemic logic has been combined recently with some ideas from dynamic logic
to create public announcement logic and product update logic, which attempt to model the epistemic subtleties of conversations. The seminal works in this field are by Plaza, van Benthem
, and Baltag, Moss, and Solecki.
s model. In order to do this, we must divide the set of possible worlds between those that are compatible with an agent's knowledge, and those that are not. This generally conforms with common usage. If I know that it is either Friday or Saturday, then I know for sure that it is not Thursday. There is no possible world compatible with my knowledge where it is Thursday, since in all these worlds it is either Friday or Saturday. While we will primarily be discussing the logic-based approach to accomplishing this task, it is worthwhile to mention here the other primary method in use, the event
-based approach. In this particular usage, events are sets of possible worlds, and knowledge is an operator on events. Though the strategies are closely related, there are two important distinctions to be made between them:
Typically, the logic-based approach has been used in fields such as philosophy, logic and AI, while the event-based approach is more often used in fields such as game theory
and mathematical economics
. In the logic-based approach, a syntax and semantics have been built using the language of modal logic, which we will now describe.
of epistemic logic, usually written K, can be read as "it is known that," "it is epistemically necessary that," or "it is inconsistent with what is known that not." If there is more than one agent whose knowledge is to be represented, subscripts can be attached to the operator (
, 
, etc.) to indicate which agent one is talking about. So 
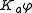can be read as "Agent 
knows that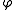 
." Thus, epistemic logic can be an example of multimodal logic
applied for knowledge representation
. The dual of K, which would be in the same relationship to K as
is to 
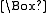, has no specific symbol, but can be represented by 
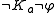, which can be read as "
does not know that not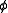 
" or "It is consistent with 
's knowledge that 
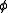is possible". The statement "
does not know whether or not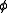 
" can be expressed as 
.
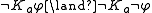In order to accommodate notions of common knowledge
and distributed knowledge
, three other modal operators can be added to the language. These are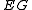
, which reads "every agent in group G knows;" 
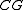, which reads "it is common knowledge to every agent in G;" and 
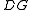, which reads "it is distributed knowledge to every agent in G." If 
is a formula of our language, then so are 
, 
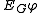, and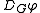 
. Just as the subscript after 
can be omitted when there is only one agent, the subscript after the modal operators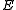 
, 
, and 
can be omitted when the group is the set of all agents.
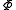is a triple 
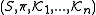, where S is a nonempty set of states or possible worlds, 
is an interpretation which associates with each state in S a truth assignment to the primitive propositions in 
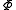, and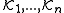 
are binary relation
s on S for n numbers of agents. It is important here not to confuse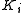
, our modal operator, and 
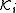, our accessibility relation.
The truth assignment tells us whether or not a proposition p is true or false in a certain state. So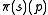
tells us whether p is true in state s in model 
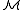. Truth depends not only on the structure, but on the current world as well. Just because something is true in one world does not mean it is true in another. To state that a formula 
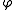is true at a certain world, one writes 
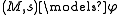, normally read as "
is true at (M,s)," or "(M,s) satisfies 
".
It is useful to think of our binary relation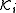
as a possibility relation, because it is meant to capture what worlds or states agent i considers to be possible. In idealized accounts of knowledge (e.g., describing the epistemic status of perfect reasoners with infinite memory capacity), it makes sense for 
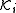to be an equivalence relation
, since this is the strongest form and is the most appropriate for the greatest number of applications. An equivalence relation is a binary relation that is reflexive
, symmetric
, and transitive
. The accessibility relation does not have to have these qualities; there are certainly other choices possible, such as those used when modeling belief rather than knowledge.
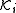is an equivalence relation, and that the agents are perfect reasoners, a few properties of knowledge can be derived. The properties listed here are often known as the "S5 Properties," for reasons described in the Axiom Systems section below.
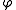and knows that 
, then the agent must also know 
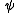. So,
is valid, then 
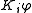. It does not mean that if 
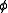is true, that agent i knows 
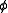. What it means is that if 
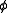is true in every world that an agent considers to be a possible world, then the agent must know 
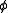at every possible world. This principle is traditionally called N.
has argued against its inclusion forcefully in his book, Knowledge and Its Limits.
. This is why the properties of knowledge described above are often called the S5 Properties.
Epistemic logic also deals with belief, not just knowledge. The basic modal operator is usually written B instead of K. In this case though, the knowledge axiom no longer seems right—agents only sometimes believe the truth—so it is usually replaced with the Consistency Axiom, traditionally called D:
which states that the agent does not believe a contradiction, or that which is false. When D replaces T in S5, the resulting system is known as KD45. This results in different properties for
as well. For example, in a system where an agent "believes" something to be true, but it is not actually true, the accessibility relation would be non-reflexive. The logic of belief is called doxastic logic.
is a logical consequence of 
, then there is no possible world where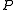 
is true but 
is not. So if a knows that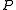 
, it follows that all of the logical consequences of 
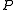are true of all of the possible worlds compatible with a 's beliefs. Therefore, a knows 
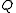. It is not epistemically possible for a that not-
given his knowledge that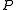 
. This consideration was a part of what led Robert Stalnaker
to develop two dimensionalism
, which can arguably explain how we might not know all the logical consequences of our beliefs even if there are no worlds where the propositions we know come out true but their consequences false.
Even when we ignore possible world semantics and stick to axiomatic systems, this peculiar feature holds. With K and N (the Distribution Rule and the Knowledge Generalization Rule, respectively), which are axioms that are minimally true of all modal logics, we can prove that we know all the logical consequences of our beliefs. If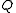
is a logical consequence of 
, then we can derive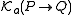 
with N and the conditional proof
and then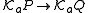
with K. When we translate this into epistemic terms, this says that if 
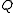is a logical consequence of 
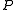, then a knows that it is, and if a knows 
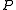, a knows 
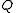. That is to say, a knows all the logical consequences of every proposition. This is necessarily true of all classical modal logics. But then, for example, if a knows that prime numbers are divisible only by themselves and the number one, then a knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, when a knows the definition of a prime number, a knows that this number is prime. It should be clear at this point that a is not human. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
that is concerned with reasoning about knowledge
Knowledge
Knowledge is a familiarity with someone or something unknown, which can include information, facts, descriptions, or skills acquired through experience or education. It can refer to the theoretical or practical understanding of a subject...
. While epistemology has a long philosophical tradition dating back to Ancient Greece
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
, epistemic logic is a much more recent development with applications in many fields, including philosophy
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
. While philosophers since Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
have discussed modal logic, and Medieval philosophers
Medieval philosophy
Medieval philosophy is the philosophy in the era now known as medieval or the Middle Ages, the period roughly extending from the fall of the Western Roman Empire in the fifth century AD to the Renaissance in the sixteenth century...
such as Ockham
William of Ockham
William of Ockham was an English Franciscan friar and scholastic philosopher, who is believed to have been born in Ockham, a small village in Surrey. He is considered to be one of the major figures of medieval thought and was at the centre of the major intellectual and political controversies of...
and Duns Scotus
Duns Scotus
Blessed John Duns Scotus, O.F.M. was one of the more important theologians and philosophers of the High Middle Ages. He was nicknamed Doctor Subtilis for his penetrating and subtle manner of thought....
developed many of their observations, it was C.I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
.
Historical development
Many papers were written in the fifties that spoke of a logic of knowledge in passing, but it was Finnish philosopher von WrightGeorg Henrik von Wright
Georg Henrik von Wright was a Finnish philosopher, who succeeded Ludwig Wittgenstein as professor at the University of Cambridge. He published in English, Finnish, German, and in Swedish. Belonging to the Swedish-speaking minority of Finland, von Wright also had Finnish and 17th-century Scottish...
's paper An Essay in Modal Logic from 1951 that is seen as a founding document. It was not until 1962 that another Finn, Hintikka
Jaakko Hintikka
Kaarlo Jaakko Juhani Hintikka is a Finnish philosopher and logician.Hintikka was born in Vantaa. After teaching for a number of years at Florida State University, Stanford, University of Helsinki, and the Academy of Finland, he is currently Professor of Philosophy at Boston University...
, would write Knowledge and Belief, the first book-length work to suggest using modalities to capture the semantics of knowledge rather than the alethic statements typically discussed in modal logic. This work laid much of the groundwork for the subject, but a great deal of research has taken place since that time. For example, epistemic logic has been combined recently with some ideas from dynamic logic
Dynamic logic (modal logic)
Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
to create public announcement logic and product update logic, which attempt to model the epistemic subtleties of conversations. The seminal works in this field are by Plaza, van Benthem
Johan van Benthem (logician)
Johannes Franciscus Abraham Karel van Benthem is a University Professor of logic at the University of Amsterdam at the Institute for Logic, Language and Computation and professor of philosophy at Stanford University . He was awarded the Spinozapremie in 1996.He studied physics , philosophy...
, and Baltag, Moss, and Solecki.
Standard possible worlds model
Most attempts at modeling knowledge have been based on the possible worldPossible world
In philosophy and logic, the concept of a possible world is used to express modal claims. The concept of possible worlds is common in contemporary philosophical discourse and has also been disputed.- Possibility, necessity, and contingency :...
s model. In order to do this, we must divide the set of possible worlds between those that are compatible with an agent's knowledge, and those that are not. This generally conforms with common usage. If I know that it is either Friday or Saturday, then I know for sure that it is not Thursday. There is no possible world compatible with my knowledge where it is Thursday, since in all these worlds it is either Friday or Saturday. While we will primarily be discussing the logic-based approach to accomplishing this task, it is worthwhile to mention here the other primary method in use, the event
Event (philosophy)
In philosophy, events are objects in time or instantiations of properties in objects. However, a definite definition has not been reached, as multiple theories exist concerning events.-Kim’s Property-Exemplification Account of Events:...
-based approach. In this particular usage, events are sets of possible worlds, and knowledge is an operator on events. Though the strategies are closely related, there are two important distinctions to be made between them:
- The underlying mathematical model of the logic-based approach are Kripke structureKripke structureA Kripke structure is a type of nondeterministic finite state machine proposed by Saul Kripke , used in model checking to represent the behavior of a system.It is a simple abstract machine to capture an idea of a computing machine,...
s, while the event-based approach employs the related Aumann structures. - In the event-based approach logical formulas are done away with completely, while the logic-based approach uses the system of modal logic.
Typically, the logic-based approach has been used in fields such as philosophy, logic and AI, while the event-based approach is more often used in fields such as game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and mathematical economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
. In the logic-based approach, a syntax and semantics have been built using the language of modal logic, which we will now describe.
Syntax
The basic modal operatorModal operator
In modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...
of epistemic logic, usually written K, can be read as "it is known that," "it is epistemically necessary that," or "it is inconsistent with what is known that not." If there is more than one agent whose knowledge is to be represented, subscripts can be attached to the operator (
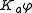, , etc.) to indicate which agent one is talking about. So can be read as "Agent knows that 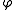." Thus, epistemic logic can be an example of multimodal logicMultimodal logic
A multimodal logic is a modal logic that has more than one primitive modal operator. They find substantial applications in theoretical computer science....
applied for knowledge representation
Knowledge representation
Knowledge representation is an area of artificial intelligence research aimed at representing knowledge in symbols to facilitate inferencing from those knowledge elements, creating new elements of knowledge...
. The dual of K, which would be in the same relationship to K as
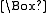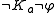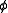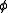is to , has no specific symbol, but can be represented by , which can be read as " does not know that not " or "It is consistent with 's knowledge that is possible". The statement " does not know whether or not 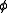" can be expressed as 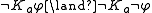.In order to accommodate notions of common knowledge
Common knowledge (logic)
Common knowledge is a special kind of knowledge for a group of agents. There is common knowledge of p in a group of agents G when all the agents in G know p, they all know that they know p, they all know that they all know that they know p, and so on ad infinitum.The concept was first introduced in...
and distributed knowledge
Distributed knowledge
Distributed knowledge is a term used in multi-agent system research that refers to all the knowledge that a community of agents possesses and might apply in solving a problem. Distributed knowledge is approximately what "a wise man knows" or what someone who has complete knowledge of what each...
, three other modal operators can be added to the language. These are
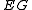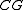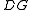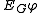, which reads "every agent in group G knows;" , which reads "it is common knowledge to every agent in G;" and , which reads "it is distributed knowledge to every agent in G." If is a formula of our language, then so are , , and 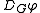. Just as the subscript after can be omitted when there is only one agent, the subscript after the modal operators 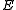, , and can be omitted when the group is the set of all agents.Semantics
As we mentioned above, the logic-based approach is built upon the possible worlds model, the semantics of which are often given definite form in Kripke structures, also known as Kripke models. 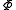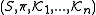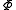A Kripke structure M for n agents over is a triple , where S is a nonempty set of states or possible worlds, is an interpretation which associates with each state in S a truth assignment to the primitive propositions in , and 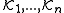are binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s on S for n numbers of agents. It is important here not to confuse
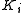, our modal operator, and 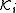, our accessibility relation.The truth assignment tells us whether or not a proposition p is true or false in a certain state. So
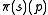tells us whether p is true in state s in model 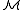. Truth depends not only on the structure, but on the current world as well. Just because something is true in one world does not mean it is true in another. To state that a formula 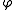is true at a certain world, one writes 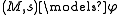, normally read as " is true at (M,s)," or "(M,s) satisfies ".It is useful to think of our binary relation
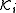as a possibility relation, because it is meant to capture what worlds or states agent i considers to be possible. In idealized accounts of knowledge (e.g., describing the epistemic status of perfect reasoners with infinite memory capacity), it makes sense for 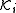to be an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, since this is the strongest form and is the most appropriate for the greatest number of applications. An equivalence relation is a binary relation that is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
. The accessibility relation does not have to have these qualities; there are certainly other choices possible, such as those used when modeling belief rather than knowledge.
The properties of knowledge
Assuming that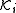 is an equivalence relation, and that the agents are perfect reasoners, a few properties of knowledge can be derived. The properties listed here are often known as the "S5 Properties," for reasons described in the Axiom Systems section below.The distribution axiom
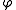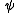This axiom is traditionally known as K. In epistemic terms, it states that if an agent knows and knows that , then the agent must also know . So,
The knowledge generalization rule
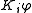Another property we can derive is that if is valid, then . It does not mean that if 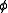is true, that agent i knows 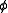. What it means is that if 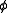is true in every world that an agent considers to be a possible world, then the agent must know 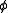at every possible world. This principle is traditionally called N.
The knowledge or truth axiom
This axiom is also known as T. It says that if an agent knows facts, the facts must be true. This has often been taken as the major distinguishing feature between knowledge and belief. We can believe a statement to be true when it is false, but it would be impossible to know a false statement.
The positive introspection axiom
This property and the next state that an agent has introspection about its own knowledge, and are traditionally known as 4 and 5, respectively. The Positive Introspection Axiom, also known as the KK Axiom, says specifically that agents know that they know what they know. This axiom may seem less obvious than the ones listed previously, and Timothy WilliamsonTimothy Williamson
Timothy Williamson is a British philosopher whose main research interests are in philosophical logic, philosophy of language, epistemology and metaphysics....
has argued against its inclusion forcefully in his book, Knowledge and Its Limits.
The negative introspection axiom
The Negative Introspection Axiom says that agents know that they do not know what they do not know.
Axiom systems
Different modal logics can be derived from taking different subsets of these axioms, and these logics are normally named after the important axioms being employed. However, this is not always the case. KT45, the modal logic that results from the combining of K, T, 4, 5, and the Knowledge Generalization Rule, is primarily known as S5S5 (modal logic)
In logic and philosophy, S5 is one of five systems of modal logic proposed byClarence Irving Lewis and Cooper Harold Langford in their 1932 book Symbolic Logic.It is a normal modal logic, and one of the oldest systems of modal logic of any kind....
. This is why the properties of knowledge described above are often called the S5 Properties.
Epistemic logic also deals with belief, not just knowledge. The basic modal operator is usually written B instead of K. In this case though, the knowledge axiom no longer seems right—agents only sometimes believe the truth—so it is usually replaced with the Consistency Axiom, traditionally called D:
which states that the agent does not believe a contradiction, or that which is false. When D replaces T in S5, the resulting system is known as KD45. This results in different properties for
as well. For example, in a system where an agent "believes" something to be true, but it is not actually true, the accessibility relation would be non-reflexive. The logic of belief is called doxastic logic.Problems with the possible world model and with the modal model of knowledge
If we take the possible worlds approach to knowledge, it follows that our epistemic agent a knows all the logical consequences of his or her or its beliefs. If is a logical consequence of , then there is no possible world where 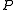is true but is not. So if a knows that 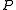, it follows that all of the logical consequences of 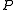are true of all of the possible worlds compatible with a 's beliefs. Therefore, a knows 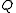. It is not epistemically possible for a that not- given his knowledge that 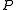. This consideration was a part of what led Robert StalnakerRobert Stalnaker
Robert C. Stalnaker is Laurance S. Rockefeller Professor of Philosophy at the Massachusetts Institute of Technology. In 2007, he delivered the John Locke Lectures at Oxford University on the topic of Our Knowledge of the Internal World...
to develop two dimensionalism
Two dimensionalism
Two-dimensionalism is an approach to semantics in analytic philosophy. It is a theory of how to determine the sense and reference of a word and the truth-value of a sentence...
, which can arguably explain how we might not know all the logical consequences of our beliefs even if there are no worlds where the propositions we know come out true but their consequences false.
Even when we ignore possible world semantics and stick to axiomatic systems, this peculiar feature holds. With K and N (the Distribution Rule and the Knowledge Generalization Rule, respectively), which are axioms that are minimally true of all modal logics, we can prove that we know all the logical consequences of our beliefs. If
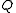is a logical consequence of , then we can derive 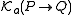with N and the conditional proofConditional proof
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent....
and then
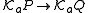with K. When we translate this into epistemic terms, this says that if 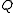is a logical consequence of 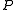, then a knows that it is, and if a knows 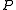, a knows 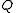. That is to say, a knows all the logical consequences of every proposition. This is necessarily true of all classical modal logics. But then, for example, if a knows that prime numbers are divisible only by themselves and the number one, then a knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, when a knows the definition of a prime number, a knows that this number is prime. It should be clear at this point that a is not human. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).See also
- Epistemology
- Modal LogicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
- Common knowledgeCommon knowledge (logic)Common knowledge is a special kind of knowledge for a group of agents. There is common knowledge of p in a group of agents G when all the agents in G know p, they all know that they know p, they all know that they all know that they know p, and so on ad infinitum.The concept was first introduced in...
- Logic in computer science
- Closure (philosophy)Closure (philosophy)Closure, in epistemology, is the principle that if a subject S knows that p, and S knows that p entails q, then S can thereby come to know that q. Most epistemological theories involve a closure principle and many sceptical arguments assume a closure principle, arguing for instance that if you...
- Philosophical ExplanationsPhilosophical explanationsPhilosophical Explanations is a wide-ranging metaphysical, epistemological, and ethical treatise written by Robert Nozick and published in 1981.-The Parthenon Model and non-coercive philosophy:...
- Two dimensionalismTwo dimensionalismTwo-dimensionalism is an approach to semantics in analytic philosophy. It is a theory of how to determine the sense and reference of a word and the truth-value of a sentence...
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- "Epistemic Logic" -- Hendricks, Vincent and John Symons
- "Modal logic" -- by James Garson.
- "Common Knowledge" -- Vanderschraaf, Peter.
- "Epistemic modal logic" -- Ho Ngoc Duc.