
Predicate logic
Encyclopedia
In mathematical logic
, predicate logic is the generic term for symbolic formal system
s like first-order logic
, second-order logic
, many-sorted logic
or infinitary logic
. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified
. Two common quantifiers are the existential
∃ ("there exists") and universal
∀ ("for all") quantifiers. The variables could be elements in the universe under discussion
, or perhaps relations or functions over that universe. For instance, an existential quantifier over a function symbol would be interpreted as modifier "there is a function".
In informal usage, the term "predicate logic" occasionally refers to first-order logic
. Some authors consider the predicate calculus to be an axiomatized form of predicate logic, and the predicate logic to be derived from an informal, more intuitive development.
Predicate logics also include logics mixing modal operators and quantifiers. See Modal logic
, Saul Kripke
, Barcan Marcus
formulae, A. N. Prior and Nicholas Rescher
.
A function expression is a function symbol followed by its arguments. The arguments are elements from the domain of the function; the number of arguments is equal to the arity of the function. The arguments are enclosed in parentheses and separated by commas. e.g.:
are all well-formed function expressions.
Predicate logics may be viewed syntactically as Chomsky
grammars. As such, predicate logics (as well as modal logics and mixed modal predicate logics) may be viewed as context-sensitive, or more typically as context-free, grammars. As each one of the four Chomsky-type grammars have equivalent automata
, these logics can be viewed as automata just as well.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, predicate logic is the generic term for symbolic formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s like first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
, many-sorted logic
Many-sorted logic
Many-sorted logic can reflect formally our intention, not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming...
or infinitary logic
Infinitary logic
An infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
. Two common quantifiers are the existential
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
∃ ("there exists") and universal
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
∀ ("for all") quantifiers. The variables could be elements in the universe under discussion
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
, or perhaps relations or functions over that universe. For instance, an existential quantifier over a function symbol would be interpreted as modifier "there is a function".
In informal usage, the term "predicate logic" occasionally refers to first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. Some authors consider the predicate calculus to be an axiomatized form of predicate logic, and the predicate logic to be derived from an informal, more intuitive development.
Predicate logics also include logics mixing modal operators and quantifiers. See Modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
, Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
, Barcan Marcus
Ruth Barcan Marcus
Ruth Barcan Marcus is the American philosopher and logician after whom the Barcan formula is named. She is a pioneering figure in the quantification of modal logic and the theory of direct reference...
formulae, A. N. Prior and Nicholas Rescher
Nicholas Rescher
Nicholas Rescher is an American philosopher at the University of Pittsburgh. In a productive research career extending over six decades, Rescher has established himself as a systematic philosopher of the old style and author of a system of pragmatic idealism which weaves together threads of...
.
Syntax
Predicate calculus symbols may represent either variables, constants, functions or predicates.- Constants name specific objects or properties in the domain of discourseDomain of discourseIn the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
. Thus George, tree, tall and blue are examples of well formed constant symbols. The constants (true) and
(true) and 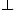 (false) are sometimes included.
(false) are sometimes included. - Variable symbols are used to designate general classes or objects or properties in the domain of discourse.
- Functions denote a mapping of one or more elements in a set(called the domain of the function) into a unique element of another set(the range of the function). Elements of the domain and range are objects in the world of discourse. Every function symbol has an associated arity, indicating the number of elements in the domain mapped onto each element of range.
A function expression is a function symbol followed by its arguments. The arguments are elements from the domain of the function; the number of arguments is equal to the arity of the function. The arguments are enclosed in parentheses and separated by commas. e.g.:
- f(X,Y)
- father(david)
- price(apple)
are all well-formed function expressions.
Predicate logics may be viewed syntactically as Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
grammars. As such, predicate logics (as well as modal logics and mixed modal predicate logics) may be viewed as context-sensitive, or more typically as context-free, grammars. As each one of the four Chomsky-type grammars have equivalent automata
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
, these logics can be viewed as automata just as well.

