
Dynamic logic (modal logic)
Encyclopedia
Dynamic logic is an extension of modal logic
originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.
is characterized by the modal operator
s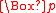 (box p) asserting that
(box p) asserting that  is necessarily the case, and
is necessarily the case, and  (diamond p) asserting that
(diamond p) asserting that  is possibly the case. Dynamic logic extends this by associating to every action
is possibly the case. Dynamic logic extends this by associating to every action  the modal operators
the modal operators  and
and  , thereby making it a multimodal logic
, thereby making it a multimodal logic
. The meaning of is that after performing action
is that after performing action  it is necessarily the case that
it is necessarily the case that  holds, that is,
holds, that is,  must bring about
must bring about  . The meaning of
. The meaning of 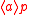 is that after performing
is that after performing  it is possible that
it is possible that 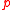 holds, that is,
holds, that is,  might bring about
might bring about 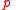 . These operators are related by
. These operators are related by  and
and  , analogously to the relationship between the universal (
, analogously to the relationship between the universal ( ) and existential (
) and existential ( ) quantifiers.
) quantifiers.
Dynamic logic permits compound actions built up from smaller actions. While the basic control operators of any programming language could be used for this purpose, Kleene's regular expression
operators are a good match to modal logic. Given actions and
and  , the compound action
, the compound action  , choice, also written
, choice, also written  or
or 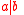 , is performed by performing one of
, is performed by performing one of  or
or  . The compound action
. The compound action  , sequence, is performed by performing first
, sequence, is performed by performing first  and then
and then  . The compound action
. The compound action  , iteration, is performed by performing
, iteration, is performed by performing  zero or more times, sequentially. The constant action
zero or more times, sequentially. The constant action  or BLOCK does nothing and does not terminate, whereas the constant action
or BLOCK does nothing and does not terminate, whereas the constant action 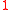 or SKIP or NOP, definable as
or SKIP or NOP, definable as  , does nothing but does terminate.
, does nothing but does terminate.
including such axioms for modal operators as the above-mentioned axiom and the two inference rules modus ponens (
and the two inference rules modus ponens (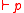 and
and 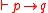 implies
implies 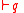 ) and necessitation (
) and necessitation (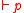 implies
implies  ).
).
A1.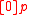
A2.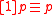
A3.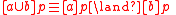
A4.
A5.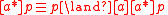
A6.
Axiom A1 makes the empty promise that when BLOCK terminates,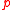 will hold, even if
will hold, even if  is the proposition false. (Thus BLOCK abstracts the essence of the action of hell freezing over.)
is the proposition false. (Thus BLOCK abstracts the essence of the action of hell freezing over.)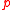 into itself.
into itself. or
or  must bring about
must bring about 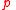 , then
, then  must bring about
must bring about 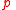 and likewise for
and likewise for  , and conversely.
, and conversely. and then
and then  must bring about
must bring about 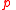 , then
, then  must bring about a situation in which
must bring about a situation in which  must bring about
must bring about  .
. of Kleene algebra
of Kleene algebra
.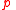 holds now, and no matter how often we perform
holds now, and no matter how often we perform  it remains the case that the truth of
it remains the case that the truth of 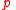 after that performance entails its truth after one more performance of
after that performance entails its truth after one more performance of  , then
, then 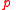 must remain true no matter how often we perform
must remain true no matter how often we perform  . A6 is recognizable as mathematical induction
. A6 is recognizable as mathematical induction
with the action n := n+1 of incrementing n generalized to arbitrary actions .
.
 permits the derivation of the following six theorems corresponding to the above:
permits the derivation of the following six theorems corresponding to the above:
T1.
T2.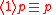
T3.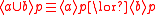
T4.
T5.
T6.
T1 asserts the impossibility of bringing anything about by performing BLOCK.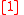 and
and  have the same force.
have the same force. or
or  could bring about
could bring about  , then either
, then either  or
or  alone could bring about
alone could bring about  .
. by performing
by performing  sufficiently often, then either
sufficiently often, then either 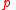 is true now or it is possible to perform
is true now or it is possible to perform  repeatedly to bring about a situation where
repeatedly to bring about a situation where 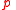 is (still) false but one more performance of
is (still) false but one more performance of  could bring about
could bring about 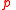 .
.
Box and diamond are entirely symmetric with regard to which one takes as primitive. An alternative axiomatization would have been to take the theorems T1-T6 as axioms, from which we could then have derived A1-A6 as theorems.
The difference between implication and inference is the same in dynamic logic as in any other logic: whereas the implication asserts that if
asserts that if 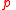 is true then so is
is true then so is  , the inference
, the inference  asserts that if
asserts that if 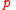 is valid then so is
is valid then so is  . However the dynamic nature of dynamic logic moves this distinction out of the realm of abstract axiomatics into the common-sense experience of situations in flux. The inference rule
. However the dynamic nature of dynamic logic moves this distinction out of the realm of abstract axiomatics into the common-sense experience of situations in flux. The inference rule  , for example, is sound because its premise asserts that
, for example, is sound because its premise asserts that 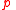 holds at all times, whence no matter where
holds at all times, whence no matter where  might take us,
might take us, 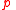 will be true there. The implication
will be true there. The implication 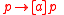 is not valid, however, because the truth of
is not valid, however, because the truth of 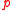 at the present moment is no guarantee of its truth after performing
at the present moment is no guarantee of its truth after performing  . For example,
. For example, 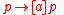 will be true in any situation where
will be true in any situation where 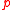 is false, or in any situation where
is false, or in any situation where 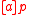 is true, but the assertion
is true, but the assertion 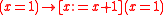 is false in any situation where
is false in any situation where  has value 1, and therefore is not valid.
has value 1, and therefore is not valid.
 for the action of kicking the TV, and
for the action of kicking the TV, and  for the proposition that the TV is broken, dynamic logic expresses this inference as
for the proposition that the TV is broken, dynamic logic expresses this inference as 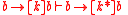 , having as premise
, having as premise 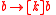 and as conclusion
and as conclusion 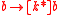 . The meaning of
. The meaning of  is that it is guaranteed that after kicking the TV, it is broken. Hence the premise
is that it is guaranteed that after kicking the TV, it is broken. Hence the premise 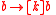 means that if the TV is broken, then after kicking it once it will still be broken.
means that if the TV is broken, then after kicking it once it will still be broken.  denotes the action of kicking the TV zero or more times. Hence the conclusion
denotes the action of kicking the TV zero or more times. Hence the conclusion  means that if the TV is broken, then after kicking it zero or more times it will still be broken. For if not, then after the second-to-last kick the TV would be in a state where kicking it once more would fix it, which the premise claims can never happen under any circumstances.
means that if the TV is broken, then after kicking it zero or more times it will still be broken. For if not, then after the second-to-last kick the TV would be in a state where kicking it once more would fix it, which the premise claims can never happen under any circumstances.
The inference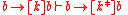 is sound. However the implication
is sound. However the implication  is not valid because we can easily find situations in which
is not valid because we can easily find situations in which 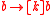 holds but
holds but 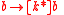 does not. In any such counterexample situation,
does not. In any such counterexample situation,  must hold but
must hold but  must be false, while
must be false, while 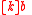 however must be true. But this could happen in any situation where the TV is broken but can be revived with two kicks. The implication fails (is not valid) because it only requires that
however must be true. But this could happen in any situation where the TV is broken but can be revived with two kicks. The implication fails (is not valid) because it only requires that 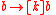 hold now, whereas the inference succeeds (is sound) because it requires that
hold now, whereas the inference succeeds (is sound) because it requires that 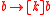 hold in all situations, not just the present one.
hold in all situations, not just the present one.
An example of a valid implication is the proposition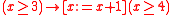 . This says that if
. This says that if  is greater or equal to 3, then after incrementing
is greater or equal to 3, then after incrementing  ,
,  must be greater or equal to 4. In the case of deterministic actions
must be greater or equal to 4. In the case of deterministic actions  that are guaranteed to terminate, such as
that are guaranteed to terminate, such as 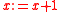 , must and might have the same force, that is,
, must and might have the same force, that is,  and
and  have the same meaning. Hence the above proposition is equivalent to
have the same meaning. Hence the above proposition is equivalent to 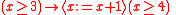 asserting that if
asserting that if  is greater or equal to 3 then after performing
is greater or equal to 3 then after performing  ,
,  might be greater or equal to 4.
might be greater or equal to 4.
 where
where  is a variable and
is a variable and  is an expression built from constants and variables with whatever operations are provided by the language, such as addition and multiplication. The Hoare axiom for assignment is not given as a single axiom but rather as an axiom schema.
is an expression built from constants and variables with whatever operations are provided by the language, such as addition and multiplication. The Hoare axiom for assignment is not given as a single axiom but rather as an axiom schema.
A7.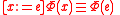
This is a schema in the sense that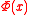 can be instantiated with any formula
can be instantiated with any formula  containing zero or more instances of a variable
containing zero or more instances of a variable  . The meaning of
. The meaning of 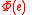 is
is  with those occurrences of
with those occurrences of  that occur free in
that occur free in  , i.e. not bound by some quantifier as in
, i.e. not bound by some quantifier as in 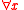 , replaced by
, replaced by  . For example we may instantiate A7 with
. For example we may instantiate A7 with 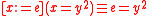 , or with
, or with  . Such an axiom schema allows infinitely many axioms having a common form to be written as a finite expression connoting that form.
. Such an axiom schema allows infinitely many axioms having a common form to be written as a finite expression connoting that form.
The instance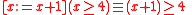 of A7 allows us to calculate mechanically that the example
of A7 allows us to calculate mechanically that the example 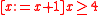 encountered a few paragraphs ago is equivalent to
encountered a few paragraphs ago is equivalent to 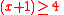 , which in turn is equivalent to
, which in turn is equivalent to  by elementary algebra
by elementary algebra
.
An example illustrating assignment in combination with is the proposition
is the proposition  . This asserts that it is possible, by incrementing
. This asserts that it is possible, by incrementing  sufficiently often, to make
sufficiently often, to make  equal to 7. This of course is not always true, e.g. if
equal to 7. This of course is not always true, e.g. if  is 8 to begin with, or 6.5, whence this proposition is not a theorem of dynamic logic. If
is 8 to begin with, or 6.5, whence this proposition is not a theorem of dynamic logic. If  is of type integer however, then this proposition is true if and only if
is of type integer however, then this proposition is true if and only if  is at most 7 to begin with, that is, it is just a roundabout way of saying
is at most 7 to begin with, that is, it is just a roundabout way of saying  .
.
Mathematical induction
can be obtained as the instance of A6 in which the proposition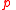 is instantiated as
is instantiated as 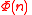 , the action
, the action  as
as 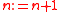 , and
, and  as
as  . The first two of these three instantiations are straightforward, converting A6 to
. The first two of these three instantiations are straightforward, converting A6 to  . However, the ostensibly simple substitution of
. However, the ostensibly simple substitution of  for
for  is not so simple as it brings out the so-called referential opacity of modal logic in the case when a modality can interfere with a substitution.
is not so simple as it brings out the so-called referential opacity of modal logic in the case when a modality can interfere with a substitution.
When we substituted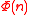 for
for 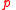 , we were thinking of the proposition symbol
, we were thinking of the proposition symbol 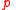 as a rigid designator
as a rigid designator
with respect to the modality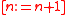 , meaning that it is the same proposition after incrementing
, meaning that it is the same proposition after incrementing  as before, even though incrementing
as before, even though incrementing  may impact its truth. Likewise, the action
may impact its truth. Likewise, the action  is still the same action after incrementing
is still the same action after incrementing  , even though incrementing
, even though incrementing  will result in its executing in a different environment. However,
will result in its executing in a different environment. However,  itself is not a rigid designator with respect to the modality
itself is not a rigid designator with respect to the modality 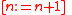 ; if it denotes 3 before incrementing
; if it denotes 3 before incrementing  , it denotes 4 after. So we can't just substitute
, it denotes 4 after. So we can't just substitute  for
for  everywhere in A6.
everywhere in A6.
One way of dealing with the opacity of modalities is to eliminate them. To this end, expand as the infinite conjunction
as the infinite conjunction 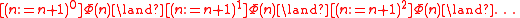 , that is, the conjunction over all
, that is, the conjunction over all  of
of 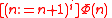 . Now apply A4 to turn
. Now apply A4 to turn 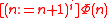 into
into  , having
, having  modalities. Then apply Hoare's axiom
modalities. Then apply Hoare's axiom  times to this to produce
times to this to produce  , then simplify this infinite conjunction to
, then simplify this infinite conjunction to  . This whole reduction should be applied to both instances of
. This whole reduction should be applied to both instances of  in A6, yielding
in A6, yielding 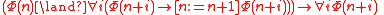 . The remaining modality can now be eliminated with one more use of Hoare's axiom to give
. The remaining modality can now be eliminated with one more use of Hoare's axiom to give  .
.
With the opaque modalities now out of the way, we can safely substitute for
for  in the usual manner of first-order logic
in the usual manner of first-order logic
to obtain Peano's celebrated axiom , namely mathematical induction.
, namely mathematical induction.
One subtlety we glossed over here is that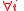 should be understood as ranging over the natural numbers, where
should be understood as ranging over the natural numbers, where  is the superscript in the expansion of
is the superscript in the expansion of  as the union of
as the union of 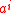 over all natural numbers
over all natural numbers  . The importance of keeping this typing information straight becomes apparent if
. The importance of keeping this typing information straight becomes apparent if  had been of type integer, or even real, for any of which A6 is perfectly valid as an axiom. As a case in point, if
had been of type integer, or even real, for any of which A6 is perfectly valid as an axiom. As a case in point, if  is a real variable and
is a real variable and 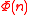 is the predicate
is the predicate  is a natural number, then axiom A6 after the first two substitutions, that is,
is a natural number, then axiom A6 after the first two substitutions, that is,  , is just as valid, that is, true in every state regardless of the value of
, is just as valid, that is, true in every state regardless of the value of  in that state, as when
in that state, as when  is of type natural number. If in a given state
is of type natural number. If in a given state  is a natural number, then the antecedent of the main implication of A6 holds, but then
is a natural number, then the antecedent of the main implication of A6 holds, but then  is also a natural number so the consequent also holds. If
is also a natural number so the consequent also holds. If  is not a natural number, then the antecedent is false and so A6 remains true regardless of the truth of the consequent. We could strengthen A6 to an equivalence
is not a natural number, then the antecedent is false and so A6 remains true regardless of the truth of the consequent. We could strengthen A6 to an equivalence  without impacting any of this, the other direction being provable from A5, from which we see that if the antecedent of A6 does happen to be false somewhere, then the consequent must be false.
without impacting any of this, the other direction being provable from A5, from which we see that if the antecedent of A6 does happen to be false somewhere, then the consequent must be false.
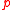 an action
an action 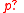 called a test. When
called a test. When 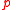 holds, the test
holds, the test 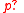 acts as a NOP, changing nothing while allowing the action to move on. When
acts as a NOP, changing nothing while allowing the action to move on. When 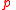 is false,
is false, 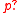 acts as BLOCK. Tests can be axiomatized as follows.
acts as BLOCK. Tests can be axiomatized as follows.
A8.
The corresponding theorem for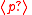 is:
is:
T8.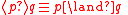
The construct if p then a else b is realized in dynamic logic as . This action expresses a guarded choice: if
. This action expresses a guarded choice: if 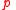 holds then
holds then 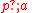 is equivalent to
is equivalent to  , whereas
, whereas 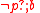 is equivalent to BLOCK, and
is equivalent to BLOCK, and 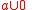 is equivalent to
is equivalent to  . Hence when
. Hence when  is true the performer of the action can only take the left branch, and when
is true the performer of the action can only take the left branch, and when 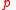 is false the right.
is false the right.
The construct while p do a is realized as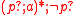 . This performs
. This performs  zero or more times and then performs
zero or more times and then performs 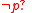 . As long as
. As long as 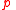 remains true, the
remains true, the 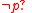 at the end blocks the performer from terminating the iteration prematurely, but as soon as it becomes false, further iterations of the body
at the end blocks the performer from terminating the iteration prematurely, but as soon as it becomes false, further iterations of the body 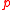 are blocked and the performer then has no choice but to exit via the test
are blocked and the performer then has no choice but to exit via the test  .
.
 denotes the nondeterministic action of setting
denotes the nondeterministic action of setting  to an arbitrary value.
to an arbitrary value. 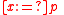 then says that
then says that 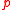 holds no matter what you set
holds no matter what you set  to, while
to, while 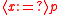 says that it is possible to set
says that it is possible to set  to a value that makes
to a value that makes 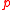 true.
true. 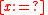 thus has the same meaning as the universal quantifier
thus has the same meaning as the universal quantifier 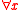 , while
, while 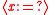 similarly corresponds to the existential quantifier
similarly corresponds to the existential quantifier  . That is, first-order logic can be understood as the dynamic logic of programs of the form
. That is, first-order logic can be understood as the dynamic logic of programs of the form  .
.
semantics or Kripke structures. This semantics carries over naturally to dynamic logic by interpreting worlds as states of a computer in the application to program verification, or states of our environment in applications to linguistics, AI, etc. One role for possible world semantics is to formalize the intuitive notions of truth and validity, which in turn permit the notions of soundness and completeness to be defined for axiom systems. An inference rule is sound when validity of its premises implies validity of its conclusion. An axiom system is sound when all its axioms are valid and its inference rules are sound. An axiom system is complete when every valid formula is derivable as a theorem of that system. These concepts apply to all systems of logic including dynamic logic.
has two types of terms, respectively assertions and data. As can be seen from the examples above, dynamic logic adds a third type of term denoting actions. The dynamic logic assertion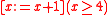 contains all three types:
contains all three types:  ,
,  , and
, and  are data,
are data, 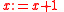 is an action, and
is an action, and  and
and 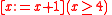 are assertions. Propositional logic is derived from first-order logic by omitting data terms and reasons only about abstract propositions, which may be simple propositional variable
are assertions. Propositional logic is derived from first-order logic by omitting data terms and reasons only about abstract propositions, which may be simple propositional variable
s or atoms or compound propositions built with such logical connectives as and, or, and not.
Propositional dynamic logic, or PDL, was derived from dynamic logic in 1977 by Michael J. Fischer
and Richard Ladner. PDL blends the ideas behind propositional logic and dynamic logic by adding actions while omitting data; hence the terms of PDL are actions and propositions. The TV example above is expressed in PDL whereas the next example involving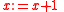 is in first-order DL. PDL is to (first-order) dynamic logic as propositional logic is to first-order logic.
is in first-order DL. PDL is to (first-order) dynamic logic as propositional logic is to first-order logic.
Fischer and Ladner showed in their 1977 paper that PDL satisfiability was of computational complexity at most nondeterministic exponential time, and at least deterministic exponential time in the worst case. This gap was closed in 1978 by Vaughan Pratt who showed that PDL was decidable in deterministic exponential time. In 1977, Krister Segerberg proposed a complete axiomatization of PDL, namely any complete axiomatization of modal logic K together with axioms A1-A6 as given above. Completeness proofs for Segerberg's axioms were found by Gabbay (unpublished note), Parikh (1978), Pratt (1979), and Kozen and Parikh (1981).
by expressing the Hoare formula as
as  . The approach was later published in 1976 as a logical system in its own right. The system parallels A. Salwicki's system of Algorithmic Logic and Edsger Dijkstra
. The approach was later published in 1976 as a logical system in its own right. The system parallels A. Salwicki's system of Algorithmic Logic and Edsger Dijkstra
's notion of weakest-precondition predicate transformer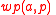 , with
, with 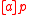 corresponding to Dijkstra's
corresponding to Dijkstra's 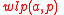 , weakest liberal precondition. Those logics however made no connection with either modal logic, Kripke semantics, regular expressions, or the calculus of binary relations; dynamic logic therefore can be viewed as a refinement of algorithmic logic and Predicate Transformers
, weakest liberal precondition. Those logics however made no connection with either modal logic, Kripke semantics, regular expressions, or the calculus of binary relations; dynamic logic therefore can be viewed as a refinement of algorithmic logic and Predicate Transformers
that connects them up to the axiomatics and Kripke semantics of modal logic as well as to the calculi of binary relations and regular expressions.
, another variant of modal logic sharing many common features with dynamic logic, differs from all of the above-mentioned logics by being what Pnueli has characterized as an "endogenous" logic, the others being "exogenous" logics. By this Pnueli meant that temporal logic assertions are interpreted within a universal behavioral framework in which a single global situation changes with the passage of time, whereas the assertions of the other logics are made externally to the multiple actions about which they speak. The advantage of the endogenous approach is that it makes no fundamental assumptions about what causes what as the environment changes with time. Instead a temporal logic formula can talk about two unrelated parts of a system, which because they are unrelated tacitly evolve in parallel. In effect ordinary logical conjunction of temporal assertions is the concurrent composition operator of temporal logic. The simplicity of this approach to concurrency has resulted in temporal logic being the modal logic of choice for reasoning about concurrent systems with its aspects of synchronization, interference, independence, deadlock, livelock, fairness, etc.
These concerns of concurrency would appear to be less central to linguistics, philosophy, and artificial intelligence, the areas in which dynamic logic is most often encountered nowadays.
For a comprehensive treatment of dynamic logic see the book by David Harel
et al. cited below.
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.
Language
Modal logicModal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
is characterized by the modal operator
Modal operator
In modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...
s
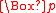 (box p) asserting that
(box p) asserting that  is necessarily the case, and
is necessarily the case, and  (diamond p) asserting that
(diamond p) asserting that 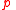 is possibly the case. Dynamic logic extends this by associating to every action
is possibly the case. Dynamic logic extends this by associating to every action  the modal operators
the modal operators  and
and  , thereby making it a multimodal logic
, thereby making it a multimodal logicMultimodal logic
A multimodal logic is a modal logic that has more than one primitive modal operator. They find substantial applications in theoretical computer science....
. The meaning of
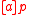 is that after performing action
is that after performing action  it is necessarily the case that
it is necessarily the case that  holds, that is,
holds, that is,  must bring about
must bring about 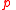 . The meaning of
. The meaning of 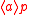 is that after performing
is that after performing  it is possible that
it is possible that 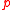 holds, that is,
holds, that is,  might bring about
might bring about 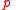 . These operators are related by
. These operators are related by  and
and  , analogously to the relationship between the universal (
, analogously to the relationship between the universal ( ) and existential (
) and existential ( ) quantifiers.
) quantifiers.Dynamic logic permits compound actions built up from smaller actions. While the basic control operators of any programming language could be used for this purpose, Kleene's regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
operators are a good match to modal logic. Given actions
 and
and  , the compound action
, the compound action  , choice, also written
, choice, also written  or
or 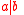 , is performed by performing one of
, is performed by performing one of  or
or  . The compound action
. The compound action  , sequence, is performed by performing first
, sequence, is performed by performing first  and then
and then  . The compound action
. The compound action  , iteration, is performed by performing
, iteration, is performed by performing  zero or more times, sequentially. The constant action
zero or more times, sequentially. The constant action  or BLOCK does nothing and does not terminate, whereas the constant action
or BLOCK does nothing and does not terminate, whereas the constant action 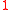 or SKIP or NOP, definable as
or SKIP or NOP, definable as  , does nothing but does terminate.
, does nothing but does terminate.Axioms
These operators can be axiomatized in dynamic logic as follows, taking as already given a suitable axiomatization of modal logicModal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
including such axioms for modal operators as the above-mentioned axiom
 and the two inference rules modus ponens (
and the two inference rules modus ponens (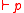 and
and 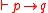 implies
implies 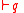 ) and necessitation (
) and necessitation (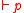 implies
implies  ).
).A1.
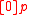
A2.
A3.
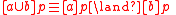
A4.

A5.
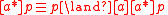
A6.

Axiom A1 makes the empty promise that when BLOCK terminates,
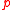 will hold, even if
will hold, even if  is the proposition false. (Thus BLOCK abstracts the essence of the action of hell freezing over.)
is the proposition false. (Thus BLOCK abstracts the essence of the action of hell freezing over.)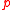 into itself.
into itself. or
or  must bring about
must bring about 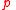 , then
, then  must bring about
must bring about 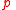 and likewise for
and likewise for  , and conversely.
, and conversely. and then
and then  must bring about
must bring about 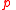 , then
, then  must bring about a situation in which
must bring about a situation in which  must bring about
must bring about  .
. of Kleene algebra
of Kleene algebraKleene algebra
In mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
.
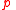 holds now, and no matter how often we perform
holds now, and no matter how often we perform  it remains the case that the truth of
it remains the case that the truth of 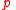 after that performance entails its truth after one more performance of
after that performance entails its truth after one more performance of  , then
, then 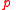 must remain true no matter how often we perform
must remain true no matter how often we perform  . A6 is recognizable as mathematical induction
. A6 is recognizable as mathematical inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
with the action n := n+1 of incrementing n generalized to arbitrary actions
 .
.Derivations
The modal logic axiom permits the derivation of the following six theorems corresponding to the above:
permits the derivation of the following six theorems corresponding to the above:T1.

T2.
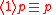
T3.
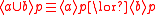
T4.

T5.

T6.

T1 asserts the impossibility of bringing anything about by performing BLOCK.
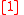 and
and 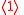 have the same force.
have the same force. or
or  could bring about
could bring about  , then either
, then either  or
or  alone could bring about
alone could bring about  .
.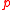 by performing
by performing  sufficiently often, then either
sufficiently often, then either 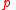 is true now or it is possible to perform
is true now or it is possible to perform  repeatedly to bring about a situation where
repeatedly to bring about a situation where 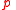 is (still) false but one more performance of
is (still) false but one more performance of  could bring about
could bring about 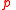 .
.Box and diamond are entirely symmetric with regard to which one takes as primitive. An alternative axiomatization would have been to take the theorems T1-T6 as axioms, from which we could then have derived A1-A6 as theorems.
The difference between implication and inference is the same in dynamic logic as in any other logic: whereas the implication
 asserts that if
asserts that if 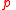 is true then so is
is true then so is  , the inference
, the inference  asserts that if
asserts that if 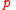 is valid then so is
is valid then so is  . However the dynamic nature of dynamic logic moves this distinction out of the realm of abstract axiomatics into the common-sense experience of situations in flux. The inference rule
. However the dynamic nature of dynamic logic moves this distinction out of the realm of abstract axiomatics into the common-sense experience of situations in flux. The inference rule  , for example, is sound because its premise asserts that
, for example, is sound because its premise asserts that 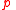 holds at all times, whence no matter where
holds at all times, whence no matter where  might take us,
might take us, 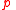 will be true there. The implication
will be true there. The implication 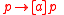 is not valid, however, because the truth of
is not valid, however, because the truth of 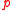 at the present moment is no guarantee of its truth after performing
at the present moment is no guarantee of its truth after performing  . For example,
. For example, 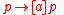 will be true in any situation where
will be true in any situation where 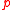 is false, or in any situation where
is false, or in any situation where 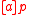 is true, but the assertion
is true, but the assertion 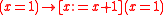 is false in any situation where
is false in any situation where  has value 1, and therefore is not valid.
has value 1, and therefore is not valid.Derived rules of inference
As for modal logic, the inference rules modus ponens and necessitation suffice also for dynamic logic as the only primitive rules it needs, as noted above. However, as usual in logic, many more rules can be derived from these with the help of the axioms. An example instance of such a derived rule in dynamic logic is that if kicking a broken TV once can't possibly fix it, then repeatedly kicking it can't possibly fix it either. Writing for the action of kicking the TV, and
for the action of kicking the TV, and  for the proposition that the TV is broken, dynamic logic expresses this inference as
for the proposition that the TV is broken, dynamic logic expresses this inference as 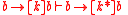 , having as premise
, having as premise 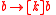 and as conclusion
and as conclusion 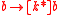 . The meaning of
. The meaning of  is that it is guaranteed that after kicking the TV, it is broken. Hence the premise
is that it is guaranteed that after kicking the TV, it is broken. Hence the premise 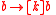 means that if the TV is broken, then after kicking it once it will still be broken.
means that if the TV is broken, then after kicking it once it will still be broken.  denotes the action of kicking the TV zero or more times. Hence the conclusion
denotes the action of kicking the TV zero or more times. Hence the conclusion  means that if the TV is broken, then after kicking it zero or more times it will still be broken. For if not, then after the second-to-last kick the TV would be in a state where kicking it once more would fix it, which the premise claims can never happen under any circumstances.
means that if the TV is broken, then after kicking it zero or more times it will still be broken. For if not, then after the second-to-last kick the TV would be in a state where kicking it once more would fix it, which the premise claims can never happen under any circumstances.The inference
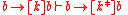 is sound. However the implication
is sound. However the implication  is not valid because we can easily find situations in which
is not valid because we can easily find situations in which 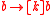 holds but
holds but 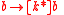 does not. In any such counterexample situation,
does not. In any such counterexample situation,  must hold but
must hold but  must be false, while
must be false, while 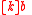 however must be true. But this could happen in any situation where the TV is broken but can be revived with two kicks. The implication fails (is not valid) because it only requires that
however must be true. But this could happen in any situation where the TV is broken but can be revived with two kicks. The implication fails (is not valid) because it only requires that 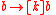 hold now, whereas the inference succeeds (is sound) because it requires that
hold now, whereas the inference succeeds (is sound) because it requires that 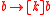 hold in all situations, not just the present one.
hold in all situations, not just the present one.An example of a valid implication is the proposition
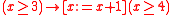 . This says that if
. This says that if  is greater or equal to 3, then after incrementing
is greater or equal to 3, then after incrementing  ,
,  must be greater or equal to 4. In the case of deterministic actions
must be greater or equal to 4. In the case of deterministic actions  that are guaranteed to terminate, such as
that are guaranteed to terminate, such as 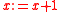 , must and might have the same force, that is,
, must and might have the same force, that is,  and
and  have the same meaning. Hence the above proposition is equivalent to
have the same meaning. Hence the above proposition is equivalent to 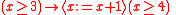 asserting that if
asserting that if  is greater or equal to 3 then after performing
is greater or equal to 3 then after performing  ,
,  might be greater or equal to 4.
might be greater or equal to 4.Assignment
The general form of an assignment statement is where
where  is a variable and
is a variable and  is an expression built from constants and variables with whatever operations are provided by the language, such as addition and multiplication. The Hoare axiom for assignment is not given as a single axiom but rather as an axiom schema.
is an expression built from constants and variables with whatever operations are provided by the language, such as addition and multiplication. The Hoare axiom for assignment is not given as a single axiom but rather as an axiom schema.A7.
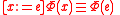
This is a schema in the sense that
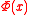 can be instantiated with any formula
can be instantiated with any formula  containing zero or more instances of a variable
containing zero or more instances of a variable  . The meaning of
. The meaning of 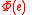 is
is  with those occurrences of
with those occurrences of  that occur free in
that occur free in  , i.e. not bound by some quantifier as in
, i.e. not bound by some quantifier as in 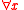 , replaced by
, replaced by  . For example we may instantiate A7 with
. For example we may instantiate A7 with 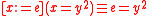 , or with
, or with  . Such an axiom schema allows infinitely many axioms having a common form to be written as a finite expression connoting that form.
. Such an axiom schema allows infinitely many axioms having a common form to be written as a finite expression connoting that form.The instance
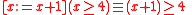 of A7 allows us to calculate mechanically that the example
of A7 allows us to calculate mechanically that the example 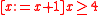 encountered a few paragraphs ago is equivalent to
encountered a few paragraphs ago is equivalent to 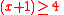 , which in turn is equivalent to
, which in turn is equivalent to  by elementary algebra
by elementary algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
.
An example illustrating assignment in combination with
 is the proposition
is the proposition  . This asserts that it is possible, by incrementing
. This asserts that it is possible, by incrementing  sufficiently often, to make
sufficiently often, to make  equal to 7. This of course is not always true, e.g. if
equal to 7. This of course is not always true, e.g. if  is 8 to begin with, or 6.5, whence this proposition is not a theorem of dynamic logic. If
is 8 to begin with, or 6.5, whence this proposition is not a theorem of dynamic logic. If  is of type integer however, then this proposition is true if and only if
is of type integer however, then this proposition is true if and only if  is at most 7 to begin with, that is, it is just a roundabout way of saying
is at most 7 to begin with, that is, it is just a roundabout way of saying  .
.Mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
can be obtained as the instance of A6 in which the proposition
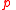 is instantiated as
is instantiated as 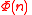 , the action
, the action  as
as 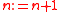 , and
, and  as
as  . The first two of these three instantiations are straightforward, converting A6 to
. The first two of these three instantiations are straightforward, converting A6 to  . However, the ostensibly simple substitution of
. However, the ostensibly simple substitution of  for
for  is not so simple as it brings out the so-called referential opacity of modal logic in the case when a modality can interfere with a substitution.
is not so simple as it brings out the so-called referential opacity of modal logic in the case when a modality can interfere with a substitution.When we substituted
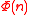 for
for 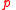 , we were thinking of the proposition symbol
, we were thinking of the proposition symbol 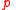 as a rigid designator
as a rigid designatorRigid designator
In modal logic and the philosophy of language, a term is said to be a rigid designator when it designates the same thing in all possible worlds in which that thing exists and does not designate anything else in those possible worlds in which that thing does not exist...
with respect to the modality
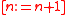 , meaning that it is the same proposition after incrementing
, meaning that it is the same proposition after incrementing  as before, even though incrementing
as before, even though incrementing  may impact its truth. Likewise, the action
may impact its truth. Likewise, the action  is still the same action after incrementing
is still the same action after incrementing  , even though incrementing
, even though incrementing  will result in its executing in a different environment. However,
will result in its executing in a different environment. However,  itself is not a rigid designator with respect to the modality
itself is not a rigid designator with respect to the modality 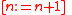 ; if it denotes 3 before incrementing
; if it denotes 3 before incrementing  , it denotes 4 after. So we can't just substitute
, it denotes 4 after. So we can't just substitute  for
for  everywhere in A6.
everywhere in A6.One way of dealing with the opacity of modalities is to eliminate them. To this end, expand
 as the infinite conjunction
as the infinite conjunction 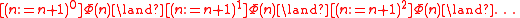 , that is, the conjunction over all
, that is, the conjunction over all  of
of 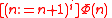 . Now apply A4 to turn
. Now apply A4 to turn 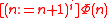 into
into  , having
, having  modalities. Then apply Hoare's axiom
modalities. Then apply Hoare's axiom  times to this to produce
times to this to produce  , then simplify this infinite conjunction to
, then simplify this infinite conjunction to  . This whole reduction should be applied to both instances of
. This whole reduction should be applied to both instances of  in A6, yielding
in A6, yielding 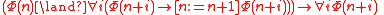 . The remaining modality can now be eliminated with one more use of Hoare's axiom to give
. The remaining modality can now be eliminated with one more use of Hoare's axiom to give  .
.With the opaque modalities now out of the way, we can safely substitute
 for
for  in the usual manner of first-order logic
in the usual manner of first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
to obtain Peano's celebrated axiom
 , namely mathematical induction.
, namely mathematical induction.One subtlety we glossed over here is that
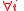 should be understood as ranging over the natural numbers, where
should be understood as ranging over the natural numbers, where  is the superscript in the expansion of
is the superscript in the expansion of  as the union of
as the union of 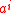 over all natural numbers
over all natural numbers  . The importance of keeping this typing information straight becomes apparent if
. The importance of keeping this typing information straight becomes apparent if  had been of type integer, or even real, for any of which A6 is perfectly valid as an axiom. As a case in point, if
had been of type integer, or even real, for any of which A6 is perfectly valid as an axiom. As a case in point, if  is a real variable and
is a real variable and 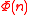 is the predicate
is the predicate  is a natural number, then axiom A6 after the first two substitutions, that is,
is a natural number, then axiom A6 after the first two substitutions, that is,  , is just as valid, that is, true in every state regardless of the value of
, is just as valid, that is, true in every state regardless of the value of  in that state, as when
in that state, as when  is of type natural number. If in a given state
is of type natural number. If in a given state  is a natural number, then the antecedent of the main implication of A6 holds, but then
is a natural number, then the antecedent of the main implication of A6 holds, but then  is also a natural number so the consequent also holds. If
is also a natural number so the consequent also holds. If  is not a natural number, then the antecedent is false and so A6 remains true regardless of the truth of the consequent. We could strengthen A6 to an equivalence
is not a natural number, then the antecedent is false and so A6 remains true regardless of the truth of the consequent. We could strengthen A6 to an equivalence  without impacting any of this, the other direction being provable from A5, from which we see that if the antecedent of A6 does happen to be false somewhere, then the consequent must be false.
without impacting any of this, the other direction being provable from A5, from which we see that if the antecedent of A6 does happen to be false somewhere, then the consequent must be false.Test
Dynamic logic associates to every proposition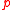 an action
an action 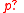 called a test. When
called a test. When 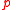 holds, the test
holds, the test 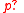 acts as a NOP, changing nothing while allowing the action to move on. When
acts as a NOP, changing nothing while allowing the action to move on. When 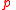 is false,
is false, 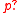 acts as BLOCK. Tests can be axiomatized as follows.
acts as BLOCK. Tests can be axiomatized as follows.A8.

The corresponding theorem for
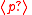 is:
is:T8.
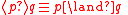
The construct if p then a else b is realized in dynamic logic as
 . This action expresses a guarded choice: if
. This action expresses a guarded choice: if 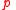 holds then
holds then 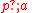 is equivalent to
is equivalent to  , whereas
, whereas 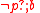 is equivalent to BLOCK, and
is equivalent to BLOCK, and 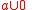 is equivalent to
is equivalent to  . Hence when
. Hence when  is true the performer of the action can only take the left branch, and when
is true the performer of the action can only take the left branch, and when 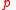 is false the right.
is false the right.The construct while p do a is realized as
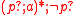 . This performs
. This performs  zero or more times and then performs
zero or more times and then performs 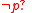 . As long as
. As long as 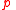 remains true, the
remains true, the 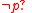 at the end blocks the performer from terminating the iteration prematurely, but as soon as it becomes false, further iterations of the body
at the end blocks the performer from terminating the iteration prematurely, but as soon as it becomes false, further iterations of the body 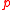 are blocked and the performer then has no choice but to exit via the test
are blocked and the performer then has no choice but to exit via the test  .
.Quantification as random assignment
The random-assignment statement denotes the nondeterministic action of setting
denotes the nondeterministic action of setting  to an arbitrary value.
to an arbitrary value. 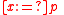 then says that
then says that 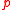 holds no matter what you set
holds no matter what you set  to, while
to, while 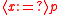 says that it is possible to set
says that it is possible to set  to a value that makes
to a value that makes 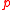 true.
true. 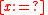 thus has the same meaning as the universal quantifier
thus has the same meaning as the universal quantifier 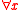 , while
, while 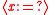 similarly corresponds to the existential quantifier
similarly corresponds to the existential quantifier  . That is, first-order logic can be understood as the dynamic logic of programs of the form
. That is, first-order logic can be understood as the dynamic logic of programs of the form  .
.Possible-world semantics
Modal logic is most commonly interpreted in terms of possible worldPossible world
In philosophy and logic, the concept of a possible world is used to express modal claims. The concept of possible worlds is common in contemporary philosophical discourse and has also been disputed.- Possibility, necessity, and contingency :...
semantics or Kripke structures. This semantics carries over naturally to dynamic logic by interpreting worlds as states of a computer in the application to program verification, or states of our environment in applications to linguistics, AI, etc. One role for possible world semantics is to formalize the intuitive notions of truth and validity, which in turn permit the notions of soundness and completeness to be defined for axiom systems. An inference rule is sound when validity of its premises implies validity of its conclusion. An axiom system is sound when all its axioms are valid and its inference rules are sound. An axiom system is complete when every valid formula is derivable as a theorem of that system. These concepts apply to all systems of logic including dynamic logic.
Propositional dynamic logic (PDL)
Ordinary or first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
has two types of terms, respectively assertions and data. As can be seen from the examples above, dynamic logic adds a third type of term denoting actions. The dynamic logic assertion
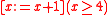 contains all three types:
contains all three types:  ,
,  , and
, and  are data,
are data, 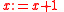 is an action, and
is an action, and  and
and 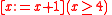 are assertions. Propositional logic is derived from first-order logic by omitting data terms and reasons only about abstract propositions, which may be simple propositional variable
are assertions. Propositional logic is derived from first-order logic by omitting data terms and reasons only about abstract propositions, which may be simple propositional variablePropositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s or atoms or compound propositions built with such logical connectives as and, or, and not.
Propositional dynamic logic, or PDL, was derived from dynamic logic in 1977 by Michael J. Fischer
Michael J. Fischer
Michael John Fischer is a computer scientist who works in the fields of distributed computing, parallel computing, cryptography, algorithms and data structures, and computational complexity.-Career:...
and Richard Ladner. PDL blends the ideas behind propositional logic and dynamic logic by adding actions while omitting data; hence the terms of PDL are actions and propositions. The TV example above is expressed in PDL whereas the next example involving
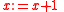 is in first-order DL. PDL is to (first-order) dynamic logic as propositional logic is to first-order logic.
is in first-order DL. PDL is to (first-order) dynamic logic as propositional logic is to first-order logic.Fischer and Ladner showed in their 1977 paper that PDL satisfiability was of computational complexity at most nondeterministic exponential time, and at least deterministic exponential time in the worst case. This gap was closed in 1978 by Vaughan Pratt who showed that PDL was decidable in deterministic exponential time. In 1977, Krister Segerberg proposed a complete axiomatization of PDL, namely any complete axiomatization of modal logic K together with axioms A1-A6 as given above. Completeness proofs for Segerberg's axioms were found by Gabbay (unpublished note), Parikh (1978), Pratt (1979), and Kozen and Parikh (1981).
History
Dynamic logic was developed by Vaughan Pratt in 1974 in notes for a class on program verification as an approach to assigning meaning to Hoare logicHoare logic
Hoare logic is a formal system with a set of logical rules for reasoning rigorously about the correctness of computer programs. It was proposed in 1969 by the British computer scientist and logician C. A. R. Hoare, and subsequently refined by Hoare and other researchers...
by expressing the Hoare formula
 as
as  . The approach was later published in 1976 as a logical system in its own right. The system parallels A. Salwicki's system of Algorithmic Logic and Edsger Dijkstra
. The approach was later published in 1976 as a logical system in its own right. The system parallels A. Salwicki's system of Algorithmic Logic and Edsger DijkstraEdsger Dijkstra
Edsger Wybe Dijkstra ; ) was a Dutch computer scientist. He received the 1972 Turing Award for fundamental contributions to developing programming languages, and was the Schlumberger Centennial Chair of Computer Sciences at The University of Texas at Austin from 1984 until 2000.Shortly before his...
's notion of weakest-precondition predicate transformer
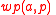 , with
, with 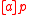 corresponding to Dijkstra's
corresponding to Dijkstra's 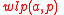 , weakest liberal precondition. Those logics however made no connection with either modal logic, Kripke semantics, regular expressions, or the calculus of binary relations; dynamic logic therefore can be viewed as a refinement of algorithmic logic and Predicate Transformers
, weakest liberal precondition. Those logics however made no connection with either modal logic, Kripke semantics, regular expressions, or the calculus of binary relations; dynamic logic therefore can be viewed as a refinement of algorithmic logic and Predicate TransformersPredicate transformer semantics
Predicate transformer semantics was introduced by Dijkstra in his seminal paper "Guarded commands, nondeterminacy and formal derivation of programs". They define the semantics of an imperative programming paradigm by assigning to each statement in this language a corresponding predicate...
that connects them up to the axiomatics and Kripke semantics of modal logic as well as to the calculi of binary relations and regular expressions.
The Concurrency Challenge
Hoare logic, algorithmic logic, weakest preconditions, and dynamic logic are all well suited to discourse and reasoning about sequential behavior. Extending these logics to concurrent behavior however has proved problematic. There are various approaches but all of them lack the elegance of the sequential case. In contrast Amir Pnueli's 1977 system of temporal logicTemporal logic
In logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
, another variant of modal logic sharing many common features with dynamic logic, differs from all of the above-mentioned logics by being what Pnueli has characterized as an "endogenous" logic, the others being "exogenous" logics. By this Pnueli meant that temporal logic assertions are interpreted within a universal behavioral framework in which a single global situation changes with the passage of time, whereas the assertions of the other logics are made externally to the multiple actions about which they speak. The advantage of the endogenous approach is that it makes no fundamental assumptions about what causes what as the environment changes with time. Instead a temporal logic formula can talk about two unrelated parts of a system, which because they are unrelated tacitly evolve in parallel. In effect ordinary logical conjunction of temporal assertions is the concurrent composition operator of temporal logic. The simplicity of this approach to concurrency has resulted in temporal logic being the modal logic of choice for reasoning about concurrent systems with its aspects of synchronization, interference, independence, deadlock, livelock, fairness, etc.
These concerns of concurrency would appear to be less central to linguistics, philosophy, and artificial intelligence, the areas in which dynamic logic is most often encountered nowadays.
For a comprehensive treatment of dynamic logic see the book by David Harel
David Harel
David Harel is a professor of computer science at the Weizmann Institute of Science in Israel. Born in London, England, he was Dean of the Faculty of Mathematics and Computer Science at the institute for seven years.-Biography:...
et al. cited below.
External links
- Semantical Considerations on Floyd-Hoare Logic (original paper on dynamic logic)

