Maximum spacing estimation - AbsoluteAstronomy.com

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model

Parametric model

In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...

. The method requires maximization of the geometric mean of spacings in the data, which are the differences between the values of the cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

at neighbouring data points.

The concept underlying the method is based on the probability integral transform

Probability integral transform

In statistics, the probability integral transform or transformation relates to the result that data values that are modelled as being random variables from any given continuous distribution can be converted to random variables having a uniform distribution...

, in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity.

One of the most common methods for estimating the parameters of a distribution from data, the method of maximum likelihood

Maximum likelihood

In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....

(MLE), can break down in various cases, such as involving certain mixtures of continuous distributions. In these cases the method of maximum spacing estimation may be successful.

Apart from its use in pure mathematics and statistics, the trial applications of the method have been reported using data from fields such as hydrology

Hydrology

Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...

, econometrics

Econometrics

Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...

, and others.

History and usage

The MSE method was derived independently by Russel Cheng and Nik Amin at the University of Wales Institute of Science and Technology

Cardiff University

Cardiff University is a leading research university located in the Cathays Park area of Cardiff, Wales, United Kingdom. It received its Royal charter in 1883 and is a member of the Russell Group of Universities. The university is consistently recognised as providing high quality research-based...

, and Bo Ranneby at the Swedish University of Agricultural Sciences

Swedish University of Agricultural Sciences

The Swedish University of Agricultural Sciences or Sveriges Lantbruksuniversitet is a university in Sweden. Although its head office is located in Ultuna, Uppsala, the university has several campuses in different parts of Sweden, the other main facilities being Alnarp in Lomma Municipality, Skara,...

. The authors explained that due to the probability integral transform

Probability integral transform

at the true parameter, the “spacing” between each observation should be uniformly distributed. This would imply that the difference between the values of the cumulative distribution function

Cumulative distribution function

at consecutive observations should be equal. This is the case that maximizes the geometric mean

Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...

of such spacings, so solving for the parameters that maximize the geometric mean would achieve the “best” fit as defined this way. justified the method by demonstrating that it is an estimator of the Kullback–Leibler divergence

Kullback–Leibler divergence

In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...

, similar to maximum likelihood estimation, but with more robust properties for various classes of problems.

There are certain distributions, especially those with three or more parameters, whose likelihoods may become infinite along certain paths in the parameter space

Parameter space

In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....

. Using maximum likelihood to estimate these parameters often breaks down, with one parameter tending to the specific value that causes the likelihood to be infinite, rendering the other parameters inconsistent. The method of maximum spacings, however, being dependent on the difference between points on the cumulative distribution function and not individual likelihood points, does not have this issue, and will return valid results over a much wider array of distributions.

The distributions that tend to have likelihood issues are often those used to model physical phenomena. seek to analyze flood alleviation methods, which requires accurate models of river flood effects. The distributions that better model these effects are all three-parameter models, which suffer from the infinite likelihood issue described above, leading to Hall’s investigation of the maximum spacing procedure. , when comparing the method to maximum likelihood, use various data sets ranging from a set on the oldest ages at death in Sweden between 1905 and 1958 to a set containing annual maximum wind speeds.

Definition

Given an iid random sample

Random sample

In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...

{x₁, …, x_n} of size n from a univariate distribution

Univariate distribution

In statistics, a univariate distribution is a probability distribution of only one random variable. This is in contrast to a multivariate distribution, the probability distribution of a random vector.-Further reading:...

with cdf F(x;θ₀), where θ₀ ∈ Θ is an unknown parameter to be estimated

Estimation

Estimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...

, let {x₍₁₎, …, x_(n)} be the corresponding ordered

Order statistic

In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....

sample, that is the result of sorting of all observations from smallest to largest. For convenience also denote x₍₀₎ = −∞ and x_(n+1) = +∞.

Define the spacings as the “gaps” between the values of the distribution function at adjacent ordered points: The actual definition is sourced to , but without direct access to that paper, sourcing is given to which defines the spacings in passing. — Editor.
Pyke (1965) starts with “review of previous results known about spacings”, which implies that he hasn't invented them. In fact the first work about the spacings he mentions is “Whitworth (1887)”, although no actual reference was given.

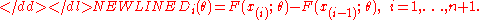
Then the maximum spacing estimator of θ₀ is defined as a value that maximizes the logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

of the geometric mean

Geometric mean

of sample spacings:

By the inequality of arithmetic and geometric means

Inequality of arithmetic and geometric means

In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...

, function S_n(θ) is bounded from above by −ln(n+1), and thus the maximum has to exist at least in the supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

sense.

Note that some authors define the function S_n(θ) somewhat differently. In particular, multiplies each D_i by a factor of (n+1), whereas omit the factor in front of the sum and add the “−” sign in order to turn the maximization into minimization. As these are constants with respect to θ, the modifications do not alter the location of the maximum of the function S_n.

Example 1

Suppose two values x₍₁₎ = 2, x₍₂₎ = 4 were sampled from the exponential distribution

Exponential distribution

In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

F(x;λ) = 1 − e^−xλ, x ≥ 0 with unknown parameter λ > 0. In order to construct the MSE we have to first find the spacings:

i	F(x_(i))	F(x_(i−1))	D_i = F(x_(i)) − F(x_(i−1))
1	1 − e^−2λ	0	1 − e^−2λ
2	1 − e^−4λ	1 − e^−2λ	e^−2λ − e^−4λ
3	1	1 − e^−4λ	e^−4λ

The process continues by finding the λ that maximizes the geometric mean of the “difference” column. Using the convention that ignores taking the (n+1)^st root, this turns into the maximization of the following product: (1 − e^−2λ) · (e^−2λ − e^−4λ) · (e^−4λ). Letting μ = e^−2λ, the problem becomes finding the maximum of μ⁵−2μ⁴+μ³. Differentiating, the μ has to satisfy 5μ⁴−8μ³+3μ² = 0. This equation has roots 0, 0.6, and 1. As μ is actually e^−2λ, it has to be greater than zero but less than one. Therefore, the only acceptable solution is

which corresponds to an exponential distribution with a mean of ≈ 3.915. For comparison, the maximum likelihood estimate of λ is the inverse of the sample mean, 3, so λ_MLE = ⅓ ≈ 0.333.

Example 2

Suppose {x₍₁₎, …, x_(n)} is the ordered sample from a uniform distribution

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

U(a,b) with unknown endpoints a and b. The cumulative distribution function is F(x;a,b) = (x−a)÷(b−a) when x∈[a,b]. Therefore individual spacings are given by

Calculating the geometric mean and then taking the logarithm, statistic S_n will be equal to

Here only the first three terms depend on the parameters a and b. Differentiating with respect to those parameters and solving the resulting linear system, the maximum spacing estimates will be

\hat{a} = \frac{nx_{(1)} - x_{(n)}}{n-1},\ \ \hat{b} = \frac{nx_{(n)}-x_{(1)}}{n-1}.
These are known to be the uniformly minimum variance unbiased (UMVU) estimators for the continuous uniform distribution. In comparison, the maximum likelihood estimates for this problem

\scriptstyle\hat{a}=x_{(1)}

and

\scriptstyle\hat{b}=x_{(n)}

are biased and have higher mean-squared error.

Consistency and efficiency

The maximum spacing estimator is a consistent estimator

Consistent estimator

In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

in that it converges in probability to the true value of the parameter, θ₀, as the sample size increases to infinity. The consistency of maximum spacing estimation holds under much more general conditions than for maximum likelihood

Maximum likelihood

estimators. In particular, in cases where the underlying distribution is J-shaped, maximum likelihood will fail where MSE succeeds. An example of a J-shaped density is the Weibull distribution, specifically a shifted Weibull, with a shape parameter

Shape parameter

In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...

less than 1. The density will tend to infinity as x approaches the location parameter

Location parameter

In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...

rendering estimates of the other parameters inconsistent.

Maximum spacing estimators are also at least as asymptotically efficient as maximum likelihood estimators, where the latter exist. However, MSEs may exist in cases where MLEs do not.

Sensitivity

Maximum spacing estimators are sensitive to closely spaced observations, and especially ties. Given

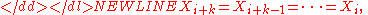
we get

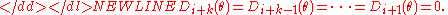
When the ties are due to multiple observations, the repeated spacings (those that would otherwise be zero) should be replaced by the corresponding likelihood. That is, one should substitute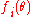

for

, as

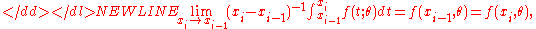
since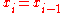

.

When ties are due to rounding error, suggest another method to remove the effects.
There appear to be some minor typographical errors in the paper. For example, in section 4.2, equation (4.1), the rounding replacement for

, should not have the log term. In section 1, equation (1.2),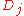

is defined to be the spacing itself, and

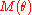is the negative sum of the logs of

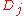. If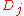

is logged at this step, the result is always =<0, as the difference between two adjacent points on a cumulative distribution is always ≤ 1, and strictly <1 unless there are only two points at the bookends. Also, in section 4.3, on page 392, calculation shows that it is the variance

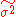which has MPS estimate of 6.87, not the standard deviation

. -- Editor
Given r tied observations from x_i to x_i+r−1, let δ represent the round-off error

Round-off error

A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...

. All of the true values should then fall in the range

. The corresponding points on the distribution should now fall between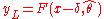

and

. Cheng and Stephens suggest assuming that the rounded values are uniformly spaced

Uniform distribution (continuous)

in this interval, by defining

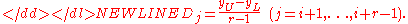
The MSE method is also sensitive to secondary clustering. One example of this phenomenon is when a set of observations is thought to come from a single normal distribution, but in fact comes from a mixture

Mixture (probability)

In probability theory and statistics, a mixture is a combination of two or more probability distributions. The concept arises in two contexts:* A mixture defining a new probability distribution from some existing ones, as in a mixture density...

normals with different means. A second example is when the data is thought to come from an exponential distribution

Exponential distribution

In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

, but actually comes from a gamma distribution. In the latter case, smaller spacings may occur in the lower tail. A high value of M(θ) would indicate this secondary clustering effect, and suggesting a closer look at the data is required.

Goodness of fit

The statistic S_n(θ) is also a form of Moran or Moran-Darling statistic, M(θ), which can be used to test goodness of fit

Goodness of fit

The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...

.
The literature refers to related statistics as Moran or Moran-Darling statistics. For example, analyze the form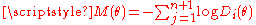

where

is defined as above. use the same form as well. However, uses the form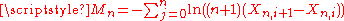

, with the additional factor of

inside the logged summation. The extra factors will make a difference in terms of the expected mean and variance of the statistic. For consistency, this article will continue to use the Cheng & Amin/Wong & Li form. -- Editor
It has been shown that the statistic, when defined as

is asymptotically normal, and that a chi-squared approximation exists for small samples. In the case where we know the true parameter

, show that the statistic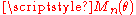

has a normal distribution with

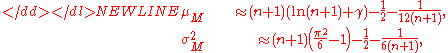
where γ is the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

which is approximately 0.57722. leave out the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

from their description. -- Editor

The distribution can also be approximated by that of

, where

,
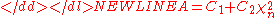in which

and where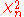

follows a chi-squared distribution with

degrees of freedom

Degrees of freedom (statistics)

In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...

. Therefore, to test the hypothesis

that a random sample of

values comes from the distribution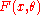

, the statistic

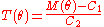can be calculated. Then

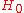should be rejected with significance

Statistical significance

In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....

if the value is greater than the critical value

Critical value

-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...

of the appropriate chi-squared distribution.

Where θ₀ is being estimated by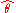

, showed that

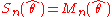has the same asymptotic mean and variance as in the known case. However, the test statistic to be used requires the addition of a bias correction term and is:

where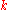

is the number of parameters in the estimate.

Alternate measures and spacings

generalized the MSE method to approximate other measures

F-divergence

In probability theory, an ƒ-divergence is a function Df that measures the difference between two probability distributions P and Q...

besides the Kullback–Leibler measure. further expanded the method to investigate properties of estimators using higher order spacings, where an m-order spacing would be defined as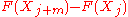

Multivariate distributions

discuss extended maximum spacing methods to the multivariate case. As there is no natural order for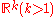

, they discuss two alternative approaches: a geometric approach based on Dirichlet cells and a probabilistic approach based on a “nearest neighbor ball” metric.

History and usage

Definition

Example 1

Example 2

Consistency and efficiency

Sensitivity

Goodness of fit

Alternate measures and spacings

Multivariate distributions

See also

Works Cited