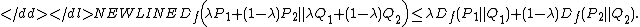F-divergence
Encyclopedia
In probability theory
, an ƒ-divergence is a function Df(P || Q) that measures the difference between two probability distributions P and Q. The divergence is intuitively an average, weighted by the function f, of the odds ratio
given by P and Q.
These divergences were introduced and studied independently by , and and are sometimes known as Csiszár ƒ-divergences, Csiszár-Morimoto divergences or Ali-Silvey distances.
f such that f(1) = 0, the f-divergence of Q from P is
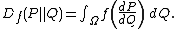
If P and Q are both absolutely continuous with respect to a reference distribution μ on Ω then their probability densities p and q satisfy dP = p dμ and dQ = q dμ. In this case the f-divergence can be written as
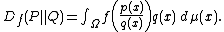
, and total variation distance, are special cases of f-divergence, coinciding with a particular choice of f. The following table lists many of the common divergences between probability distributions and the f function to which they correspond (cf. ).
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, an ƒ-divergence is a function Df(P || Q) that measures the difference between two probability distributions P and Q. The divergence is intuitively an average, weighted by the function f, of the odds ratio
Odds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
given by P and Q.
These divergences were introduced and studied independently by , and and are sometimes known as Csiszár ƒ-divergences, Csiszár-Morimoto divergences or Ali-Silvey distances.
Definition
Let P and Q be two probability distributions over a space Ω such that P is absolutely continuous with respect to Q. Then, for a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
f such that f(1) = 0, the f-divergence of Q from P is
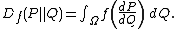
If P and Q are both absolutely continuous with respect to a reference distribution μ on Ω then their probability densities p and q satisfy dP = p dμ and dQ = q dμ. In this case the f-divergence can be written as
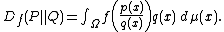
Instances of f-divergences
Many common divergences, such as KL-divergence, Hellinger distanceHellinger distance
In probability and statistics, the Hellinger distance is used to quantify the similarity between two probability distributions. It is a type of f-divergence...
, and total variation distance, are special cases of f-divergence, coinciding with a particular choice of f. The following table lists many of the common divergences between probability distributions and the f function to which they correspond (cf. ).
| Divergence | Corresponding f(t) |
|---|---|
| KL-divergence |  |
| Hellinger distance Hellinger distance In probability and statistics, the Hellinger distance is used to quantify the similarity between two probability distributions. It is a type of f-divergence... |
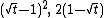 |
| Total variation distance | |
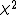 -divergence -divergence |
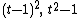 |
| α-divergence | 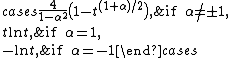 |
Properties
- Non-negativity: the ƒ-divergence is always positive, and equal to zero if and only if the measures P and Q coincide. This follows immediately from the Jensen’s inequality:
-
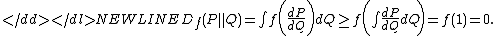
- Monotonicity: if κ is an arbitrary transition probability that transforms measures P and Q into Pκ and Qκ correspondingly, then
-
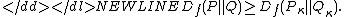
The equality here holds if and only if the transition is induced from a sufficient statistic with respect to {P, Q}.
- Convexity: for any
- Convexity: for any
- Monotonicity: if κ is an arbitrary transition probability that transforms measures P and Q into Pκ and Qκ correspondingly, then
-