
Probability integral transform
Encyclopedia
In statistics
, the probability integral transform or transformation relates to the result that data values that are modelled as being random variable
s from any given continuous distribution can be converted to random variables having a uniform distribution
. This holds exactly provided that the distribution being used is the true distribution of the random variables; if the distribution is one fitted to the data the result will hold approximately in large samples.
is F. Then the random variable Y defined as

has a uniform distribution.
For an illustrative example, let X be a random variable with a standard normal distribution N(0,1). Then its CDF is
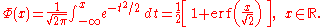
Then the new random variable Y, defined by Y=Φ(X), is uniformly distributed.
is to provide the basis for testing whether a set of observations can reasonably be modelled as arising from a specified distribution. Specifically, the probability integral transform is applied to construct an equivalent set of values, and a test is then made of whether a uniform distribution is appropriate for the constructed dataset. Examples of this are P-P plots and Kolmogorov-Smirnov test
s.
A second use for the transformation is in the theory related to copulas
which are a means of both defining and working with distributions for statistically dependent multivariate data.
A third use is based on applying the inverse of the probability integral transform to convert random variables from a uniform distribution to have a selected distribution: this is known as inverse transform sampling.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the probability integral transform or transformation relates to the result that data values that are modelled as being random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s from any given continuous distribution can be converted to random variables having a uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
. This holds exactly provided that the distribution being used is the true distribution of the random variables; if the distribution is one fitted to the data the result will hold approximately in large samples.
Implementation
Suppose that a random variable X has a continuous distribution for which the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is F. Then the random variable Y defined as

has a uniform distribution.
For an illustrative example, let X be a random variable with a standard normal distribution N(0,1). Then its CDF is
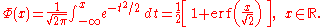
Then the new random variable Y, defined by Y=Φ(X), is uniformly distributed.
Applications
One use for the probability integral transform in statistical data analysisData analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
is to provide the basis for testing whether a set of observations can reasonably be modelled as arising from a specified distribution. Specifically, the probability integral transform is applied to construct an equivalent set of values, and a test is then made of whether a uniform distribution is appropriate for the constructed dataset. Examples of this are P-P plots and Kolmogorov-Smirnov test
Kolmogorov-Smirnov test
In statistics, the Kolmogorov–Smirnov test is a nonparametric test for the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution , or to compare two samples...
s.
A second use for the transformation is in the theory related to copulas
Copula (statistics)
In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
which are a means of both defining and working with distributions for statistically dependent multivariate data.
A third use is based on applying the inverse of the probability integral transform to convert random variables from a uniform distribution to have a selected distribution: this is known as inverse transform sampling.

