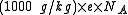Mass-to-charge ratio
Encyclopedia
The mass-to-charge ratio ratio (m/Q) is a physical quantity
that is widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics
. It appears in the scientific fields of lithography
, electron microscopy, cathode ray tube
s, accelerator physics
, nuclear physics
, Auger spectroscopy, cosmology
and mass spectrometry
. The importance of the mass-to-charge ratio, according to classical electrodynamics, is that two particles with the same mass-to-charge ratio move in the same path in a vacuum when subjected to the same electric and magnetic fields.
Some fields use the charge-to-mass ratio (Q/m) instead, which is the multiplicative inverse
of the mass-to-charge ratio. The 2006 CODATA recommended value is e⁄me = 1.758820150(44)×10^11 C/kg.[6].
where F is the force
applied to the ion, m is the mass
of the particle, a is the acceleration
, Q is the electric charge
, E is the electric field
, and v x B is the cross product
of the ion's velocity
and the magnetic field
.
This differential equation is the classic equation of motion for charged particles. Together with the particle's initial conditions, it completely determines the particle's motion in space and time in terms of m/Q. Thus mass spectrometers could be thought of as "mass-to-charge spectrometers". When presenting data in a mass spectrum
, it is common to use the dimensionless m/z, which denotes the dimensionless quantity formed by dividing the mass number of the ion by its charge number.
Combining the two previous equation yields:
This differential equation is the classic equation of motion of a charged particle in vacuum. Together with the particle's initial conditions it determines the particle's motion in space and time. It immediately reveals that two particles with the same m/Q ratio behave in the same way. This is why the mass-to-charge ratio is an important physical quantity in those scientific fields where charged particles interact with magnetic or electric fields.
, such as the Stern–Gerlach effect
that can diverge the path of ions of identical m/Q.
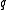 is also very common. Charge is a scalar property, meaning that it can be either positive (+ symbol) or negative (- symbol). Sometimes, however, the sign of the charge is indicated indirectly. Coulomb is the SI unit of charge; however, other units are not uncommon.
is also very common. Charge is a scalar property, meaning that it can be either positive (+ symbol) or negative (- symbol). Sometimes, however, the sign of the charge is indicated indirectly. Coulomb is the SI unit of charge; however, other units are not uncommon.
The SI unit of the physical quantity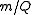 is kilograms per coulomb.
is kilograms per coulomb.
. This notation eases data interpretation since it is numerically more related to the unified atomic mass unit of the analyte. The m in m/z is representative of molecular or atomic mass and z is representative of the number of elementary charges carried by the ion. Thus a molecule of 1000 Da carrying two charges will be observed at m/z 500. These notations are closely related through the unified atomic mass unit and the elementary charge
.
Although it is rarely done the numerical conversion factor from SI units (kg/C) to m/z notation is:
where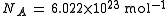
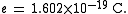
was first measured by J. J. Thomson
. By doing this he showed that the electron—postulated earlier to explain electricity—was in fact a particle with a mass and a charge; and that its mass-to-charge ratio was much smaller than that of the hydrogen ion H+. In 1898 Wilhelm Wien
separated ions (canal rays) according to their mass-to-charge ratio with an ion optical device with superimposed electric and magnetic fields (Wien filter
). In 1901 Walter Kaufman
measured the relativistic mass increase of fast electrons. In 1913, Thomson measured the mass-to-charge ratio of ion
s with an instrument he called a parabola spectrograph. Today, an instrument that measures the mass-to-charge ratio of charged particles is called a mass spectrometer.
of an object divided by the mass of the same object. This quantity is generally useful only for objects that may be treated as particles. For extended objects, total charge, charge density, total mass, and mass density are often more useful.
Often, the charge-to-mass ratio can be determined from observing the deflection of a charged particle in an external magnetic field. The cyclotron
equation, combined with other information such as the kinetic energy
of the particle, will give the charge-to-mass ratio. One application of this principle is the mass spectrometer. The same principle can be used to extract information in experiments involving the Wilson cloud chamber.
The ratio of electrostatic to gravitational forces between two particles will be proportional to the product of their charge-to-mass ratios. It turns out that gravitational forces are negligible on the subatomic level. This is due to the extremely small masses of the subatomic particles.
in 1897—and more successfully by Dunnington, which involves the angular momentum
and deflection due to a perpendicular magnetic field
. Thomson's measurement convinced him that cathode ray
s were particles, which were later identified as electron
s, and is generally credited with their discovery.
The 2006 CODATA
recommended value is = . CODATA refers to this as the electron charge-to-mass quotient, but ratio is still commonly used.
There are two other common ways of measuring the charge to mass ratio of an electron, apart from Thomson and Dunnington's methods.
, which gives rise to energy splittings in the presence of a magnetic field
B:
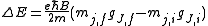
Here mj are quantum integer values ranging from -j to j, with j as the eigenvalue of the total angular momentum operator
J, with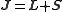
where S is the spin operator
with eigenvalue s and L is the angular momentum operator
with eigenvalue l. gJ is the Landé g-factor
, calculated as
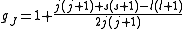
The shift in energy is also given in terms of frequency
ν and wavelength
λ as

Measurements of the Zeeman effect commonly involve the use of a Fabry–Pérot interferometer, with light from a source (placed in a magnetic field) being passed between two mirrors of the interferometer. If δD is the change in mirror separation required to bring the mth-order ring of wavelength λ + Δλ into coincidence with that of wavelength λ, and ΔD brings the (m + 1)th ring of wavelength λ into coincidence with the mth-order ring, then
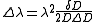 .
.
It follows then that
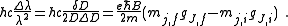
Rearranging, it is possible to solve for the charge-to-mass ratio of an electron as
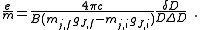
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
that is widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics
Ion optics
Ion optics involves the focusing of plasmas and ion streams, usually in mass spectrometry.-Electric field manipulation:* Electrostatic lens** Einzel lens* Electrostatic analyzer...
. It appears in the scientific fields of lithography
Lithography
Lithography is a method for printing using a stone or a metal plate with a completely smooth surface...
, electron microscopy, cathode ray tube
Cathode ray tube
The cathode ray tube is a vacuum tube containing an electron gun and a fluorescent screen used to view images. It has a means to accelerate and deflect the electron beam onto the fluorescent screen to create the images. The image may represent electrical waveforms , pictures , radar targets and...
s, accelerator physics
Accelerator physics
Accelerator physics deals with the problems of building and operating particle accelerators.The experiments conducted with particle accelerators are not regarded as part of accelerator physics. These belong to particle physics, nuclear physics, condensed matter physics, materials physics, etc...
, nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
, Auger spectroscopy, cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
and mass spectrometry
Mass spectrometry
Mass spectrometry is an analytical technique that measures the mass-to-charge ratio of charged particles.It is used for determining masses of particles, for determining the elemental composition of a sample or molecule, and for elucidating the chemical structures of molecules, such as peptides and...
. The importance of the mass-to-charge ratio, according to classical electrodynamics, is that two particles with the same mass-to-charge ratio move in the same path in a vacuum when subjected to the same electric and magnetic fields.
Some fields use the charge-to-mass ratio (Q/m) instead, which is the multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the mass-to-charge ratio. The 2006 CODATA recommended value is e⁄me = 1.758820150(44)×10^11 C/kg.[6].
Origin
When charged particles move in electric and magnetic fields the following two laws apply: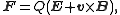 |
(Lorentz force Lorentz force In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:... law) |
|
 |
(Newton's second law of motion) | |
where F is the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
applied to the ion, m is the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the particle, a is the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, Q is the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, E is the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, and v x B is the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the ion's velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
.
This differential equation is the classic equation of motion for charged particles. Together with the particle's initial conditions, it completely determines the particle's motion in space and time in terms of m/Q. Thus mass spectrometers could be thought of as "mass-to-charge spectrometers". When presenting data in a mass spectrum
Mass spectrum
A mass spectrum is an intensity vs. m/z plot representing a chemical analysis. Hence, the mass spectrum of a sample is a pattern representing the distribution of ions by mass in a sample. It is a histogram usually acquired using an instrument called a mass spectrometer...
, it is common to use the dimensionless m/z, which denotes the dimensionless quantity formed by dividing the mass number of the ion by its charge number.
Combining the two previous equation yields:
-
 .
.
This differential equation is the classic equation of motion of a charged particle in vacuum. Together with the particle's initial conditions it determines the particle's motion in space and time. It immediately reveals that two particles with the same m/Q ratio behave in the same way. This is why the mass-to-charge ratio is an important physical quantity in those scientific fields where charged particles interact with magnetic or electric fields.
Exceptions
There are non-classical effects that derive from quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, such as the Stern–Gerlach effect
Stern–Gerlach experiment
Important in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
that can diverge the path of ions of identical m/Q.
Symbols and units
The IUPAC recommended symbol for mass is m. The IUPAC recommended symbol for charge is Q; however,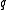 is also very common. Charge is a scalar property, meaning that it can be either positive (+ symbol) or negative (- symbol). Sometimes, however, the sign of the charge is indicated indirectly. Coulomb is the SI unit of charge; however, other units are not uncommon.
is also very common. Charge is a scalar property, meaning that it can be either positive (+ symbol) or negative (- symbol). Sometimes, however, the sign of the charge is indicated indirectly. Coulomb is the SI unit of charge; however, other units are not uncommon.The SI unit of the physical quantity
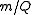 is kilograms per coulomb.
is kilograms per coulomb.
-
 = kg/C
= kg/C
Mass spectrometry
The units and notation above are used when dealing with the physics of mass spectrometry; however, the unitless m/z notation is used for the independent variable in a mass spectrumMass spectrum
A mass spectrum is an intensity vs. m/z plot representing a chemical analysis. Hence, the mass spectrum of a sample is a pattern representing the distribution of ions by mass in a sample. It is a histogram usually acquired using an instrument called a mass spectrometer...
. This notation eases data interpretation since it is numerically more related to the unified atomic mass unit of the analyte. The m in m/z is representative of molecular or atomic mass and z is representative of the number of elementary charges carried by the ion. Thus a molecule of 1000 Da carrying two charges will be observed at m/z 500. These notations are closely related through the unified atomic mass unit and the elementary charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
.
Although it is rarely done the numerical conversion factor from SI units (kg/C) to m/z notation is:
where
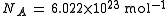
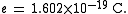
History
In the 19th century the mass-to-charge ratios of some ions were measured by electrochemical methods. In 1897 the mass-to-charge ratio, , of the electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
was first measured by J. J. Thomson
J. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
. By doing this he showed that the electron—postulated earlier to explain electricity—was in fact a particle with a mass and a charge; and that its mass-to-charge ratio was much smaller than that of the hydrogen ion H+. In 1898 Wilhelm Wien
Wilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
separated ions (canal rays) according to their mass-to-charge ratio with an ion optical device with superimposed electric and magnetic fields (Wien filter
Wien filter
A Wien filter is a device consisting of perpendicular electric and magnetic fields that can be used as a velocity filter for charged particles, for example in electron microscopes and spectrometers. It is named for Wilhelm Wien who developed it in 1898 for the study of anode rays. It can be...
). In 1901 Walter Kaufman
Walter Kaufmann (physicist)
Walter Kaufmann was a German physicist. He is most well known for his first experimental proof of the velocity dependence of mass, which was an important contribution to the development of modern physics, including special relativity.-Life:In 1890/91 he studied mechanical engineering at the...
measured the relativistic mass increase of fast electrons. In 1913, Thomson measured the mass-to-charge ratio of ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s with an instrument he called a parabola spectrograph. Today, an instrument that measures the mass-to-charge ratio of charged particles is called a mass spectrometer.
Charge-to-mass ratio
The charge-to-mass ratio (Q/m) of an object is, as its name implies, the chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of an object divided by the mass of the same object. This quantity is generally useful only for objects that may be treated as particles. For extended objects, total charge, charge density, total mass, and mass density are often more useful.
Significance
In some experiments, the charge-to-mass ratio is the only quantity that can be measured directly. Often, the charge can be inferred from theoretical considerations, so that the charge-to-mass ratio provides a way to calculate the mass of a particle.Often, the charge-to-mass ratio can be determined from observing the deflection of a charged particle in an external magnetic field. The cyclotron
Cyclotron
In technology, a cyclotron is a type of particle accelerator. In physics, the cyclotron frequency or gyrofrequency is the frequency of a charged particle moving perpendicularly to the direction of a uniform magnetic field, i.e. a magnetic field of constant magnitude and direction...
equation, combined with other information such as the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the particle, will give the charge-to-mass ratio. One application of this principle is the mass spectrometer. The same principle can be used to extract information in experiments involving the Wilson cloud chamber.
The ratio of electrostatic to gravitational forces between two particles will be proportional to the product of their charge-to-mass ratios. It turns out that gravitational forces are negligible on the subatomic level. This is due to the extremely small masses of the subatomic particles.
The electron
The elementary charge-to-electron mass quotient, , is a quantity in experimental physics. It matters because the electron mass me is difficult to measure directly, and is instead derived from measurements of the elementary charge e and . It also has historical significance: the Q/m ratio of the electron was successfully calculated by J. J. ThomsonJ. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
in 1897—and more successfully by Dunnington, which involves the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and deflection due to a perpendicular magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. Thomson's measurement convinced him that cathode ray
Cathode ray
Cathode rays are streams of electrons observed in vacuum tubes. If an evacuated glass tube is equipped with two electrodes and a voltage is applied, the glass opposite of the negative electrode is observed to glow, due to electrons emitted from and travelling perpendicular to the cathode Cathode...
s were particles, which were later identified as electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s, and is generally credited with their discovery.
The 2006 CODATA
Committee on Data for Science and Technology
The Committee on Data for Science and Technology was established in 1966 as an interdisciplinary committee of the International Council for Science. It seeks to improve the compilation, critical evaluation, storage, and retrieval of data of importance to science and technology.The CODATA Task...
recommended value is = . CODATA refers to this as the electron charge-to-mass quotient, but ratio is still commonly used.
There are two other common ways of measuring the charge to mass ratio of an electron, apart from Thomson and Dunnington's methods.
- The Magnetron Method: Using a GRD7 Valve (Ferranti valveFerranti valveThe Ferranti valve is a type of vacuum tube developed by Messers. Ferranti Education ltd in measuring the charge to mass ratio of an electron. It consists of an anode and two co-axial guard rings. A cathode, a thin wire of tungsten filament, runs through this arrangement. When heated to a...
), electrons are expelled from a hot tungsten-wire filament towards an anode. The electron is then deflected using a solenoid. From the current in the solenoid and the current in the Ferranti Valve, e/m can be calculated. - Fine Beam Tube Method: Electrons are accelerated from a cathode to a cap-shaped anode. The electron is then expelled into a helium-filled ray tube, producing a luminous circle. From the radius of this circle, e/m is calculated.
Zeeman Effect
The charge-to-mass ratio of an electron may also be measured with the Zeeman effectZeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
, which gives rise to energy splittings in the presence of a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B:
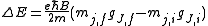
Here mj are quantum integer values ranging from -j to j, with j as the eigenvalue of the total angular momentum operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
J, with
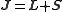
where S is the spin operator
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
with eigenvalue s and L is the angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
with eigenvalue l. gJ is the Landé g-factor
Landé g-factor
In physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921....
, calculated as
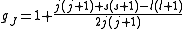
The shift in energy is also given in terms of frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ν and wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ as

Measurements of the Zeeman effect commonly involve the use of a Fabry–Pérot interferometer, with light from a source (placed in a magnetic field) being passed between two mirrors of the interferometer. If δD is the change in mirror separation required to bring the mth-order ring of wavelength λ + Δλ into coincidence with that of wavelength λ, and ΔD brings the (m + 1)th ring of wavelength λ into coincidence with the mth-order ring, then
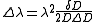 .
.It follows then that
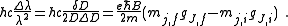
Rearranging, it is possible to solve for the charge-to-mass ratio of an electron as
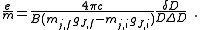
External links
- BIPM SI brochure
- AIP style manual
- NIST on units and manuscript check list
- Physics Today's instructions on quantities and units