Magnetogyric ratio
Encyclopedia
In physics
, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio
of its magnetic dipole moment to its angular momentum
, and it is often denoted by the symbol γ
, gamma. Its SI
units are radian
per second
per tesla
(s−1·T -1) or, equivalently, coulomb per kilogram
(C·kg−1).
The term "gyromagnetic ratio" is sometimes used as a synonym for a different but closely related quantity, the g-factor. The g-factor, unlike the gyromagnetic ratio, is dimensionless. For more on the g-factor, see below, or see the article g-factor.
, or an electron
, when placed in an external magnetic field
B (measured in teslas) that is not aligned with its magnetic moment
, will precess
at a frequency
f (measured in hertz
), that is proportional to the external field: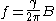
.
For this reason, values of γ/(2π), in units of hertz
per tesla
(Hz/T), are often quoted instead of γ.
This relationship also explains an apparent contradiction between the two equivalent terms, gyromagnetic ratio versus magnetogyric ratio: whereas it is a ratio of a magnetic property (i.e. dipole moment
) to a gyric (rotational, from Greek
: γύρος, "turn") property (i.e. angular momentum
), it is also, at the same time, a ratio between the angular precession frequency
(another gyric property) ω = 2πf and the magnetic field
.
body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment and an angular momentum due to its rotation. It can be shown that as long as its charge and mass are distributed identically (e.g., both distributed uniformly), its gyromagnetic ratio is
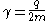
where q is its charge and m is its mass. The derivation of this relation is as follows:
It suffices to demonstrate this for an infinitesimally narrow circular ring within the body, as the general result follows from an integration
. Suppose the ring has radius r, area A = πr2, mass m, charge q, and angular momentum L=mvr. Then the magnitude of the magnetic dipole moment is
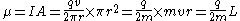
as desired.
. While an electron's spin is sometimes visualized as a literal rotation about an axis, it is in fact a fundamentally different, quantum-mechanical phenomenon with no true analogue in classical physics. Consequently, there is no reason to expect the above classical relation to hold. In fact it does not, giving the wrong result by a dimensionless factor called the electron g-factor, denoted ge (or just g when there is no risk of confusion):
where μB is the Bohr magneton. As mentioned above, in classical physics one would expect the g-factor to be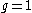
. However in the framework of relativistic quantum mechanics,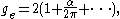
where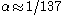
is the fine-structure constant
. Here the small corrections to the relativistic result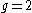
come from the quantum field theory. Experimentally, the electron g-factor has been measured to twelve decimal places:
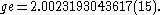
The electron gyromagnetic ratio is given by NIST as
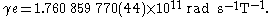
The g-factor and γ are in excellent agreement with theory; see Precision tests of QED
for details.
2 is a consequence of relativity; it is not. The factor 2 can be obtained from the linearization of both the Schrödinger equation
and the relativistic Klein-Gordon equation
(which leads to Dirac's). In both cases a 4-spinor
is obtained and for both linearizations the g-factor
is found to be equal to 2; Therefore, the factor 2 is a consequence of the wave equation dependency on the first (and not the second) derivatives with respect to space and time.
s, neutrons, and many nuclei carry nuclear spin, which gives rise to a gyromagnetic ratio as above. The ratio is conventionally written in terms of the proton mass and charge, even for neutrons and for other nuclei, for the sake of simplicity and consistency. The formula is:
where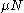
is the nuclear magneton, and g is the g-factor of the nucleon or nucleus in question.
The gyromagnetic ratio of a nucleus is particularly important because of the role it plays in Nuclear Magnetic Resonance
(NMR) and Magnetic Resonance Imaging
(MRI). These procedures rely on the fact that nuclear spins precess in a magnetic field at a rate called the Larmor frequency, which is simply the product of the gyromagnetic ratio with the magnetic field strength.
Approximate values for some common nuclei are given in the Table below.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of its magnetic dipole moment to its angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, and it is often denoted by the symbol γ
Gamma
Gamma is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. It was derived from the Phoenician letter Gimel . Letters that arose from Gamma include the Roman C and G and the Cyrillic letters Ge Г and Ghe Ґ.-Greek:In Ancient Greek, gamma represented a...
, gamma. Its SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units are radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
per second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
per tesla
Tesla (unit)
The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
(s−1·T -1) or, equivalently, coulomb per kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
(C·kg−1).
The term "gyromagnetic ratio" is sometimes used as a synonym for a different but closely related quantity, the g-factor. The g-factor, unlike the gyromagnetic ratio, is dimensionless. For more on the g-factor, see below, or see the article g-factor.
Gyromagnetic ratio and Larmor precession
Any free system with a constant gyromagnetic ratio, such as a rigid system of charges, a nucleusAtomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
, or an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, when placed in an external magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B (measured in teslas) that is not aligned with its magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
, will precess
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
at a frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
f (measured in hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
), that is proportional to the external field:
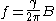.For this reason, values of γ/(2π), in units of hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
per tesla
Tesla (unit)
The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
(Hz/T), are often quoted instead of γ.
This relationship also explains an apparent contradiction between the two equivalent terms, gyromagnetic ratio versus magnetogyric ratio: whereas it is a ratio of a magnetic property (i.e. dipole moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
) to a gyric (rotational, from Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
: γύρος, "turn") property (i.e. angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
), it is also, at the same time, a ratio between the angular precession frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
(another gyric property) ω = 2πf and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
.
Gyromagnetic ratio for a classical rotating body
Consider a chargedElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment and an angular momentum due to its rotation. It can be shown that as long as its charge and mass are distributed identically (e.g., both distributed uniformly), its gyromagnetic ratio is
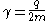
where q is its charge and m is its mass. The derivation of this relation is as follows:
It suffices to demonstrate this for an infinitesimally narrow circular ring within the body, as the general result follows from an integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. Suppose the ring has radius r, area A = πr2, mass m, charge q, and angular momentum L=mvr. Then the magnitude of the magnetic dipole moment is
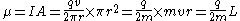
as desired.
Gyromagnetic ratio for an isolated electron
An isolated electron has an angular momentum and a magnetic moment resulting from its spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
. While an electron's spin is sometimes visualized as a literal rotation about an axis, it is in fact a fundamentally different, quantum-mechanical phenomenon with no true analogue in classical physics. Consequently, there is no reason to expect the above classical relation to hold. In fact it does not, giving the wrong result by a dimensionless factor called the electron g-factor, denoted ge (or just g when there is no risk of confusion):
where μB is the Bohr magneton. As mentioned above, in classical physics one would expect the g-factor to be
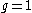. However in the framework of relativistic quantum mechanics,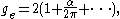where
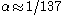is the fine-structure constantFine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
. Here the small corrections to the relativistic result
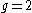come from the quantum field theory. Experimentally, the electron g-factor has been measured to twelve decimal places: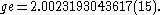The electron gyromagnetic ratio is given by NIST as
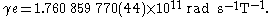
The g-factor and γ are in excellent agreement with theory; see Precision tests of QED
Precision tests of QED
Quantum electrodynamics , a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics....
for details.
Gyromagnetic factor as a consequence of relativity
Since a gyromagnetic factor equal to 2 follows from the Dirac's equation it is a frequent misconception to think that a g-factorG-factor
A g-factor is a dimensionless quantity which characterizes the magnetic moment and gyromagnetic ratio of a particle or nucleus...
2 is a consequence of relativity; it is not. The factor 2 can be obtained from the linearization of both the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
and the relativistic Klein-Gordon equation
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
(which leads to Dirac's). In both cases a 4-spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
is obtained and for both linearizations the g-factor
G-factor
A g-factor is a dimensionless quantity which characterizes the magnetic moment and gyromagnetic ratio of a particle or nucleus...
is found to be equal to 2; Therefore, the factor 2 is a consequence of the wave equation dependency on the first (and not the second) derivatives with respect to space and time.
Gyromagnetic ratio for a nucleus
ProtonProton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, neutrons, and many nuclei carry nuclear spin, which gives rise to a gyromagnetic ratio as above. The ratio is conventionally written in terms of the proton mass and charge, even for neutrons and for other nuclei, for the sake of simplicity and consistency. The formula is:
where
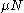is the nuclear magneton, and g is the g-factor of the nucleon or nucleus in question.The gyromagnetic ratio of a nucleus is particularly important because of the role it plays in Nuclear Magnetic Resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(NMR) and Magnetic Resonance Imaging
Magnetic resonance imaging
Magnetic resonance imaging , nuclear magnetic resonance imaging , or magnetic resonance tomography is a medical imaging technique used in radiology to visualize detailed internal structures...
(MRI). These procedures rely on the fact that nuclear spins precess in a magnetic field at a rate called the Larmor frequency, which is simply the product of the gyromagnetic ratio with the magnetic field strength.
Approximate values for some common nuclei are given in the Table below.
| Nucleus | γ / 106 rad s−1 T−1 | γ/2π / MHz T−1 |
|---|---|---|
| 1H Proton The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number.... |
267.513 | 42.576 |
| 2H | 41.065 | 6.536 |
| 3He | -203.789 | -32.434 |
| 7Li | 103.962 | 16.546 |
| 13C Carbon-13 Carbon-13 is a natural, stable isotope of carbon and one of the environmental isotopes. It makes up about 1.1% of all natural carbon on Earth.- Detection by mass spectrometry :... |
67.262 | 10.705 |
| 14N | 19.331 | 3.077 |
| 15N | -27.116 | -4.316 |
| 17O Oxygen-17 Oxygen-17 is a low abundant isotope of oxygen . Being the only stable isotope of oxygen possessing a nuclear spin and the unique characteristic of field-independent relaxation it enables NMR studies of metabolic pathways of compounds incorporating oxygen at high magnetic fields Oxygen-17 is a low... |
-36.264 | -5.772 |
| 19F | 251.662 | 40.053 |
| 23Na | 70.761 | 11.262 |
| 31P Phosphor A phosphor, most generally, is a substance that exhibits the phenomenon of luminescence. Somewhat confusingly, this includes both phosphorescent materials, which show a slow decay in brightness , and fluorescent materials, where the emission decay takes place over tens of nanoseconds... |
108.291 | 17.235 |
| 129Xe | -73.997 | -11.777 |
See also
- Dirac EquationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
- Landé g-factorLandé g-factorIn physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921....
- NMRNMRNMR may refer to:Applications of Nuclear Magnetic Resonance:* Nuclear magnetic resonance* NMR spectroscopy* Solid-state nuclear magnetic resonance* Protein nuclear magnetic resonance spectroscopy* Proton NMR* Carbon-13 NMR...
- Chemical shiftChemical shiftIn nuclear magnetic resonance spectroscopy, the chemical shift is the resonant frequency of a nucleus relative to a standard. Often the position and number of chemical shifts are diagnostic of the structure of a molecule...
- Larmor equation
- Proton–gyromagnetic ratio