
Magnetic circuit
Encyclopedia
A magnetic circuit is made up of one or more closed loop paths containing a magnetic flux
. The flux is usually generated by permanent magnets or electromagnet
s and confined to the path by magnetic core
s consisting of ferromagnetic materials like iron, although there may be air gaps or other materials in the path. Magnetic circuits are employed to efficiently channel magnetic field
s in many devices such as electric motor
s, generators, transformer
s, relay
s, lifting electromagnet
s, SQUID
s, galvanometer
s, and magnetic recording head
s.
The concept of a "magnetic circuit" exploits a one-to-one correspondence between the equations of the magnetic field in an unsaturated ferromagnetic material to that of an electrical circuit. Using this concept the magnetic fields of complex devices such as transformer
s can be quickly solved using the methods and techniques developed for electrical circuits.
Some examples of magnetic circuits are:
drives a current of electrical charge in electrical circuits, magnetomotive force
(MMF) 'drives' magnetic flux through magnetic circuits. The term 'magnetomotive force', though, is a misnomer since it is not a force nor is anything moving. It is perhaps better to call it simply MMF. In analogy to the definition of EMF
, the magnetomotive force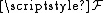 around a closed loop is defined as:
around a closed loop is defined as:

The MMF represents the potential that a hypothetical magnetic charge
would gain by completing the loop. The magnetic flux that is driven is not a current of magnetic charge; it merely has the same relationship to MMF that electric current has to EMF. (See microscopic origins of reluctance below for a further description.)
The unit of magnetomotive force is the ampere-turn
(At), represented by a steady, direct electric current
of one ampere
flowing in a single-turn loop of electrically conducting material in a vacuum
. The gilbert (Gi), established by the IEC
in 1930 http://www.iec.ch/about/history/, is the CGS unit of magnetomotive force and is a slightly smaller unit than the ampere-turn. The unit is named after William Gilbert (1544–1603) English physician and natural philosopher.
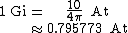
The magnetomotive force can often be quickly calculated using Ampère's law. For example, the magnetomotive force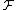 of long coil is:
of long coil is:
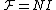 ,
,
where N is the number of turns
and I is the current in the coil. In practice this equation is used for the MMF of real inductors with N being the winding number
of the inducting coil.
through the magnetic components of the system. The magnetic flux through a magnetic component is proportional to the number of magnetic field lines that pass through the cross sectional area of that component. This is the net number, i.e. the number passing through in one direction, minus the number passing through in the other direction. The direction of the magnetic field vector B is by definition from the south to the north pole of a magnet inside the magnet; outside the field lines go from north to south.
The flux
through an element of area
perpendicular
to the direction of magnetic field is given by the product of the magnetic field
and the area
element. More generally, magnetic flux Φ is defined by a scalar product of the magnetic field and the area element vector. Quantitatively, the magnetic flux through a surface S is defined as the integral
of the magnetic field over the area of the surface
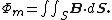
For a magnetic component the area S used to calculate the magnetic flux Φ is usually chosen to be the cross-sectional area of the component.
The SI
unit of magnetic flux is the weber
(in derived units: volt-seconds), and the unit of magnetic field is the weber per square meter, or tesla
.
is an empirical relation between the EMF
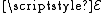 applied across an element and the current I it generates through that element. It is written as:
applied across an element and the current I it generates through that element. It is written as:
where R is the electrical resistance
of that material. Hopkinson's law is a counterpart to Ohm's law
used in magnetic circuits. The law is named after the British electrical engineer, John Hopkinson
. It states that
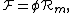
where is the magnetomotive force (MMF) across a magnetic element,
is the magnetomotive force (MMF) across a magnetic element, 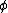 is the magnetic flux
is the magnetic flux
through the magnetic element, and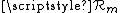 is the magnetic reluctance of that element. (It shall be shown later that this relationship is due to the empirical relationship between the H-field and the magnetic field B, B=μH, where μ is the permeability
is the magnetic reluctance of that element. (It shall be shown later that this relationship is due to the empirical relationship between the H-field and the magnetic field B, B=μH, where μ is the permeability
of the material.) Like Ohm's law, Hopkinson's law can be interpreted either as an empirical equation that works for some materials, or it may serve as a definition of reluctance.
in an electrical circuit
(although it does not dissipate magnetic energy). In likeness to the way an electric field
causes an electric current
to follow the path of least resistance
, a magnetic field
causes magnetic flux
to follow the path of least magnetic reluctance. It is a scalar
,
extensive quantity, akin to electrical resistance.
The total reluctance is equal to the ratio of the (MMF) in a passive magnetic circuit and the magnetic flux
in this circuit. In an AC field, the reluctance is the ratio of the amplitude values for a sinusoidal MMF and magnetic flux. (see phasors)
The definition can be expressed as:

where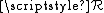 is the reluctance in ampere-turn
is the reluctance in ampere-turn
s per weber
(a unit that is equivalent to turns per henry).
Magnetic flux always forms a closed loop, as described by Maxwell's equations
, but the path of the loop depends on the reluctance of the surrounding materials. It is concentrated around the path of least reluctance. Air and vacuum have high reluctance, while easily magnetized materials such as soft iron have low reluctance. The concentration of flux in low-reluctance materials forms strong temporary poles and causes mechanical forces that tend to move the materials towards regions of higher flux so it is always an attractive force(pull).
The inverse of reluctance is called permeance.

Its SI
derived unit is the henry (the same as the unit of inductance
, although the two concepts are distinct).

where
s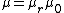 is the permeability
is the permeability
of the material (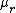 is the relative permeability of the material (dimensionless), and
is the relative permeability of the material (dimensionless), and 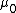 is the permeability of free space)
is the permeability of free space)
A is the cross-sectional area of the circuit in square metre
s
This is similar to the equation for electrical resistance in materials, with permeability being analogous to conductivity; the reciprocal of the permeability is known as magnetic reluctivity and is analogous to resistivity. Longer, thinner geometries with low permeabilities lead to higher reluctance. Low reluctance, like low resistance in electric circuits, is generally preferred.
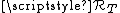 of reluctances
of reluctances 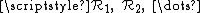 in series is:
in series is:
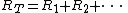
This also follows from Ampère's law
and is analogous to Kirchhoff's voltage law
for adding resistances in series. Also, the sum of magnetic fluxes into any node is always zero:
into any node is always zero:
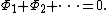
This follows from Gauss's law
and is analogous to Kirchhoff's current law
for analyzing electrical circuits.
Together, the three laws above form a complete system for analysing magnetic circuits, in a manner similar to electric circuits. Comparing the two types of circuits shows that:
Magnetic circuits can be solved for the flux in each branch by application of the magnetic equivalent of Kirchhoff's Voltage Law
(KVL) for pure source/resistance circuits. Specifically, whereas KVL states that the voltage excitation applied to a loop is equal to the sum of the voltage drops (resistance times current) around the loop, the magnetic analogue states that the magnetomotive force (achieved from ampere-turn excitation) is equal to the sum of MMF drops (product of flux and reluctance) across the rest of the loop. (If there are multiple loops, the current in each branch can be solved through a matrix equation—much as a matrix solution for mesh circuit branch currents is obtained in loop analysis—after which the individual branch currents are obtained by adding and/or subtracting the constituent loop currents as indicated by the adopted sign convention and loop orientations.) Per Ampère's law
, the excitation is the product of the current and the number of complete loops made and is measured in ampere-turns. Stated more generally:
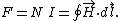
(Note that, per Stokes's theorem, the closed line integral
of H dot dl around a contour is equal to the open surface integral
of curl H dot dA across the surface bounded by the closed contour. Since, from Maxwell's equations
, curl H = J, the closed line integral of H dot dl evaluates to the total current passing through the surface. This is equal to the excitation, NI, which also measures current passing through the surface, thereby verifying that the net current flow through a surface is zero ampere-turns in a closed system that conserves energy.)
More complex magnetic systems, where the flux is not confined to a simple loop, must be analysed from first principles by using Maxwell's equations
.
. The notion of “magnetic resistance” was first mentioned by James Joule and the term "magnetomotive force
” (MMF) was first named by Bosanquet. The idea for a magnetic flux
law, similar to Ohm's law
for closed electric circuits, is attributed to H. Rowland
.
Reluctance can also be applied to:
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
. The flux is usually generated by permanent magnets or electromagnet
Electromagnet
An electromagnet is a type of magnet in which the magnetic field is produced by the flow of electric current. The magnetic field disappears when the current is turned off...
s and confined to the path by magnetic core
Magnetic core
A magnetic core is a piece of magnetic material with a high permeability used to confine and guide magnetic fields in electrical, electromechanical and magnetic devices such as electromagnets, transformers, electric motors, inductors and magnetic assemblies. It is made of ferromagnetic metal such...
s consisting of ferromagnetic materials like iron, although there may be air gaps or other materials in the path. Magnetic circuits are employed to efficiently channel magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s in many devices such as electric motor
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s, generators, transformer
Transformer
A transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
s, relay
Relay
A relay is an electrically operated switch. Many relays use an electromagnet to operate a switching mechanism mechanically, but other operating principles are also used. Relays are used where it is necessary to control a circuit by a low-power signal , or where several circuits must be controlled...
s, lifting electromagnet
Electromagnet
An electromagnet is a type of magnet in which the magnetic field is produced by the flow of electric current. The magnetic field disappears when the current is turned off...
s, SQUID
SQUID
A SQUID is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions....
s, galvanometer
Galvanometer
A galvanometer is a type of ammeter: an instrument for detecting and measuring electric current. It is an analog electromechanical transducer that produces a rotary deflection of some type of pointer in response to electric current flowing through its coil in a magnetic field. .Galvanometers were...
s, and magnetic recording head
Recording head
A recording head is the physical interface between a recording apparatus and a moving recording medium. Recording heads are generally classified according to the physical principle that allows them to impress their data upon their medium...
s.
The concept of a "magnetic circuit" exploits a one-to-one correspondence between the equations of the magnetic field in an unsaturated ferromagnetic material to that of an electrical circuit. Using this concept the magnetic fields of complex devices such as transformer
Transformer
A transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
s can be quickly solved using the methods and techniques developed for electrical circuits.
Some examples of magnetic circuits are:
- horseshoeHorseshoeA horseshoe, is a fabricated product, normally made of metal, although sometimes made partially or wholly of modern synthetic materials, designed to protect a horse's hoof from wear and tear. Shoes are attached on the palmar surface of the hooves, usually nailed through the insensitive hoof wall...
magnetMagnetA magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
with iron keeperMagnet keeperA magnet keeper is ferromagnetic bar placed across the poles of a permanent magnet that helps preserve the strength of the magnet by completing the magnetic circuit, and are particularly useful for magnets which have a low magnetic coercivity, such as AlNiCo magnets.Keepers also have a useful...
(low-reluctance circuit) - horseshoe magnet with no keeper (high-reluctance circuit)
- electric motorElectric motorAn electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
(variable-reluctance circuit)
Magnetomotive force (MMF)
Similar to the way that EMFElectromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
drives a current of electrical charge in electrical circuits, magnetomotive force
Magnetomotive force
Magnetomotive force is any physical driving force that produces magnetic flux. In this context, the expression "driving force" is used in a general sense of "work potential", and is analogous, but distinct from force measured in newtons...
(MMF) 'drives' magnetic flux through magnetic circuits. The term 'magnetomotive force', though, is a misnomer since it is not a force nor is anything moving. It is perhaps better to call it simply MMF. In analogy to the definition of EMF
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
, the magnetomotive force
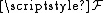 around a closed loop is defined as:
around a closed loop is defined as:
The MMF represents the potential that a hypothetical magnetic charge
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
would gain by completing the loop. The magnetic flux that is driven is not a current of magnetic charge; it merely has the same relationship to MMF that electric current has to EMF. (See microscopic origins of reluctance below for a further description.)
The unit of magnetomotive force is the ampere-turn
Ampere-turn
The ampere-turn was the MKS unit of magnetomotive force , represented by a direct current of one ampere flowing in a single-turn loop in a vacuum...
(At), represented by a steady, direct electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
of one ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
flowing in a single-turn loop of electrically conducting material in a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
. The gilbert (Gi), established by the IEC
International Electrotechnical Commission
The International Electrotechnical Commission is a non-profit, non-governmental international standards organization that prepares and publishes International Standards for all electrical, electronic and related technologies – collectively known as "electrotechnology"...
in 1930 http://www.iec.ch/about/history/, is the CGS unit of magnetomotive force and is a slightly smaller unit than the ampere-turn. The unit is named after William Gilbert (1544–1603) English physician and natural philosopher.
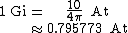
The magnetomotive force can often be quickly calculated using Ampère's law. For example, the magnetomotive force
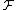 of long coil is:
of long coil is: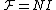 ,
,where N is the number of turns
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
and I is the current in the coil. In practice this equation is used for the MMF of real inductors with N being the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of the inducting coil.
Magnetic flux
An applied MMF 'drives' magnetic fluxMagnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through the magnetic components of the system. The magnetic flux through a magnetic component is proportional to the number of magnetic field lines that pass through the cross sectional area of that component. This is the net number, i.e. the number passing through in one direction, minus the number passing through in the other direction. The direction of the magnetic field vector B is by definition from the south to the north pole of a magnet inside the magnet; outside the field lines go from north to south.
The flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
through an element of area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the direction of magnetic field is given by the product of the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
element. More generally, magnetic flux Φ is defined by a scalar product of the magnetic field and the area element vector. Quantitatively, the magnetic flux through a surface S is defined as the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the magnetic field over the area of the surface
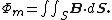
For a magnetic component the area S used to calculate the magnetic flux Φ is usually chosen to be the cross-sectional area of the component.
The SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of magnetic flux is the weber
Weber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
(in derived units: volt-seconds), and the unit of magnetic field is the weber per square meter, or tesla
Tesla (unit)
The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
.
Hopkinson's law: the magnetic analogy to Ohm's law
In electronic circuits, Ohm's lawOhm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
is an empirical relation between the EMF
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
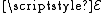 applied across an element and the current I it generates through that element. It is written as:
applied across an element and the current I it generates through that element. It is written as:
where R is the electrical resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
of that material. Hopkinson's law is a counterpart to Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
used in magnetic circuits. The law is named after the British electrical engineer, John Hopkinson
John Hopkinson
John Hopkinson, FRS, was a British physicist, electrical engineer, Fellow of the Royal Society and President of the IEE twice in 1890 and 1896. He invented the three-wire system for the distribution of electrical power, for which he was granted a patent in 1882...
. It states that
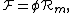
where
 is the magnetomotive force (MMF) across a magnetic element,
is the magnetomotive force (MMF) across a magnetic element, 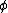 is the magnetic flux
is the magnetic fluxMagnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through the magnetic element, and
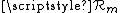 is the magnetic reluctance of that element. (It shall be shown later that this relationship is due to the empirical relationship between the H-field and the magnetic field B, B=μH, where μ is the permeability
is the magnetic reluctance of that element. (It shall be shown later that this relationship is due to the empirical relationship between the H-field and the magnetic field B, B=μH, where μ is the permeabilityPermeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of the material.) Like Ohm's law, Hopkinson's law can be interpreted either as an empirical equation that works for some materials, or it may serve as a definition of reluctance.
Reluctance
Magnetic reluctance, or magnetic resistance, is analogous to resistanceElectrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
in an electrical circuit
Electrical network
An electrical network is an interconnection of electrical elements such as resistors, inductors, capacitors, transmission lines, voltage sources, current sources and switches. An electrical circuit is a special type of network, one that has a closed loop giving a return path for the current...
(although it does not dissipate magnetic energy). In likeness to the way an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
causes an electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
to follow the path of least resistance
Path of least resistance
The path of least resistance describes the physical or metaphorical pathway that provides the least resistance to forward motion by a given object or entity, among a set of alternative paths. The concept is often used to describe why an object or entity takes a given path.In physics, the path of...
, a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
causes magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
to follow the path of least magnetic reluctance. It is a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
,
extensive quantity, akin to electrical resistance.
The total reluctance is equal to the ratio of the (MMF) in a passive magnetic circuit and the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
in this circuit. In an AC field, the reluctance is the ratio of the amplitude values for a sinusoidal MMF and magnetic flux. (see phasors)
The definition can be expressed as:

where
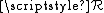 is the reluctance in ampere-turn
is the reluctance in ampere-turnAmpere-turn
The ampere-turn was the MKS unit of magnetomotive force , represented by a direct current of one ampere flowing in a single-turn loop in a vacuum...
s per weber
Weber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
(a unit that is equivalent to turns per henry).
Magnetic flux always forms a closed loop, as described by Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, but the path of the loop depends on the reluctance of the surrounding materials. It is concentrated around the path of least reluctance. Air and vacuum have high reluctance, while easily magnetized materials such as soft iron have low reluctance. The concentration of flux in low-reluctance materials forms strong temporary poles and causes mechanical forces that tend to move the materials towards regions of higher flux so it is always an attractive force(pull).
The inverse of reluctance is called permeance.

Its SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
derived unit is the henry (the same as the unit of inductance
Inductance
In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit...
, although the two concepts are distinct).
Microscopic origins of reluctance
The reluctance of a magnetically uniform magnetic circuit element can be calculated as:
where
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
s
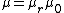 is the permeability
is the permeabilityPermeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of the material (
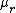 is the relative permeability of the material (dimensionless), and
is the relative permeability of the material (dimensionless), and 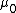 is the permeability of free space)
is the permeability of free space)
Square metre
The square metre or square meter is the SI derived unit of area, with symbol m2 . It is defined as the area of a square whose sides measure exactly one metre...
s
This is similar to the equation for electrical resistance in materials, with permeability being analogous to conductivity; the reciprocal of the permeability is known as magnetic reluctivity and is analogous to resistivity. Longer, thinner geometries with low permeabilities lead to higher reluctance. Low reluctance, like low resistance in electric circuits, is generally preferred.
Summary of analogy between magnetic circuits and electrical circuits
The following table summarizes the mathematical analogy between electrical circuit theory and magnetic circuit theory. This is mathematical analogy and not a physical one. Objects in the same row have the same mathematical role; the physics of the two theories are very different. For example, current is the flow of electrical charge, while magnetic flux is not the flow of any quantity.| Magnetic equivalent | Symbol | Units | Electric equivalent | Symbol |
|---|---|---|---|---|
| Magnetomotive force Magnetomotive force Magnetomotive force is any physical driving force that produces magnetic flux. In this context, the expression "driving force" is used in a general sense of "work potential", and is analogous, but distinct from force measured in newtons... (MMF) |
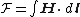 |
ampere-turn Ampere-turn The ampere-turn was the MKS unit of magnetomotive force , represented by a direct current of one ampere flowing in a single-turn loop in a vacuum... |
Definition of EMF Electromotive force In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a... |
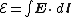 |
| Magnetic Field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
H | ampere Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... /meter |
Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... |
E |
| Magnetic Flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... |
φ | weber Weber (unit) In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :... |
Electric Current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... |
I |
| Hopkinson's Law or Rowland's Law |  |
Ohm's Law Ohm's law Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points... |
 |
|
| Reluctance |  |
1/Henry | Electrical resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical... |
R |
| Permeance | 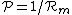 |
Henry | Electric conductance | G = 1/R |
| relation between B and H | 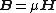 |
Microscopic Ohm's Law | 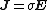 |
|
| Magnetic Flux Density B | B | tesla Tesla (unit) The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla... |
Current density Current density Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved... |
J |
| permeability Permeability (electromagnetism) In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically... |
μ | Henry/meter | Electrical conductivity | σ |
Limitations of the analogy
When using the analogy between magnetic circuits and electric circuits, the limitations of this analogy must be kept in mind. Electric and magnetic circuits are only superficially similar because of the similarity between Hopkinson's law and Ohm's law. Magnetic circuits have significant differences, which must be taken into account in their construction:- Electric currents represent the flow of particles (electrons) and carry powerPower (physics)In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
, which is dissipated as heat in resistances. Magnetic fields don't represent the "flow" of anything, and no power is dissipated in reluctances. - The current in typical electric circuits is confined to the circuit, with very little "leakage". In typical magnetic circuits not all of the magnetic field is confined to the magnetic circuit; there is significant "leakage flux" in the space outside the magnetic cores, which must be taken into account but is difficult to calculate.
- Most importantly, magnetic circuits are nonlinear; the reluctance in a magnetic circuit is not constant, as resistance is, but varies depending on the magnetic field. At high magnetic fluxes the ferromagnetic materials used for the cores of magnetic circuits saturateSaturation (magnetic)Seen in some magnetic materials, saturation is the state reached when an increase in applied external magnetizing field H cannot increase the magnetization of the material further, so the total magnetic field B levels off...
, limiting the magnetic flux, so above this level the reluctance increases rapidly. The reluctance also increases at low fluxes. In addition, ferromagnetic materials suffer from hysteresisHysteresisHysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
so the flux in them depends not just on the instantaneous MMF but also on the past history of MMF. After the source of the magnetic flux is turned off, remanent magnetism is left in ferromagnetic circuits, creating a flux with no MMF.
Circuit Laws
Magnetic circuits obey other laws that are similar to electrical circuit laws. For example, the total reluctance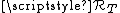 of reluctances
of reluctances 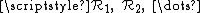 in series is:
in series is: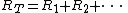
This also follows from Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
and is analogous to Kirchhoff's voltage law
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
for adding resistances in series. Also, the sum of magnetic fluxes
 into any node is always zero:
into any node is always zero: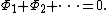
This follows from Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and is analogous to Kirchhoff's current law
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
for analyzing electrical circuits.
Together, the three laws above form a complete system for analysing magnetic circuits, in a manner similar to electric circuits. Comparing the two types of circuits shows that:
- The equivalent to resistance R is the reluctance Rm
- The equivalent to current I is the magnetic flux Φ
- The equivalent to voltage V is the magnetomotive Force F
Magnetic circuits can be solved for the flux in each branch by application of the magnetic equivalent of Kirchhoff's Voltage Law
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
(KVL) for pure source/resistance circuits. Specifically, whereas KVL states that the voltage excitation applied to a loop is equal to the sum of the voltage drops (resistance times current) around the loop, the magnetic analogue states that the magnetomotive force (achieved from ampere-turn excitation) is equal to the sum of MMF drops (product of flux and reluctance) across the rest of the loop. (If there are multiple loops, the current in each branch can be solved through a matrix equation—much as a matrix solution for mesh circuit branch currents is obtained in loop analysis—after which the individual branch currents are obtained by adding and/or subtracting the constituent loop currents as indicated by the adopted sign convention and loop orientations.) Per Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
, the excitation is the product of the current and the number of complete loops made and is measured in ampere-turns. Stated more generally:
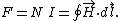
(Note that, per Stokes's theorem, the closed line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
of H dot dl around a contour is equal to the open surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
of curl H dot dA across the surface bounded by the closed contour. Since, from Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, curl H = J, the closed line integral of H dot dl evaluates to the total current passing through the surface. This is equal to the excitation, NI, which also measures current passing through the surface, thereby verifying that the net current flow through a surface is zero ampere-turns in a closed system that conserves energy.)
More complex magnetic systems, where the flux is not confined to a simple loop, must be analysed from first principles by using Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
History
The term reluctance was coined in May 1888 by Oliver HeavisideOliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
. The notion of “magnetic resistance” was first mentioned by James Joule and the term "magnetomotive force
Magnetomotive force
Magnetomotive force is any physical driving force that produces magnetic flux. In this context, the expression "driving force" is used in a general sense of "work potential", and is analogous, but distinct from force measured in newtons...
” (MMF) was first named by Bosanquet. The idea for a magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
law, similar to Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
for closed electric circuits, is attributed to H. Rowland
Henry Augustus Rowland
Henry Augustus Rowland was a U.S. physicist. Between 1899 and 1901 he served as the first president of the American Physical Society...
.
Applications
- Air gaps can be created in the cores of certain transformers to reduce the effects of saturationSaturation (magnetic)Seen in some magnetic materials, saturation is the state reached when an increase in applied external magnetizing field H cannot increase the magnetization of the material further, so the total magnetic field B levels off...
. This increases the reluctance of the magnetic circuit, and enables it to store more energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
before core saturation. This effect is also used in the flyback transformerFlyback transformerA flyback transformer , also called a line output transformer , is a special transformer, which is used for conversion of energy in electronic circuits. It was initially designed to generate high current sawtooth signals at a relatively high frequency...
.
- Variation of reluctance is the principle behind the reluctance motorReluctance motorA reluctance motor is a type of electric motor that induces non-permanent magnetic poles on the ferromagnetic rotor. Torque is generated through the phenomenon of magnetic reluctance.A reluctance motor, in its various incarnations, may be known as a:...
(or the variable reluctance generator) and the Alexanderson alternatorAlexanderson alternatorAn Alexanderson alternator is a rotating machine invented by Ernst Alexanderson in 1904 for the generation of high frequency alternating current up to 100 kHz, for use as a radio transmitter...
.
- MultimediaMultimediaMultimedia is media and content that uses a combination of different content forms. The term can be used as a noun or as an adjective describing a medium as having multiple content forms. The term is used in contrast to media which use only rudimentary computer display such as text-only, or...
loudspeakerLoudspeakerA loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
s are typically shielded magnetically, in order to reduce magnetic interference caused to televisionTelevisionTelevision is a telecommunication medium for transmitting and receiving moving images that can be monochrome or colored, with accompanying sound...
s and other CRTCathode ray tubeThe cathode ray tube is a vacuum tube containing an electron gun and a fluorescent screen used to view images. It has a means to accelerate and deflect the electron beam onto the fluorescent screen to create the images. The image may represent electrical waveforms , pictures , radar targets and...
s. The speaker magnet is covered with a material such as soft iron to minimize the stray magnetic field.
Reluctance can also be applied to:
- Reluctance motorsElectric motorAn electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
- Variable reluctance (magnetic) pickups
External links
- Magnetic-Electric Analogs by Dennis L. Feucht, Innovatia Laboratories (PDF)
- Interactive Java Tutorial on Magnetic Shunts National High Magnetic Field Laboratory
See also
- Magnetic coreMagnetic coreA magnetic core is a piece of magnetic material with a high permeability used to confine and guide magnetic fields in electrical, electromechanical and magnetic devices such as electromagnets, transformers, electric motors, inductors and magnetic assemblies. It is made of ferromagnetic metal such...
- TokamakTokamakA tokamak is a device using a magnetic field to confine a plasma in the shape of a torus . Achieving a stable plasma equilibrium requires magnetic field lines that move around the torus in a helical shape...
- Magnetic capacitivity
- Magnetic capacitanceMagnetic capacitanceMagnetic capacitance is a magnetic "reactance" which prevents magnetic "current" in oscillating magnetic circuits from rising...
- Magnetic complex reluctanceMagnetic complex reluctanceMagnetic complex reluctance is a measurement of a passive magnetic circuit dependent on sinusoidal magnetomotive force and sinusoidal magnetic flux , and this is determined by deriving the ratio of their complex effective amplitudes.[Ref...
- Reluctance motorReluctance motorA reluctance motor is a type of electric motor that induces non-permanent magnetic poles on the ferromagnetic rotor. Torque is generated through the phenomenon of magnetic reluctance.A reluctance motor, in its various incarnations, may be known as a:...

