See Leibniz (disambiguation)

Leibniz (disambiguation)

Gottfried Leibniz was a German philosopher and mathematician.In mathematics, several results and concepts are attributed to Leibniz:* Leibniz algebra, an algebraic structure...

 for other formulas known under the same name.

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Leibniz formula for

Pi

' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

, named after Gottfried Leibniz

Gottfried Leibniz

Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....

, states that


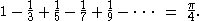
Using summation

Summation

Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...

 notation:

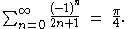
Names

The infinite series above is called the Leibniz series. It is also called the Gregory–Leibniz series

Gregory's series

Gregory's series, also known as the Madhava-Gregory series or Leibniz's series, is a mathematical series that was discovered by the Indian mathematician Madhava of Sangamagrama...

, recognizing the work of James Gregory. The formula was discovered by Madhava of Sangamagrama

Madhava of Sangamagrama

Mādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...

 and so is also called the Madhava–Leibniz series

Madhava series

In mathematics, a Madhava series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by Sangamagrama Madhava the founder of the Kerala school of astronomy and mathematics...

.

Proof

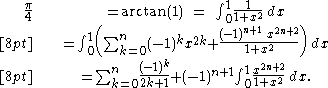
Considering only the integral in the last line, we have:


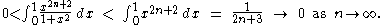
Therefore, as we are left with the Leibniz series:

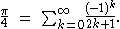
Inefficiency

Leibniz's formula converges slowly. Calculating to 10 correct decimal places using direct summation of the series requires about 5,000,000,000 terms because for .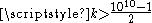

However, the Leibniz formula can be used to calculate to high precision (hundreds of digits or more) using various convergence acceleration techniques. For example, the Shanks transformation

Shanks transformation

In numerical analysis, the Shanks transformation is a non-linear series acceleration method to increase the rate of convergence of a sequence. This method is named after Daniel Shanks, who rediscovered this sequence transformation in 1955. It was first derived and published by R...

, Euler transform or Van Wijngaarden transformation, which are general methods for alternating series, can be applied effectively to the partial sums of the Leibniz series. Further, combining terms pairwise gives the non-alternating series


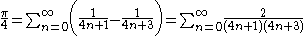
which can be evaluated to high precision from a small number of terms using Richardson extrapolation

Richardson extrapolation

In numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....

 or the Euler–Maclaurin formula. This series can also be transformed into an integral by means of the Abel–Plana formula and evaluated using techniques for numerical integration

Numerical integration

In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...

.

Unusual behavior

If the series is truncated at the right time, the decimal expansion of the approximation will agree with that of for many more digits, except for isolated digits or digit groups. For example, taking 5,000,000 terms yields

3.1415924535897932384646433832795027841971693993873058...

where the underlined digits are wrong. The errors can in fact be predicted; they are generated by the Euler numbers according to the asymptotic

Asymptotic expansion

In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...

 formula


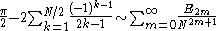
where is an integer divisible by 4. If is chosen to be a power of ten, each term in the right sum becomes a finite decimal fraction. The formula is a special case of the Boole summation formula for alternating series, providing yet another example of a convergence acceleration technique that can be applied to the Leibniz series. In 1992, Jonathan Borwein

Jonathan Borwein

Jonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...

 and Mark Limber used the first thousand Euler numbers to calculate to 5,263 decimal places with Leibniz' formula.

External links

• Leibniz Formula in C, x86 FPU Assembly, x86-64 SSE3 Assembly, and DEC Alpha Assembly