Surya Siddhanta
Encyclopedia
The Surya Siddhanta is one of the earliest siddhanta
in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta
is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras were enemies of the Deva, the Gods of Hindus. Asuras were believed to residents of the nether worlds.
Significant coverage is on kinds of time, length of the year of gods and demons, day and night of god Brahma, the elapsed period since creation, how planets move eastwards and sidereal revolution. The lengths of the Earth's diameter, circumference are also given. Eclipses and color of the eclipsed portion of the moon is mentioned. This explains the archeo-astronomical basis for the sequence of days of the week named after the Sun, Moon, etc. Musings that there is no above and below and that movement of the starry sphere is left to right for Asuras makes interesting reading.
Varahamihira
in his Panchasiddhantika contrasts it with four other treatises, besides the Paitamaha Siddhantas (which is more similar to the "classical" Vedanga Jyotisha
), the Paulisha and Romaka
Siddhantas (directly based on Hellenistic astronomy) and the Vasishta Siddhanta. Citation of the Surya Siddhanta is also found in the works of Aryabhata
.
The work referred to by the title Surya Siddhanta has been repeatedly recast. There may have been an early work under that title dating back to the Buddhist Age of India (3rd century BC). The work as preserved and edited by Burgess (1860) dates to the Middle Ages. Utpala
, a 10th century commentator of Varahamihira, quotes six shlokas of the Surya Siddhanta of his day, not one of which is to be found in the text now known as the Surya Siddhanta. The present Surya Siddhanta may nevertheless be considered a direct descendant of the text available to Varahamihira. This article discusses the text as edited by Burgess. For what evidence we have of the Gupta period text, see Pancha-Siddhantika. It has rules laid down to determine the true motions of the luminaries, which conform to their actual positions in the sky. It gives the locations of several stars other than the lunar nakshatra
s and treats the calculation of solar eclipse
s. as well as solstices eg.summer solstice 21/06
Methods for accurately calculating the shadow cast by a gnomon
are discussed in both Chapters 3 and 13.
When computed, this astronomical time cycle would give the following results:
The actual astronomical value stated for the sidereal year however, is not as accurate. The length of the sidereal year is stated to be 365.258756 days, which is longer than the modern value by 3 minutes 27 seconds. This is due to the text using a different method for actual astronomical computation, rather than the Hindu cosmological time cycles copied from an earlier text, probably because the author didn't understand how to compute the complex time cycles. The author instead employed a mean motion
for the Sun and a constant of precession
inferior to that used in the Hindu cosmological time cycles.
s. The estimate for the diameter of Mercury
is 3,008 miles, an error of less than 1% from the currently accepted diameter of 3,032 miles. It also estimates the diameter of Saturn
as 73,882 miles, which again has an error of less than 1% from the currently accepted diameter of 74,580. Its estimate for the diameter of Mars
is 3,772 miles, which has an error within 11% of the currently accepted diameter of 4,218 miles. It also estimated the diameter of Venus
as 4,011 miles and Jupiter
as 41,624 miles, which are roughly half the currently accepted values, 7,523 miles and 88,748 miles, respectively.
. It uses sine
(jya), cosine (kojya or "perpendicular sine") and inverse sine (otkram jya) for the first time, and also contains the earliest use of the tangent and secant
when discussing the shadow cast by a gnomon
in verses 21–22 of Chapter 3:
In modern notation, this gives the shadow of the gnomon
at mid-day as
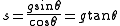
and the hypotenuse of the gnomon at mid-day as
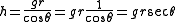
where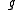
is the measure of the gnomon, 
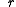is the radius of the gnomon, 
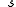is the shadow of the gnomon, and 
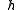is the hypotenuse of the gnomon.
and lunisolar calendar
s are widely used, with their local variations, in different parts of India. They are important in predicting the dates for the celebration of various festivals, performance of various rites as well as on all astronomical matters. The modern Indian solar and lunisolar calendars are based on close approximations to the true times of the Sun’s entrance into the various rasis.
Conservative "panchang" (almanac
) makers still use the formulae and equations found in the Surya Siddhanta to compile and compute their panchangs. The panchang is an annual publication published in all regions and languages in India containing all calendrical information on religious, cultural and astronomical events. It exerts great influence on the religious and social life of the people in India and is found in most Hindu households.
Siddhanta
Siddhanta, a Sanskrit term, roughly translates as the Doctrine or the Tradition. It denotes the established and accepted view of a particular school within Indian philosophy.-Hindu philosophy:...
in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta
Siddhanta
Siddhanta, a Sanskrit term, roughly translates as the Doctrine or the Tradition. It denotes the established and accepted view of a particular school within Indian philosophy.-Hindu philosophy:...
is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras were enemies of the Deva, the Gods of Hindus. Asuras were believed to residents of the nether worlds.
Significant coverage is on kinds of time, length of the year of gods and demons, day and night of god Brahma, the elapsed period since creation, how planets move eastwards and sidereal revolution. The lengths of the Earth's diameter, circumference are also given. Eclipses and color of the eclipsed portion of the moon is mentioned. This explains the archeo-astronomical basis for the sequence of days of the week named after the Sun, Moon, etc. Musings that there is no above and below and that movement of the starry sphere is left to right for Asuras makes interesting reading.
Varahamihira
Varahamihira
Varāhamihira , also called Varaha or Mihira, was an Indian astronomer, mathematician, and astrologer who lived in Ujjain...
in his Panchasiddhantika contrasts it with four other treatises, besides the Paitamaha Siddhantas (which is more similar to the "classical" Vedanga Jyotisha
Vedanga Jyotisha
The ' is an Indian text on Jyotisha, redacted by Lagadha .The text is foundational to the Vedanga discipline of Jyotisha. It is dated to the final centuries BCE...
), the Paulisha and Romaka
Romaka Siddhanta
The Romaka Siddhanta is an Indian astronomical treatise, based on the astronomical learning of Byzantine Rome...
Siddhantas (directly based on Hellenistic astronomy) and the Vasishta Siddhanta. Citation of the Surya Siddhanta is also found in the works of Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
.
The work referred to by the title Surya Siddhanta has been repeatedly recast. There may have been an early work under that title dating back to the Buddhist Age of India (3rd century BC). The work as preserved and edited by Burgess (1860) dates to the Middle Ages. Utpala
Utpala
Utpala or ' is the name of a 10th century Indian commentator of Vārāha Mihira's Brihat Samhitā. Brihat Samhitā is a Samhitā text of . Samhitā is one of three branches of Utpala or ' is the name of a 10th century Indian commentator of Vārāha Mihira's Brihat Samhitā. Brihat Samhitā is a...
, a 10th century commentator of Varahamihira, quotes six shlokas of the Surya Siddhanta of his day, not one of which is to be found in the text now known as the Surya Siddhanta. The present Surya Siddhanta may nevertheless be considered a direct descendant of the text available to Varahamihira. This article discusses the text as edited by Burgess. For what evidence we have of the Gupta period text, see Pancha-Siddhantika. It has rules laid down to determine the true motions of the luminaries, which conform to their actual positions in the sky. It gives the locations of several stars other than the lunar nakshatra
Nakshatra
Nakshatra is the term for lunar mansion in Hindu astrology. A nakshatra is one of 27 sectors along the ecliptic...
s and treats the calculation of solar eclipse
Solar eclipse
As seen from the Earth, a solar eclipse occurs when the Moon passes between the Sun and the Earth, and the Moon fully or partially blocks the Sun as viewed from a location on Earth. This can happen only during a new moon, when the Sun and the Moon are in conjunction as seen from Earth. At least...
s. as well as solstices eg.summer solstice 21/06
Astronomy
The table of contents in this text are:- The Motions of the PlanetPlanetA planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s - The Places of the Planets
- Direction, Place and Time
- The MoonMoonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and EclipseEclipseAn eclipse is an astronomical event that occurs when an astronomical object is temporarily obscured, either by passing into the shadow of another body or by having another body pass between it and the viewer...
s - The SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and Eclipses - The Projection of Eclipses
- Planetary Conjunctions
- Of the StarStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s - RisingRisingRising may refer to:In art and media:* Rising , the last novel of R. C. Hutchinson* The following albums:** Rising ** Rising ** Rising ** Rising...
s and Settings - The Moon's Risings and Settings
- Certain Malignant Aspects of the Sun and Moon
- Cosmogony, Geography, and Dimensions of the Creation
- The GnomonGnomonThe gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
- The Movement of the Heavens and Human Activity
Methods for accurately calculating the shadow cast by a gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
are discussed in both Chapters 3 and 13.
Time cycles
The astronomical time cycles contained in the text were remarkably accurate at the time. The Hindu Time Cycles, copied from an earlier work, are described in verses 11–23 of Chapter 1:- 11. That which begins with respirations (prana) is called real.... Six respirations make a vinadi, sixty of these a nadi;
- 12. And sixty nadis make a sidereal day and night. Of thirty of these sidereal days is composed a month; a civil (savana) month consists of as many sunrises;
- 13. A lunar month, of as many lunar days (tithi); a solar (saura) month is determined by the entrance of the sun into a sign of the zodiac; twelve months make a year. This is called a day of the gods.
- 14. The day and night of the gods and of the demons are mutually opposed to one another. Six times sixty of them are a year of the gods, and likewise of the demons.
- 15. Twelve thousand of these divine years are denominated a caturyuga; of ten thousand times four hundred and thirty-two solar years
- 16. Is composed that caturyuga, with its dawn and twilight. The difference of the krtayuga and the other yugas, as measured by the difference in the number of the feet of Virtue in each, is as follows:
- 17. The tenth part of a caturyuga, multiplied successively by four, three, two, and one, gives the length of the krta and the other yugas: the sixth part of each belongs to its dawn and twilight.
- 18. One and seventy caturyugas make a manu; at its end is a twilight which has the number of years of a krtayuga, and which is a deluge.
- 19. In a kalpa are reckoned fourteen manus with their respective twilights; at the commencement of the kalpa is a fifteenth dawn, having the length of a krtayuga.
- 20. The kalpa, thus composed of a thousand caturyugas, and which brings about the destruction of all that exists, is a day of Brahma; his night is of the same length.
- 21. His extreme age is a hundred, according to this valuation of a day and a night. The half of his life is past; of the remainder, this is the first kalpa.
- 22. And of this kalpa, six manus are past, with their respective twilights; and of the Manu son of Vivasvant, twenty-seven caturyugas are past;
- 23. Of the present, the twenty-eighth, caturyuga, this krtayuga is past....
When computed, this astronomical time cycle would give the following results:
- The average length of the tropical yearTropical yearA tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
as 365.2421756 days, which is only 1.4 seconds shorter than the modern value of 365.2421904 days (J2000).
- The average length of the sidereal yearSidereal yearA sidereal year is the time taken by the Earth to orbit the Sun once with respect to the fixed stars. Hence it is also the time taken for the Sun to return to the same position with respect to the fixed stars after apparently travelling once around the ecliptic. It was equal to at noon 1 January...
, the actual length of the Earth's revolution around the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, as 365.2563627 days, which is virtually the same as the modern value of 365.25636305 days (J2000). This remained the most accurate estimate for the length of the sidereal year anywhere in the world for over a thousand years.
The actual astronomical value stated for the sidereal year however, is not as accurate. The length of the sidereal year is stated to be 365.258756 days, which is longer than the modern value by 3 minutes 27 seconds. This is due to the text using a different method for actual astronomical computation, rather than the Hindu cosmological time cycles copied from an earlier text, probably because the author didn't understand how to compute the complex time cycles. The author instead employed a mean motion
Mean motion
Mean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
for the Sun and a constant of precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
inferior to that used in the Hindu cosmological time cycles.
Planetary diameters
The Surya Siddhanta also estimates the diameters of the planetPlanet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s. The estimate for the diameter of Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
is 3,008 miles, an error of less than 1% from the currently accepted diameter of 3,032 miles. It also estimates the diameter of Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
as 73,882 miles, which again has an error of less than 1% from the currently accepted diameter of 74,580. Its estimate for the diameter of Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
is 3,772 miles, which has an error within 11% of the currently accepted diameter of 4,218 miles. It also estimated the diameter of Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
as 4,011 miles and Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
as 41,624 miles, which are roughly half the currently accepted values, 7,523 miles and 88,748 miles, respectively.
Trigonometry
The Surya Siddhanta contains the roots of modern trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
. It uses sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
(jya), cosine (kojya or "perpendicular sine") and inverse sine (otkram jya) for the first time, and also contains the earliest use of the tangent and secant
Secant
Secant is a term in mathematics. It comes from the Latin secare . It can refer to:* a secant line, in geometry* the secant variety, in algebraic geometry...
when discussing the shadow cast by a gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
in verses 21–22 of Chapter 3:
Of [the sun's meridian zenith distance] find the jya ("base sine") and kojya (cosine or "perpendicular sine"). If then the jya and radius be multiplied respectively by the measure of the gnomon in digits, and divided by the kojya, the results are the shadow and hypotenuseHypotenuseIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
at mid-day.
In modern notation, this gives the shadow of the gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
at mid-day as
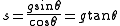
and the hypotenuse of the gnomon at mid-day as
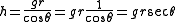
where
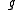is the measure of the gnomon, 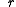is the radius of the gnomon, 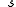is the shadow of the gnomon, and 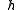is the hypotenuse of the gnomon.Calendrical uses
The Indian solarSolar calendar
A solar calendar is a calendar whose dates indicate the position of the earth on its revolution around the sun .-Tropical solar calendars:...
and lunisolar calendar
Lunisolar calendar
A lunisolar calendar is a calendar in many cultures whose date indicates both the moon phase and the time of the solar year. If the solar year is defined as a tropical year then a lunisolar calendar will give an indication of the season; if it is taken as a sidereal year then the calendar will...
s are widely used, with their local variations, in different parts of India. They are important in predicting the dates for the celebration of various festivals, performance of various rites as well as on all astronomical matters. The modern Indian solar and lunisolar calendars are based on close approximations to the true times of the Sun’s entrance into the various rasis.
Conservative "panchang" (almanac
Almanac
An almanac is an annual publication that includes information such as weather forecasts, farmers' planting dates, and tide tables, containing tabular information in a particular field or fields often arranged according to the calendar etc...
) makers still use the formulae and equations found in the Surya Siddhanta to compile and compute their panchangs. The panchang is an annual publication published in all regions and languages in India containing all calendrical information on religious, cultural and astronomical events. It exerts great influence on the religious and social life of the people in India and is found in most Hindu households.
Editions
- Translation of the Sûrya-Siddhânta: A text-book of Hindu astronomy, with notes and an appendix by Ebenezer Burgess Originally published: Journal of the American Oriental Society 6 (1860) 141–498. Commentary by Burgess is much larger than his translation.
- Surya-Siddhanta: A Text Book of Hindu Astronomy by Ebenezer Burgess, ed. Phanindralal Gangooly (1989/1997) with a 45-page commentary by P. C. Sengupta (1935).
- Translation of the Surya Siddhanta by Bapu Deva Sastri (1861) ISBN 3764813342, ISBN 9783764813345. Only a few notes. Translation of Surya Siddhanta occupies first 100 pages; rest is a translation of the Siddhanta Siromani by Lancelot Wilkinson.
- Surya Siddhanta Sanskrit text in Devanagari.
- सूर्यसिद्धान्त (in Unicode Devanagari)
Further reading
- Victor J. Katz. A History of Mathematics: An Introduction, 1998.
- Dwight William Johnson. Exegesis of Hindu Cosmological Time Cycles, 2003.