Lunar theory
Encyclopedia
Lunar theory attempts to account for the motions of the Moon
. There are many irregularities (or perturbation
s) in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays (see Modern developments) modelled to a very high degree of accuracy. Several aspects of lunar theory have accordingly become largely about history. But newly achieved levels of accuracy have also turned lunar theory into a sensitive instrument for new tests of physical theories.
Lunar theory includes:
Lunar theory has a history of over 2000 years of investigation. Its more modern developments have been used over the last three centuries for fundamental scientific and technological purposes, and are still being used in that way.
Among notable astronomers and mathematicians down the ages, whose names are associated with lunar theories, are --
and other notable mathematical astronomers also made significant contributions, including: Edmond Halley
; comte de Pontécoulant; J C Adams
; G W Hill
; and Simon Newcomb
.
The history can be considered to fall into three parts: from ancient times to Newton; the period of classical (Newtonian) physics; and modern developments.
had made bare mention of three astronomical schools in Mesopotamia
– at Babylon, Uruk and 'Hipparenum' (possibly 'Sippar'). But definite modern knowledge of any details only began when J Epping
deciphered cuneiform texts on clay tablets from a Babylonian archive: in these texts he identified an ephemeris of positions of the Moon. Since then, knowledge of the subject, still fragmentary, has had to be built up by painstaking analysis of deciphered texts, mainly in numerical form, on tablets from Babylon and Uruk (no trace has yet been found of anything from the third school mentioned by Pliny).
To the Babylon
ian astronomer Kidinnu
(in Greek or Latin, Kidenas or Cidenas) has been attributed the invention (5th or 4th century BC) of a system "B" for predicting the position of the moon, taking account that the moon continually changes its speed along its path relative to the background of fixed stars. This system involved calculating daily stepwise changes of lunar speed, up or down, with a minimum and a maximum approximately each month. The basis of these systems appears to have been arithmetical rather than geometrical, but they did approximately account for the main lunar inequality now known as the equation of the center
.
The Babylonians appear to have been interested in calendars, new moons and eclipses. Some time between the years 500 BC and 400 BC they identified and began to use the 19-year cyclic relation between lunar months and solar years now known as the Metonic cycle
.
They built up a numerical theory of the main irregularities in the Moon's motion, reaching remarkably good estimates for the (different) periods of the three most prominent features of the Moon's motion:-
The Babylonian estimate for the synodic month was adopted for the greater part of two millennia by Hipparchus, Ptolemy and medieval writers (and it is still in use as part of the basis for the calculated Hebrew (Jewish) calendar).
and Ptolemy
down to the time of Newton
's work in the seventeenth century, lunar theories were composed mainly with the help of geometrical ideas, inspired more or less directly by long series of positional observations of the moon. Prominent in these geometrical lunar theories were combinations of circular motions – applications of the theory of epicycles. It wasn't until the work of Ibn al-Shatir
in the 14th century that the need for epicycles in lunar theory was eliminated.
, whose works are mostly lost and known mainly from quotations by other authors, assumed that the Moon moved in a circle inclined at 5° to the ecliptic
, rotating in a retrograde direction (i.e. opposite to the direction of annual and monthly apparent movements of the Sun and Moon relative to the fixed stars) once in 18 2/3 years. The circle acted as a deferent, carrying an epicycle along which the Moon was assumed to move in a retrograde direction. The center of the epicycle moved at a rate corresponding to the mean change in Moon's longitude, while the period of the Moon around the epicycle was an anomalistic month. This epicycle approximately provided for what was later recognized as the elliptical inequality, the equation of the center
, and its size approximated to an equation of the center of about 5° 1'. This figure is much smaller than the modern value: but it is close to the difference between the modern coefficients of the equation of the center (1st term) and that of the evection: the difference is accounted for by the fact that the ancient measurements were taken at times of eclipses, and the effect of the evection (which subtracts under those conditions from the equation of the center) was at that time unknown and overlooked. For further information see also separate article Evection
.
's work the 'Almagest
' had wide and long-lasting acceptance and influence for over a millennium. He gave a geometrical lunar theory that improved on that of Hipparchus by providing for a second inequality of the Moon's motion, using a device that made the apparent apogee oscillate a little – 'prosneusis' of the epicycle. This 'second inequality' or 'second anomaly' accounted rather approximately, not only for the equation of the center, but also for what became known (much later) as the evection. But this theory, applied to its logical conclusion, would make the distance (and apparent diameter) of the Moon appear to vary by a factor of about 2, which is clearly not seen in reality. (The apparent angular diameter of the Moon does vary monthly, but only over a much narrower range of about 0.49-0.55°.) This defect of the Ptolemaic theory was part of what led to its eventual replacement in the 17th century.
was made by the Arab astronomer, Ibn al-Shatir
(1304–1375), in the 14th century. Building on previous work carried out at the Maragheh observatory
in the previous century as well as his own observations and experimental tests at the Umayyad Mosque
, he produced the first model of lunar motion that matched physical observations, and eliminated the need for any eccentric, epicycle
or equant
mechanisms that previous lunar models depended upon. This development in lunar theory was later employed by the Renaissance
astronomer Nicolaus Copernicus
, who used an identical lunar model to that of Ibn al-Shatir.
and Kepler refined the Ptolemaic lunar theory, but did not overcome its central defect of giving a poor account of the (mainly monthly) variations in the Moon's distance, apparent diameter and parallax. Their work added to the lunar theory three substantial further discoveries. (1) The nodes and the inclination of the lunar orbital plane both appear to librate, with a monthly (according to Tycho) or semi-annual period (according to Kepler). (2) The lunar longitude has a twice-monthly 'Variation', by which the Moon moves faster than expected at new and full moon, and slower than expected at the quarters. (3) There is also an annual effect, by which the lunar motion slows down a little in January and speeds up a little in July: the 'annual equation'.
The refinements of Tycho and Kepler were recognized by their immediate successors as improvements, but their seventeenth-century successors tried numerous alternative geometrical configurations for the lunar motions in order to improve matters further. A notable success was achieved by Jeremiah Horrocks
, who proposed a scheme involving an approximate 6-monthly libration in the position of the lunar apogee and also in the size of the elliptical eccentricity. This scheme had the great merit of giving a more realistic description of the changes in distance, diameter and parallax of the Moon.
. He was the first to define the problem of the perturbed motion of the Moon in recognisably modern terms. His groundbreaking work is shown for example in the 'Principia' in all versions including the first edition published in 1687.
Thus Newton concluded that it is only the difference between the Sun's accelerative attraction on the Moon and the Sun's attraction on the Earth that perturbs the motion of the Moon relative to the Earth.
Newton then in effect used vector decomposition
of forces, to carry out this analysis. In Book 1, Proposition 66 and in Book 3, Proposition 25, he showed by a geometrical construction, starting from the total gravitational attraction of the Sun on the Earth, and of the Sun on the Moon, the difference that represents the perturbing effect on the motion of the Moon relative to the Earth. In summary, line LS in Newton's diagram as shown below represents the size and direction of the perturbing acceleration acting on the Moon in the Moon's current position P (line LS does not pass through point P, but the text shows that this is not intended to be significant, it is a result of the scale factors and the way the diagram has been built up).
Shown here is Newton's diagram from the first (1687) Latin edition of the Principia (Book 3, Proposition 25, at p. 434). Here he introduced his analysis of perturbing accelerations on the Moon in the Sun-Earth-Moon system. Q represents the Sun, S the Earth, and P the Moon.
Parts of this diagram represent distances, other parts gravitational accelerations (attractive forces per unit mass). In a dual significance, SQ represents the Earth-Sun distance, and then it also represents the size and direction of the Earth-Sun gravitational acceleration. Other distances in the diagram are then in proportion to distance SQ. Other attractions are in proportion to attraction SQ.
The Sun's attractions are SQ (on the Earth) and LQ (on the Moon). The size of LQ is drawn so that the ratio of attractions LQ:SQ is the inverse square of the ratio of distances PQ:SQ. (Newton constructs KQ=SQ, giving an easier view of the proportions.) The Earth's attraction on the Moon acts along direction PS. (But line PS signifies only distance and direction so far, nothing has been defined about the scale factor between solar and terrestrial attractions).
After showing solar attractions LQ on the Moon and SQ on the Earth, on the same scale, Newton then makes a vector decomposition of LQ into components LM and MQ. Then he identifies the perturbing acceleration on the Moon as the difference of this from SQ. SQ and MQ are parallel to each other, so SQ can be directly subtracted from MQ, leaving MS. The resulting difference, after subtracting SQ from LQ, is therefore the vector sum of LM and MS: these add up to a perturbing acceleration LS.
Later Newton identified another resolution of the perturbing acceleration LM+MS = LS, into orthogonal components: a transverse component parallel to LE, and a radial component, effectively ES.
Newton's diagrammatic scheme, since his time, has been re-presented in other and perhaps visually clearer ways. Shown here is a vector presentation indicating, for two different positions, P1 and P2, of the Moon in its orbit around the Earth, the respective vectors LS1 and LS2 for the perturbing acceleration due to the Sun. The Moon's position at P1 is fairly close to what it was at P in Newton's diagram; corresponding perturbation LS1 is like Newton's LS in size and direction. At another position P2, the Moon is farther away from the Sun than the Earth is, the Sun's attraction LQ2 on the Moon is weaker than the Sun's attraction SQ=SQ2 on the Earth, and then the resulting perturbation LS2 points obliquely away from the Sun.
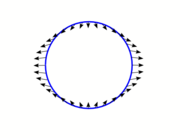Constructions like those in Newton's diagram can be repeated for many different positions of the Moon in its orbit. For each position, the result is a perturbation vector like LS1 or LS2 in the second diagram. Shown here is an often-presented form of the diagram that summarises sizes and directions of the perturbation vectors for many different positions of the Moon in its orbit. Each small arrow is a perturbation vector like LS, applicable to the Moon in the particular position around the orbit from which the arrow begins. The perturbations on the Moon when it is nearly in line along the Earth-Sun axis, i.e. near new or full moon, point outwards, away from the Earth. When the Moon-Earth line is 90° from the Earth-Sun axis they point inwards, towards the Earth, with a size that is only half the maximum size of the axial (outwards) perturbations. (Newton gave a rather good quantitative estimate for the size of the solar perturbing force: at quadrature
where it adds to the Earth's attraction he put it at 1/178.725 of the mean terrestrial attraction, and twice as much as that at the new and full moons where it opposes and diminishes the Earth's attraction.)
Newton also showed that the same pattern of perturbation applies, not only to the Moon, in its relation to the Earth as disturbed by the Sun, but also to other particles more generally in their relation to the solid Earth as disturbed by the Sun (or by the Moon); for example different portions of the tidal waters at the Earth's surface. The study of the common pattern of these perturbing accelerations grew out of Newton's initial study of the perturbations of the Moon, which he also applied to the forces moving tidal waters. Nowadays this common pattern itself has become often known as a tidal force
whether it is being applied to the disturbances of the motions of the Moon, or of the Earth's tidal waters – or of the motions of any other object that suffers perturbations of analogous pattern.
After introducing his diagram 'to find the force of the Sun to perturb the Moon' in Book 3, Proposition 25, Newton developed a first approximation to the solar perturbing force, showing in further detail how its components vary as the Moon follows its monthly path around the Earth. He also took the first steps in investigating how the perturbing force shows its effects by producing irregularities in the lunar motions. (In this part of the enterprise, Newton's success was more limited: it is relatively uncomplicated to define the perturbing forces, but heavy complexities soon arise in the problem of working out the resulting motions, and these were to challenge mathematical astronomers for two centuries after Newton's initial definition of the problem and indication of the directions to take in solving it.)
For a selected few of the lunar inequalities, Newton showed in some quantitative detail how they arise from the solar perturbing force.
Much of this lunar work of Newton's was done in the 1680s, and the extent and accuracy of his first steps in the gravitational analysis was limited by several factors, including his own choice to develop and present the work in what was, on the whole, a difficult geometrical way, and by the limited accuracy and uncertainty of many astronomical measurements in his time.
, Alexis Clairaut and Jean d'Alembert in the mid-eighteenth century, down to E W Brown
in the late nineteenth and early twentieth century, was to account completely and much more precisely for the moon's motions on the basis of Newton's laws, i.e. the laws of motion
and of universal gravitation by attractions inversely proportional to the squares of the distances between the attracting bodies. They also wished to put the inverse-square law of gravitation to the test, and for a time in the 1740s it was seriously doubted, on account of what was then thought to be a large discrepancy between the Newton-theoretical and the observed rates in the motion of the lunar apogee. However Clairaut showed shortly afterwards (1749–50) that at least the major cause of the discrepancy lay not in the lunar theory based on Newton's laws, but in excessive approximations that he and others had relied on to evaluate it.
Most of the improvements in theory after Newton were made in algebraic form: they involved voluminous and highly laborious amounts of infinitesimal calculus and trigonometry. It also remained necessary, for completing the theories of this period, to refer to observational measurements.
, Clairaut and d'Alembert, it was recognized that nearly all of the main lunar perturbations could be expressed in terms of just a few angular arguments and coefficients. These can be represented by:
From these basic parameters, just four basic differential angular arguments are enough to express, in their different combinations, nearly all of the most significant perturbations of the lunar motions. They are given here with their conventional symbols due to Delaunay
; they are sometimes known as the Delaunay arguments:
This work culminated into Brown´s
lunar theory (1897..1908) and Tables of the Motion of the Moon (1919). These were used in the American Ephemeris and Nautical Almanac
until 1968, and in a modified form until 1984.
The analysts of the mid-18th century expressed the perturbations of the Moon's position in longitude using about 25-30 trigonometrical terms. The number of terms needed to express the Moon's position with the accuracy sought at the beginning of the twentieth century was over 1400; and the number of terms needed to emulate the accuracy of modern numerical integrations based on laser-ranging observations is in the tens of thousands: there is no limit to the increase in number of terms needed as requirements of accuracy increase.
Wallace John Eckert
, a student of Brown who worked at IBM, used the experimental digital computers developed there after the second world war for computation of astronomical ephemerides. One of the projects was to put Brown's lunar theory into the machine and evaluate the expressions directly. Another project was something entirely new: a numerical integration
of the equations of motion for the Sun and the four major planets. This became feasible only after electronic digital computers became available. Eventually this led to the Jet Propulsion Laboratory Development Ephemeris series.
In the mean time, Brown's theory was improved with better constants and the introduction of Ephemeris Time
and the removal of some empirical corrections associated with this. This led to the Improved Lunar Ephemeris (ILE), which, with some minor successive improvements, was used in the astronomical almanacs from 1960 through 1983 (ILE j=0 from 1960 to 1967, ILE j=1 from 1968 to 1971, ILE j=2 from 1972 to 1983), and was used to bring men to the moon.
The most significant improvement of position observations of the moon have been the lunar laser ranging measurements, obtained using earth-bound lasers and special retro-reflectors placed on the surface of the moon. The time-of-flight of a pulse of laser light to one of the reflectors and back gives a measure of the moon's distance at that time. The first of four reflectors which are still operational today was taken to the moon in the Apollo 11
spacecraft in July 1969 and placed in suitable position on the Moon's surface by Neil Armstrong
.
The precision of this science
is currently being extended still further by the recently-established Apache Point Observatory Lunar Laser-ranging Operation
.
at California Institute of Technology
; and names particularly associated with the transition, from the early 1970s onwards, from classical lunar theories and ephemerides towards the modern state of the science include those of J Derral Mulholland and J G Williams (and for the linked development of solar system (planetary) ephemerides E Myles Standish).
Since the 1970s, the Jet Propulsion Laboratory
(JPL) has produced a series of numerically integrated Development Ephemerides (numbered DExxx), incorporating Lunar Ephemerides (LExxx). Planetary and lunar ephemerides DE200/LE200 were used in the official Astronomical Almanac ephemerides for 1984–2002, and ephemerides DE405/LE405, of further improved accuracy and precision, have been in use as from the issue for 2003.U S Naval Observatory (2009) History of the Astronomical Almanac.
by Jean Chapront and Michelle Chapront-Touzé from the Bureau des Longitudes
. Using computer-assisted algebra, the analytical developments have been taken further than previously could be done by the classical analysts working manually. Also, some of these new analytical theories (like ELP) have been fitted to the numerical ephemerides previously developed at JPL as mentioned above. The main aims of these recent analytical theories, in contrast to the aims of the classical theories of past centuries, have not been to generate improved positional data for current dates; rather, their aims have included the study of further aspects of the motion, such as long-term properties, which may not so easily be apparent from the modern numerical theories themselves.
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
. There are many irregularities (or perturbation
Perturbation (astronomy)
Perturbation is a term used in astronomy in connection with descriptions of the complex motion of a massive body which is subject to appreciable gravitational effects from more than one other massive body....
s) in the Moon's motion, and many attempts have been made over a long history to account for them. After centuries of being heavily problematic, the lunar motions are nowadays (see Modern developments) modelled to a very high degree of accuracy. Several aspects of lunar theory have accordingly become largely about history. But newly achieved levels of accuracy have also turned lunar theory into a sensitive instrument for new tests of physical theories.
Lunar theory includes:
- the background of general theory; including mathematical techniques used to analyze the Moon's motion and to generate formulae and algorithms for predicting its movements; and also
- quantitative formulae, algorithms, and geometrical diagrams that may be used to compute the Moon's position for a given time; often by the help of tables based on the algorithms.
Lunar theory has a history of over 2000 years of investigation. Its more modern developments have been used over the last three centuries for fundamental scientific and technological purposes, and are still being used in that way.
Applications of lunar theory
Applications of lunar theory have included the following:-- In the eighteenth century, comparison between lunar theory and observation was used to test Newton's law of universal gravitationNewton's law of universal gravitationNewton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
by the motion of the lunar apogee; - In the eighteenth and nineteenth centuries, navigational tables based on lunar theory, initially in the Nautical AlmanacThe Nautical AlmanacThe Nautical Almanac has been the familiar name for a series of official British almanacs published under various titles since the first issue of The Nautical Almanac and Astronomical Ephemeris, for 1767: this was the first nautical almanac ever to contain data dedicated to the convenient...
, were much used for the determination of longitude at sea by the method of lunar distances; - In the very early twentieth century, comparison between lunar theory and observation was used in another test of gravitational theory, to test (and rule out) Simon NewcombSimon NewcombSimon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
's suggestion that a well-known discrepancy in the motion of the perihelion of Mercury might be explained by a fractional adjustment of the power -2 in Newton's inverse square law of gravitation: (the discrepancy was later successfully explained by the general theory of relativity); - In the mid-twentieth century, before the development of atomic clocks, lunar theory and observation were used in combination to implement an astronomical time scale (ephemeris timeEphemeris timeThe term ephemeris time can in principle refer to time in connection with any astronomical ephemeris. In practice it has been used more specifically to refer to:...
) free of the irregularities of mean solar time; - In the late twentieth and early twenty-first centuries, modern developments of lunar theory are being used, in conjunction with high-precision observations, to test the exactness of physical relationships associated with the general theory of relativity, including the strong equivalence principle, relativistic gravitation, geodetic precession, and the constancy of the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. - position of the Moon can be used along with position of Sun, bright planets and stars for navigation of ship or aircraft, when modern methods (such as GPS) are not available.
History
The Moon has been observed for millennia. Over these ages, various levels of care and precision have been possible, according to the techniques of observation available at any time. There is a correspondingly long history of lunar theories: it stretches from the times of the Babylonian and Greek astronomers, down to modern lunar laser ranging.Among notable astronomers and mathematicians down the ages, whose names are associated with lunar theories, are --
- Babylonian/Chaldean:- NaburimannuNaburimannuNabu-ri-man-nu was a Chaldean astronomer and mathematician.Classical and ancient cuneiform sources mention an astronomer with this name:...
, KidinnuKidinnuKidinnu was a Chaldean astronomer and mathematician. Strabo of Amaseia called him Kidenas, Pliny the Elder Cidenas, and Vettius Valens Kidynas....
, Soudines - Greek/Hellenistic:- HipparchusHipparchusHipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
, PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the... - Arab:- Ibn al-ShatirIbn al-ShatirAla Al-Din Abu'l-Hasan Ali Ibn Ibrahim Ibn al-Shatir was an Arab Muslim astronomer, mathematician, engineer and inventor who worked as muwaqqit at the Umayyad Mosque in Damascus, Syria.-Astronomy:...
- European, 16th to early 20th centuries:-
- Tycho BraheTycho BraheTycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
- Johannes KeplerJohannes KeplerJohannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
- Jeremiah HorrocksJeremiah HorrocksJeremiah Horrocks , sometimes given as Jeremiah Horrox , was an English astronomer who was the only person to predict, and one of only two people to observe and record, the transit of Venus of 1639.- Life and work :Horrocks was born in Lower Lodge, in...
- BullialdusIsmaël BullialdusIsmaël Bullialdus was a French astronomer.Bullialdus was born Ismaël Boulliau in Loudun, Vienne, France, the first surviving son to Calvinists Susanna Motet and Ismaël Boulliau, a notary by profession and amateur astronomer. At age twenty-one he converted to Catholicism, and by twenty-six was...
- John FlamsteedJohn FlamsteedSir John Flamsteed FRS was an English astronomer and the first Astronomer Royal. He catalogued over 3000 stars.- Life :Flamsteed was born in Denby, Derbyshire, England, the only son of Stephen Flamsteed...
- Isaac NewtonIsaac NewtonSir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
- Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
- Alexis Clairaut
- Jean d'Alembert
- Tobias MayerTobias MayerTobias Mayer was a German astronomer famous for his studies of the Moon.He was born at Marbach, in Württemberg, and brought up at Esslingen in poor circumstances. A self-taught mathematician, he had already published two original geometrical works when, in 1746, he entered J.B. Homann's...
- J T BürgJohann Tobias BürgJohann Tobias Bürg was an Austrian astronomer.Born in Vienna, Bürg worked as a professor and astronomer in Klagenfurt, in Carinthia. He subsequently worked as astronomical assistant at the observatory at Vienna from 1792 until he retired in 1813.He published some astronomical tables on the Moon...
- P S LaplacePierre-Simon LaplacePierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
- J K BurckhardtJohann Karl BurckhardtJohann Karl Burckhardt was a German-born astronomer and mathematician who later became a naturalized French citizen....
- P A HansenPeter Andreas HansenPeter Andreas Hansen was a Danish astronomer, was born at Tønder, Schleswig.-Biography:The son of a goldsmith, Hansen learned the trade of a watchmaker at Flensburg, and exercised it at Berlin and Tønder, 1818–1820...
- C DelaunayCharles-Eugène DelaunayCharles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
- E W BrownErnest William BrownErnest William Brown FRS was a British mathematician and astronomer, who spent the majority of his career working in the United States....
- W J EckertWallace John EckertWallace John Eckert was an American astronomer, who directed the Thomas J. Watson Astronomical Computing Bureau at Columbia University which evolved into the research division of IBM.-Life:...
- Jean Chapront & Michelle Chapront-Touzé
and other notable mathematical astronomers also made significant contributions, including: Edmond Halley
Edmond Halley
Edmond Halley FRS was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet. He was the second Astronomer Royal in Britain, following in the footsteps of John Flamsteed.-Biography and career:Halley...
; comte de Pontécoulant; J C Adams
John Couch Adams
John Couch Adams was a British mathematician and astronomer. Adams was born in Laneast, near Launceston, Cornwall, and died in Cambridge. The Cornish name Couch is pronounced "cooch"....
; G W Hill
George William Hill
George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
; and Simon Newcomb
Simon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
.
The history can be considered to fall into three parts: from ancient times to Newton; the period of classical (Newtonian) physics; and modern developments.
Babylon
Of Babylonian astronomy, practically nothing was known to historians of science before the 1880s. Surviving ancient writings of PlinyPliny the Elder
Gaius Plinius Secundus , better known as Pliny the Elder, was a Roman author, naturalist, and natural philosopher, as well as naval and army commander of the early Roman Empire, and personal friend of the emperor Vespasian...
had made bare mention of three astronomical schools in Mesopotamia
Mesopotamia
Mesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
– at Babylon, Uruk and 'Hipparenum' (possibly 'Sippar'). But definite modern knowledge of any details only began when J Epping
Joseph Epping
Joseph Epping was a German Jesuit astronomer and Assyriologist.-Life:...
deciphered cuneiform texts on clay tablets from a Babylonian archive: in these texts he identified an ephemeris of positions of the Moon. Since then, knowledge of the subject, still fragmentary, has had to be built up by painstaking analysis of deciphered texts, mainly in numerical form, on tablets from Babylon and Uruk (no trace has yet been found of anything from the third school mentioned by Pliny).
To the Babylon
Babylon
Babylon was an Akkadian city-state of ancient Mesopotamia, the remains of which are found in present-day Al Hillah, Babil Province, Iraq, about 85 kilometers south of Baghdad...
ian astronomer Kidinnu
Kidinnu
Kidinnu was a Chaldean astronomer and mathematician. Strabo of Amaseia called him Kidenas, Pliny the Elder Cidenas, and Vettius Valens Kidynas....
(in Greek or Latin, Kidenas or Cidenas) has been attributed the invention (5th or 4th century BC) of a system "B" for predicting the position of the moon, taking account that the moon continually changes its speed along its path relative to the background of fixed stars. This system involved calculating daily stepwise changes of lunar speed, up or down, with a minimum and a maximum approximately each month. The basis of these systems appears to have been arithmetical rather than geometrical, but they did approximately account for the main lunar inequality now known as the equation of the center
Equation of the center
For further closely related mathematical developments see also Two-body problem, also Gravitational two-body problem, also Kepler orbit, and Kepler problem...
.
The Babylonians appear to have been interested in calendars, new moons and eclipses. Some time between the years 500 BC and 400 BC they identified and began to use the 19-year cyclic relation between lunar months and solar years now known as the Metonic cycle
Metonic cycle
In astronomy and calendar studies, the Metonic cycle or Enneadecaeteris is a period of very close to 19 years which is remarkable for being very nearly a common multiple of the solar year and the synodic month...
.
They built up a numerical theory of the main irregularities in the Moon's motion, reaching remarkably good estimates for the (different) periods of the three most prominent features of the Moon's motion:-
- The synodic month, i.e. the mean period for the phases of the Moon. The so-called System B reckons the synodic month as 29 days and (sexagesimally) 3,11;0,50 time degrees (of 4 of our minutes): this converts to 29.530594 days = 29d 12h 44m 3.33s, to compare with a modern value (as at 1900 Jan 0) of 29.530589, or 29d 12h 44m 2.9s. This same value was used by Hipparchos and Ptolemy, was used throughout the Middle Ages, and still forms the basis of the Hebrew calendarHebrew calendarThe Hebrew calendar , or Jewish calendar, is a lunisolar calendar used today predominantly for Jewish religious observances. It determines the dates for Jewish holidays and the appropriate public reading of Torah portions, yahrzeits , and daily Psalm reading, among many ceremonial uses...
. - The mean lunar velocity relative to the stars they estimated at 13° 10' 35" per day, giving a corresponding month of 27.321598 days, to compare with modern values of 13° 10' 35.0275" and 27.321582.
- The anomalistic month, i.e. the mean period for the Moon's approximately monthly accelerations and decelerations in its rate of movement against the stars, had a Babylonian estimate of 27.5545833 days, to compare with a modern value 27.554551.
- The draconitic month, i.e. the mean period with which the path of the Moon against the stars deviates first north and then south in ecliptic latitude by comparison with the ecliptic path of the Sun, was indicated by a number of different parameters leading to various estimates, e.g. of 27.212204 days, to compare with a modern value of 27.212221, but the Babylonians also had a numerical relationship that 5458 synodic months were equal to 5923 draconitic months, which when compared with their accurate value for the synodic month leads to practically exactly the modern figure for the draconitic month.
The Babylonian estimate for the synodic month was adopted for the greater part of two millennia by Hipparchus, Ptolemy and medieval writers (and it is still in use as part of the basis for the calculated Hebrew (Jewish) calendar).
Greece and Hellenistic Egypt
Thereafter, from HipparchusHipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
and Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
down to the time of Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's work in the seventeenth century, lunar theories were composed mainly with the help of geometrical ideas, inspired more or less directly by long series of positional observations of the moon. Prominent in these geometrical lunar theories were combinations of circular motions – applications of the theory of epicycles. It wasn't until the work of Ibn al-Shatir
Ibn al-Shatir
Ala Al-Din Abu'l-Hasan Ali Ibn Ibrahim Ibn al-Shatir was an Arab Muslim astronomer, mathematician, engineer and inventor who worked as muwaqqit at the Umayyad Mosque in Damascus, Syria.-Astronomy:...
in the 14th century that the need for epicycles in lunar theory was eliminated.
Hipparchus
HipparchusHipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
, whose works are mostly lost and known mainly from quotations by other authors, assumed that the Moon moved in a circle inclined at 5° to the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
, rotating in a retrograde direction (i.e. opposite to the direction of annual and monthly apparent movements of the Sun and Moon relative to the fixed stars) once in 18 2/3 years. The circle acted as a deferent, carrying an epicycle along which the Moon was assumed to move in a retrograde direction. The center of the epicycle moved at a rate corresponding to the mean change in Moon's longitude, while the period of the Moon around the epicycle was an anomalistic month. This epicycle approximately provided for what was later recognized as the elliptical inequality, the equation of the center
Equation of the center
For further closely related mathematical developments see also Two-body problem, also Gravitational two-body problem, also Kepler orbit, and Kepler problem...
, and its size approximated to an equation of the center of about 5° 1'. This figure is much smaller than the modern value: but it is close to the difference between the modern coefficients of the equation of the center (1st term) and that of the evection: the difference is accounted for by the fact that the ancient measurements were taken at times of eclipses, and the effect of the evection (which subtracts under those conditions from the equation of the center) was at that time unknown and overlooked. For further information see also separate article Evection
Evection
Evection , in astronomy, is the largest inequality produced by the action of the Sun in the monthly revolution of the Moon around the Earth. The evection, formerly called the moon's second anomaly, was approximately known in ancient times, and its discovery is attributed to Ptolemy...
.
Ptolemy
PtolemyPtolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
's work the 'Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
' had wide and long-lasting acceptance and influence for over a millennium. He gave a geometrical lunar theory that improved on that of Hipparchus by providing for a second inequality of the Moon's motion, using a device that made the apparent apogee oscillate a little – 'prosneusis' of the epicycle. This 'second inequality' or 'second anomaly' accounted rather approximately, not only for the equation of the center, but also for what became known (much later) as the evection. But this theory, applied to its logical conclusion, would make the distance (and apparent diameter) of the Moon appear to vary by a factor of about 2, which is clearly not seen in reality. (The apparent angular diameter of the Moon does vary monthly, but only over a much narrower range of about 0.49-0.55°.) This defect of the Ptolemaic theory was part of what led to its eventual replacement in the 17th century.
Ibn al-Shatir and Copernicus
The most significant advance in lunar theory during medieval scienceScience in the Middle Ages
Science in the Middle Ages consisted of the study of nature, including practical disciplines, the mathematics and natural philosophy in medieval Europe. Following the fall of the Western Roman Empire and the decline in knowledge of Greek, Christian Western Europe was cut off from an important...
was made by the Arab astronomer, Ibn al-Shatir
Ibn al-Shatir
Ala Al-Din Abu'l-Hasan Ali Ibn Ibrahim Ibn al-Shatir was an Arab Muslim astronomer, mathematician, engineer and inventor who worked as muwaqqit at the Umayyad Mosque in Damascus, Syria.-Astronomy:...
(1304–1375), in the 14th century. Building on previous work carried out at the Maragheh observatory
Maragheh observatory
Maragheh observatory is an astronomical observatory which was established in 1259 CE by Nasir al-Din al-Tusi, an Iranian scientist and astronomer...
in the previous century as well as his own observations and experimental tests at the Umayyad Mosque
Umayyad Mosque
The Umayyad Mosque, also known as the Great Mosque of Damascus or formerly the Basilica of Saint John the Baptist , is located in the old city of Damascus, is one of the largest and oldest mosques in the world...
, he produced the first model of lunar motion that matched physical observations, and eliminated the need for any eccentric, epicycle
Deferent and epicycle
In the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
or equant
Equant
Equant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of heavenly bodies....
mechanisms that previous lunar models depended upon. This development in lunar theory was later employed by the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
astronomer Nicolaus Copernicus
Nicolaus Copernicus
Nicolaus Copernicus was a Renaissance astronomer and the first person to formulate a comprehensive heliocentric cosmology which displaced the Earth from the center of the universe....
, who used an identical lunar model to that of Ibn al-Shatir.
Tycho, Kepler and Horrocks
TychoTycho
Tycho may refer to:* Tycho Brahe , Danish nobleman and astronomer* Tycho van Meer , Dutch field hockey striker* Tommy Tycho , Hungarian-Australian pianist, conductor, composerIn astronomy:...
and Kepler refined the Ptolemaic lunar theory, but did not overcome its central defect of giving a poor account of the (mainly monthly) variations in the Moon's distance, apparent diameter and parallax. Their work added to the lunar theory three substantial further discoveries. (1) The nodes and the inclination of the lunar orbital plane both appear to librate, with a monthly (according to Tycho) or semi-annual period (according to Kepler). (2) The lunar longitude has a twice-monthly 'Variation', by which the Moon moves faster than expected at new and full moon, and slower than expected at the quarters. (3) There is also an annual effect, by which the lunar motion slows down a little in January and speeds up a little in July: the 'annual equation'.
The refinements of Tycho and Kepler were recognized by their immediate successors as improvements, but their seventeenth-century successors tried numerous alternative geometrical configurations for the lunar motions in order to improve matters further. A notable success was achieved by Jeremiah Horrocks
Jeremiah Horrocks
Jeremiah Horrocks , sometimes given as Jeremiah Horrox , was an English astronomer who was the only person to predict, and one of only two people to observe and record, the transit of Venus of 1639.- Life and work :Horrocks was born in Lower Lodge, in...
, who proposed a scheme involving an approximate 6-monthly libration in the position of the lunar apogee and also in the size of the elliptical eccentricity. This scheme had the great merit of giving a more realistic description of the changes in distance, diameter and parallax of the Moon.
Newton
A first gravitational period for lunar theory started with the work of NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
. He was the first to define the problem of the perturbed motion of the Moon in recognisably modern terms. His groundbreaking work is shown for example in the 'Principia' in all versions including the first edition published in 1687.
Solar perturbation of lunar motion
Newton identified how to evaluate the perturbing effect on the relative motion of the Earth and Moon, arising from their gravity towards the Sun, in Book 1, Proposition 66, and in Book 3, Proposition 25. The starting-point for this approach is Corollary VI to the laws of motion. This shows that if the external accelerative forces from some massive body happens to act equally and in parallel on some different other bodies considered, then those bodies would be affected equally, and in that case their motions (relative to each other) would continue as if there were no such external accelerative forces at all. It is only in the case that the external forces (e.g. in Book 1, Prop.66, and Book 3, Prop.25, the gravitational attractions towards the Sun) are different in size or in direction in their accelerative effects on the different bodies considered (e.g. on the Earth and Moon), that consequent effects are appreciable on the relative motions of the latter bodies. (Newton referred to 'accelerative forces' or 'accelerative gravity' due to some external massive attractor such as the Sun. The measure he used was the acceleration that the force tends to produce (in modern terms, force per unit mass), rather than what we would now call the force itself.)Thus Newton concluded that it is only the difference between the Sun's accelerative attraction on the Moon and the Sun's attraction on the Earth that perturbs the motion of the Moon relative to the Earth.
Newton then in effect used vector decomposition
Vector decomposition
Vector decomposition refers to decomposing a vector of Rn into several vectors, each linearly independent .-Vector decomposition in two dimensions:...
of forces, to carry out this analysis. In Book 1, Proposition 66 and in Book 3, Proposition 25, he showed by a geometrical construction, starting from the total gravitational attraction of the Sun on the Earth, and of the Sun on the Moon, the difference that represents the perturbing effect on the motion of the Moon relative to the Earth. In summary, line LS in Newton's diagram as shown below represents the size and direction of the perturbing acceleration acting on the Moon in the Moon's current position P (line LS does not pass through point P, but the text shows that this is not intended to be significant, it is a result of the scale factors and the way the diagram has been built up).
Shown here is Newton's diagram from the first (1687) Latin edition of the Principia (Book 3, Proposition 25, at p. 434). Here he introduced his analysis of perturbing accelerations on the Moon in the Sun-Earth-Moon system. Q represents the Sun, S the Earth, and P the Moon.
Parts of this diagram represent distances, other parts gravitational accelerations (attractive forces per unit mass). In a dual significance, SQ represents the Earth-Sun distance, and then it also represents the size and direction of the Earth-Sun gravitational acceleration. Other distances in the diagram are then in proportion to distance SQ. Other attractions are in proportion to attraction SQ.
The Sun's attractions are SQ (on the Earth) and LQ (on the Moon). The size of LQ is drawn so that the ratio of attractions LQ:SQ is the inverse square of the ratio of distances PQ:SQ. (Newton constructs KQ=SQ, giving an easier view of the proportions.) The Earth's attraction on the Moon acts along direction PS. (But line PS signifies only distance and direction so far, nothing has been defined about the scale factor between solar and terrestrial attractions).
After showing solar attractions LQ on the Moon and SQ on the Earth, on the same scale, Newton then makes a vector decomposition of LQ into components LM and MQ. Then he identifies the perturbing acceleration on the Moon as the difference of this from SQ. SQ and MQ are parallel to each other, so SQ can be directly subtracted from MQ, leaving MS. The resulting difference, after subtracting SQ from LQ, is therefore the vector sum of LM and MS: these add up to a perturbing acceleration LS.
Later Newton identified another resolution of the perturbing acceleration LM+MS = LS, into orthogonal components: a transverse component parallel to LE, and a radial component, effectively ES.
Newton's diagrammatic scheme, since his time, has been re-presented in other and perhaps visually clearer ways. Shown here is a vector presentation indicating, for two different positions, P1 and P2, of the Moon in its orbit around the Earth, the respective vectors LS1 and LS2 for the perturbing acceleration due to the Sun. The Moon's position at P1 is fairly close to what it was at P in Newton's diagram; corresponding perturbation LS1 is like Newton's LS in size and direction. At another position P2, the Moon is farther away from the Sun than the Earth is, the Sun's attraction LQ2 on the Moon is weaker than the Sun's attraction SQ=SQ2 on the Earth, and then the resulting perturbation LS2 points obliquely away from the Sun.
Quadrature (astronomy)
In astronomy, quadrature is that aspect of a heavenly body in which it makes a right angle with the direction of the Sun. It is applied especially to the apparent position of a superior planet, or of the Moon at first and last quarters....
where it adds to the Earth's attraction he put it at 1/178.725 of the mean terrestrial attraction, and twice as much as that at the new and full moons where it opposes and diminishes the Earth's attraction.)
Newton also showed that the same pattern of perturbation applies, not only to the Moon, in its relation to the Earth as disturbed by the Sun, but also to other particles more generally in their relation to the solid Earth as disturbed by the Sun (or by the Moon); for example different portions of the tidal waters at the Earth's surface. The study of the common pattern of these perturbing accelerations grew out of Newton's initial study of the perturbations of the Moon, which he also applied to the forces moving tidal waters. Nowadays this common pattern itself has become often known as a tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
whether it is being applied to the disturbances of the motions of the Moon, or of the Earth's tidal waters – or of the motions of any other object that suffers perturbations of analogous pattern.
After introducing his diagram 'to find the force of the Sun to perturb the Moon' in Book 3, Proposition 25, Newton developed a first approximation to the solar perturbing force, showing in further detail how its components vary as the Moon follows its monthly path around the Earth. He also took the first steps in investigating how the perturbing force shows its effects by producing irregularities in the lunar motions. (In this part of the enterprise, Newton's success was more limited: it is relatively uncomplicated to define the perturbing forces, but heavy complexities soon arise in the problem of working out the resulting motions, and these were to challenge mathematical astronomers for two centuries after Newton's initial definition of the problem and indication of the directions to take in solving it.)
For a selected few of the lunar inequalities, Newton showed in some quantitative detail how they arise from the solar perturbing force.
Much of this lunar work of Newton's was done in the 1680s, and the extent and accuracy of his first steps in the gravitational analysis was limited by several factors, including his own choice to develop and present the work in what was, on the whole, a difficult geometrical way, and by the limited accuracy and uncertainty of many astronomical measurements in his time.
Classical gravitational period after Newton
The main aim of Newton's successors, from Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, Alexis Clairaut and Jean d'Alembert in the mid-eighteenth century, down to E W Brown
Ernest William Brown
Ernest William Brown FRS was a British mathematician and astronomer, who spent the majority of his career working in the United States....
in the late nineteenth and early twentieth century, was to account completely and much more precisely for the moon's motions on the basis of Newton's laws, i.e. the laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and of universal gravitation by attractions inversely proportional to the squares of the distances between the attracting bodies. They also wished to put the inverse-square law of gravitation to the test, and for a time in the 1740s it was seriously doubted, on account of what was then thought to be a large discrepancy between the Newton-theoretical and the observed rates in the motion of the lunar apogee. However Clairaut showed shortly afterwards (1749–50) that at least the major cause of the discrepancy lay not in the lunar theory based on Newton's laws, but in excessive approximations that he and others had relied on to evaluate it.
Most of the improvements in theory after Newton were made in algebraic form: they involved voluminous and highly laborious amounts of infinitesimal calculus and trigonometry. It also remained necessary, for completing the theories of this period, to refer to observational measurements.
Results of the theories
The lunar theorists used (and invented) many different mathematical approaches to analyse the gravitational problem. Not surprisingly, their results tended to converge. From the time of the earliest gravitational analysts among Newton's successors, EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, Clairaut and d'Alembert, it was recognized that nearly all of the main lunar perturbations could be expressed in terms of just a few angular arguments and coefficients. These can be represented by:
- the mean motions or positions of the Moon and the Sun, together with three coefficients and three angular positions, which together define the shape and location of their apparent orbits:
- the two eccentricities (
, about 0.0549, and 
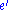, about 0.01675) of the ellipses that approximate to the apparent orbits of the Moon and the Sun; - the angular direction of the perigees (
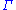and 
) (or their opposite points the apogees) of the two orbits; and - the angle of inclination (
, mean value about 18523") between the planes of the two orbits, together with the direction (
) of the line of nodes in which those two planes intersect. The ascending node (
) is the node passed by the Moon when it is tending northwards relative to the ecliptic.
From these basic parameters, just four basic differential angular arguments are enough to express, in their different combinations, nearly all of the most significant perturbations of the lunar motions. They are given here with their conventional symbols due to Delaunay
Charles-Eugène Delaunay
Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
; they are sometimes known as the Delaunay arguments:
-
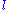the Moon's mean anomaly (distance of the mean longitude of the Moon from the mean longitude of its perigee 
); -
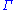the Sun's mean anomaly (distance of the mean longitude of the Sun from the mean longitude of its perigee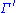 
); -
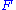the Moon's mean argument of latitude (distance of the mean longitude of the Moon from the mean longitude of its ascending (northward-bound) node 
); -
the Moon's mean (solar) elongation (distance of the mean longitude of the Moon from the mean longitude of the Sun).
This work culminated into Brown´s
Ernest William Brown
Ernest William Brown FRS was a British mathematician and astronomer, who spent the majority of his career working in the United States....
lunar theory (1897..1908) and Tables of the Motion of the Moon (1919). These were used in the American Ephemeris and Nautical Almanac
American Ephemeris and Nautical Almanac
The American Ephemeris and Nautical Almanac was published for the years 1855 to 1980, containing information necessary for astronomers, surveyors, and navigators...
until 1968, and in a modified form until 1984.
Largest or named lunar inequalities
Several of the largest lunar perturbations in longitude (contributions to the difference in its true ecliptic longitude relative to its mean longitude) have been named. In terms of the differential arguments, they can be expressed in the following way, with coefficients rounded to the nearest second of arc ("):Equation of the center
- The Moon's equation of the center, or elliptic inequality, was known at least in approximation, to the ancients from the Babylonians and Hipparchus onwards. Knowledge of more recent date is that it corresponds to the approximate application of Kepler's law of equal areas in an elliptical orbit, and represents the speeding-up of the Moon as its distance from the Earth decreases while it moves towards its perigee, and then its slowing down as its distance from the Earth increases while it moves towards its apogee. The effect on the Moon's longitude can be approximated by a series of terms, of which the first three are
.
Evection
- The evection (or its approximation) was known to Ptolemy, but its name and knowledge of its cause dates from the 17th century. Its effect on the Moon's longitude has an odd-appearing period of about 31.8 days. This can be represented in a number of ways, for example as the result of an approximate 6-monthly libration in the position of perigee, with an accompanying 6-monthly pulsation in the size of the Moon's orbital eccentricity. Its principal term is
.
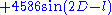Variation
- The Variation, discovered by Tycho, is a speeding-up of the Moon as it approaches new-moon and full-moon, and a slowing-down as it approaches first and last quarter. Its gravitational explanation with a quantitative estimate was first given by Newton. Its principal term is
.
Annual equation
- The annual equation, also discovered by Tycho, was qualitatively explained by Newton in terms that the Moon's orbit becomes slightly expanded in size, and longer in period, when the Earth is at perihelion closest to the Sun at the beginning of January, and the Sun's perturbing effect is strongest, and then slightly contracted in size and shorter in period when the Sun is most distant in early July, so that its perturbing effect is weaker: the modern value for the principal term due to this effect is
.
Parallactic Inequality
- The parallactic inequality, first found by Newton, makes Tycho's Variation a little asymmetric as a result of the finite distance and non-zero parallax of the Sun. Its effect is that the Moon is a little behind at first quarter, and a little ahead at last quarter. Its principal term is
.
Reduction to the Ecliptic
- The reduction to the ecliptic represents the geometric effect of expressing the Moon's motion in terms of a longitude in the plane of the ecliptic, although its motion is really taking place in a plane that is inclined by about 5 degrees. Its principal term is
.
The analysts of the mid-18th century expressed the perturbations of the Moon's position in longitude using about 25-30 trigonometrical terms. The number of terms needed to express the Moon's position with the accuracy sought at the beginning of the twentieth century was over 1400; and the number of terms needed to emulate the accuracy of modern numerical integrations based on laser-ranging observations is in the tens of thousands: there is no limit to the increase in number of terms needed as requirements of accuracy increase.
Digital Computers and Lunar Laser Ranging
Since the second world war and especially since the 1960s, lunar theory has been further developed in a somewhat different way. This has been stimulated on the one hand, by the use of automatic digital computation, and on the other hand, by modern observational data-types, with greatly increased accuracy and precision.Wallace John Eckert
Wallace John Eckert
Wallace John Eckert was an American astronomer, who directed the Thomas J. Watson Astronomical Computing Bureau at Columbia University which evolved into the research division of IBM.-Life:...
, a student of Brown who worked at IBM, used the experimental digital computers developed there after the second world war for computation of astronomical ephemerides. One of the projects was to put Brown's lunar theory into the machine and evaluate the expressions directly. Another project was something entirely new: a numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
of the equations of motion for the Sun and the four major planets. This became feasible only after electronic digital computers became available. Eventually this led to the Jet Propulsion Laboratory Development Ephemeris series.
In the mean time, Brown's theory was improved with better constants and the introduction of Ephemeris Time
Ephemeris time
The term ephemeris time can in principle refer to time in connection with any astronomical ephemeris. In practice it has been used more specifically to refer to:...
and the removal of some empirical corrections associated with this. This led to the Improved Lunar Ephemeris (ILE), which, with some minor successive improvements, was used in the astronomical almanacs from 1960 through 1983 (ILE j=0 from 1960 to 1967, ILE j=1 from 1968 to 1971, ILE j=2 from 1972 to 1983), and was used to bring men to the moon.
The most significant improvement of position observations of the moon have been the lunar laser ranging measurements, obtained using earth-bound lasers and special retro-reflectors placed on the surface of the moon. The time-of-flight of a pulse of laser light to one of the reflectors and back gives a measure of the moon's distance at that time. The first of four reflectors which are still operational today was taken to the moon in the Apollo 11
Apollo 11
In early 1969, Bill Anders accepted a job with the National Space Council effective in August 1969 and announced his retirement as an astronaut. At that point Ken Mattingly was moved from the support crew into parallel training with Anders as backup Command Module Pilot in case Apollo 11 was...
spacecraft in July 1969 and placed in suitable position on the Moon's surface by Neil Armstrong
Neil Armstrong
Neil Alden Armstrong is an American former astronaut, test pilot, aerospace engineer, university professor, United States Naval Aviator, and the first person to set foot upon the Moon....
.
The precision of this science
Lunar laser ranging experiment
The ongoing Lunar Laser Ranging Experiment measures the distance between the Earth and the Moon using laser ranging. Lasers on Earth are aimed at retroreflectors planted on the moon during the Apollo program, and the time for the reflected light to return is determined...
is currently being extended still further by the recently-established Apache Point Observatory Lunar Laser-ranging Operation
Apache Point Observatory Lunar Laser-ranging Operation
The Apache Point Observatory Lunar Laser-ranging Operation, or APOLLO, is a project at the Apache Point Observatory in New Mexico. It is an extension and advancement of previous Lunar Laser Ranging Experiment, which uses retroreflectors on the Moon to track changes in lunar orbital distance and...
.
Numerical Integrations, Relativity, Tides, Librations
The lunar theory, as developed numerically to fine precision using these modern measures, is based on a larger range of considerations than the classical theories: it takes account not only of gravitational forces (with relativistic corrections) but also of many tidal and geophysical effects and a greatly extended theory of lunar librations. Like many other scientific fields this one has now developed so as to be based on the work of large teams and institutions. An institution notably taking one of the leading parts in these developments has been the Jet Propulsion LaboratoryJet Propulsion Laboratory
Jet Propulsion Laboratory is a federally funded research and development center and NASA field center located in the San Gabriel Valley area of Los Angeles County, California, United States. The facility is headquartered in the city of Pasadena on the border of La Cañada Flintridge and Pasadena...
at California Institute of Technology
California Institute of Technology
The California Institute of Technology is a private research university located in Pasadena, California, United States. Caltech has six academic divisions with strong emphases on science and engineering...
; and names particularly associated with the transition, from the early 1970s onwards, from classical lunar theories and ephemerides towards the modern state of the science include those of J Derral Mulholland and J G Williams (and for the linked development of solar system (planetary) ephemerides E Myles Standish).
Since the 1970s, the Jet Propulsion Laboratory
Jet Propulsion Laboratory
Jet Propulsion Laboratory is a federally funded research and development center and NASA field center located in the San Gabriel Valley area of Los Angeles County, California, United States. The facility is headquartered in the city of Pasadena on the border of La Cañada Flintridge and Pasadena...
(JPL) has produced a series of numerically integrated Development Ephemerides (numbered DExxx), incorporating Lunar Ephemerides (LExxx). Planetary and lunar ephemerides DE200/LE200 were used in the official Astronomical Almanac ephemerides for 1984–2002, and ephemerides DE405/LE405, of further improved accuracy and precision, have been in use as from the issue for 2003.U S Naval Observatory (2009) History of the Astronomical Almanac.
Analytical developments
In parallel with these developments, a new class of analytical lunar theory has also been developed in recent years, notably the Ephemeride Lunaire ParisienneEphemeride Lunaire Parisienne
Éphéméride Lunaire Parisienne is a lunar theory developed by Jean Chapront, Michelle Chapront-Touzé, and others at the Bureau des Longitudes in the 1970s to 1990s.ELP gives a series expansion of the orbital elements and the coordinates of the Moon...
by Jean Chapront and Michelle Chapront-Touzé from the Bureau des Longitudes
Bureau des Longitudes
The Bureau des Longitudes is a French scientific institution, founded by decree of 25 June 1795 and charged with the improvement of nautical navigation, standardisation of time-keeping, geodesy and astronomical observation. During the 19th century, it was responsible for synchronizing clocks...
. Using computer-assisted algebra, the analytical developments have been taken further than previously could be done by the classical analysts working manually. Also, some of these new analytical theories (like ELP) have been fitted to the numerical ephemerides previously developed at JPL as mentioned above. The main aims of these recent analytical theories, in contrast to the aims of the classical theories of past centuries, have not been to generate improved positional data for current dates; rather, their aims have included the study of further aspects of the motion, such as long-term properties, which may not so easily be apparent from the modern numerical theories themselves.