Luke's variational principle
Encyclopedia
In fluid dynamics
, Luke's variational principle is a Lagrangian
variational description of the motion of surface waves
on a fluid
with a free surface
, under the action of gravity
. This principle is named after J.C. Luke, who published it in 1967. This variational principle is for incompressible and inviscid potential flow
s, and is used to derive approximate wave models like the so-called mild-slope equation
, or using the average-Lagrangian approach for wave propagation in inhomogeneous media.
Luke's Lagrangian formulation can also be recast into a Hamiltonian
formulation in terms of the surface elevation and velocity potential at the free surface. This is often used when modelling the spectral density
evolution of the free-surface in a sea state
, sometimes called wave turbulence
.
Both the Lagrangian and Hamiltonian formulations can be extended to include surface tension
effects.
formulation is for non-linear surface gravity waves on an—incompressible, irrotational and inviscid
—potential flow
.
The relevant ingredients, needed in order to describe this flow, are:
The Lagrangian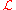
, as given by Luke, is:
From Bernoulli's principle
, this Lagrangian can be seen to be the integral
of the fluid pressure
over the whole time-dependent fluid domain V(t). This is in agreement with the variational principles for inviscid flow without a free surface, found by Harry Bateman
.
Variation
with respect to the velocity potential Φ(x,z,t) and free-moving surfaces like z=η(x,t) results in the Laplace equation for the potential in the fluid interior and all required boundary conditions: kinematic boundary conditions on all fluid boundaries and dynamic
boundary conditions on free surfaces. This may also include moving wavemaker walls and ship motion.
For the case of a horizontally unbounded domain with the free fluid surface at z=η(x,t) and a fixed bed at z=−h(x), Luke's variational principle results in the Lagrangian:
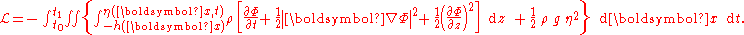
The bed-level term proportional to h2 in the potential energy has been neglected, since it is a constant and does not contribute in the variations.
Below, Luke's variational principle is used to arrive at the flow equations for non-linear surface gravity waves on a potential flow.
in the Lagrangian with respect to variations in the velocity potential Φ(x,z,t), as well as with respect to the surface elevation η(x,t), have to be zero. We consider both variations subsequently.
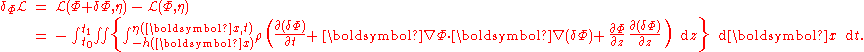
Using Leibniz integral rule
, this becomes, in case of constant density ρ:
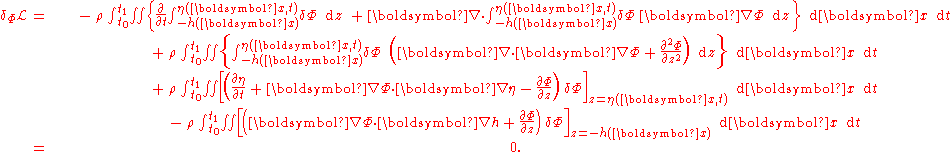
The first integral on the right-hand side integrates out to the boundaries, in x and t, of the integration domain and is zero since the variations δΦ are taken to be zero at these boundaries. For variations δΦ which are zero at the free surface and the bed, the second integral remains, which is only zero for arbitrary δΦ in the fluid interior if there the Laplace equation holds:
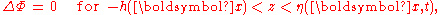
with Δ=∇·∇ + ∂2/∂z2 the Laplace operator
.
If variations δΦ are considered which are only non-zero at the free surface, only the third integral remains, giving rise to the kinematic free-surface boundary condition:
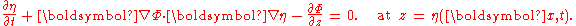
Similarly, variations δΦ only non-zero at the bottom z = -h result in the kinematic bed condition:
This has to be zero for arbitrary δη, giving rise to the dynamic boundary condition at the free surface:
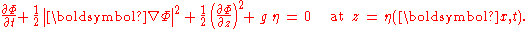
This is the Bernoulli equation
for unsteady potential flow, applied at the free surface, and with the pressure above the free surface being a constant — which constant pressure is taken equal to zero for simplicity.
structure of surface gravity waves on a potential flow was discovered by Vladimir E. Zakharov
in 1968, and rediscovered independently by Bert Broer
and John Miles
:
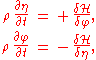
where the surface elevation η and surface potential φ — which is the potential Φ at the free surface z=η(x,t) — are the canonical variables
. The Hamiltonian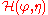
is the sum of the kinetic
and potential energy
of the fluid:
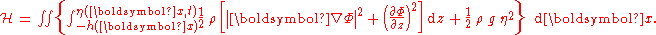
The additional constraint is that the flow in the fluid domain has to satisfy Laplace's equation
with appropriate boundary condition at the bottom z=-h(x) and that the potential at the free surface z=η is equal to φ: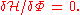
on the integral of ∂Φ/∂t:
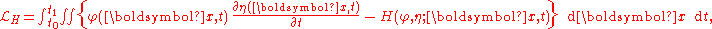
with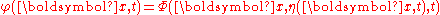
the value of the velocity potential at the free surface, and 
the Hamiltonian density — sum of the kinetic and potential energy density — and related to the Hamiltonian as:
The Hamiltonian density is written in terms of the surface potential using Green's third identity
on the kinetic energy:
where D(η) φ is equal to the normal
derivative of ∂Φ/∂n at the free surface. Because of the linearity of the Laplace equation — valid in the fluid interior and depending on the boundary condition at the bed z=-h and free surface z=η — the normal derivative ∂Φ/∂n is a linear function of the surface potential φ, but depends non-linear on the surface elevation η. This is expressed by the Dirichlet-to-Neumann
operator D(η), acting linearly on φ.
The Hamiltonian density can also be written as:
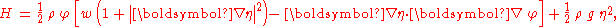
with w(x,t) = ∂Φ/∂z the vertical velocity at the free surface z = η. Also w is a linear function of the surface potential φ through the Laplace equation, but w depends non-linear on the surface elevation η:
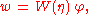
with W operating linear on φ, but being non-linear in η. As a result, the Hamiltonian is a quadratic functional
of the surface potential φ. Also the potential energy part of the Hamiltonian is quadratic. The source of non-linearity in surface gravity waves is through the kinetic energy depending non-linear on the free surface shape η.
Further ∇φ is not to be mistaken for the horizontal velocity ∇Φ at the free surface:
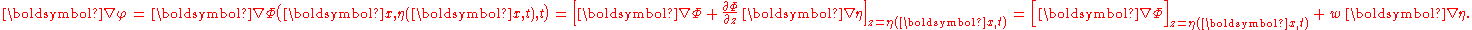
Taking the variations of the Lagrangian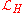
with respect to the canonical variables 
and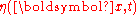 
gives:
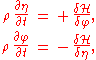
provided in the fluid interior Φ satisfies the Laplace equation, ΔΦ=0, as well as the bottom boundary condition at z=-h and Φ=φ at the free surface.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, Luke's variational principle is a Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
variational description of the motion of surface waves
Ocean surface wave
In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
on a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
with a free surface
Free surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
, under the action of gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
. This principle is named after J.C. Luke, who published it in 1967. This variational principle is for incompressible and inviscid potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
s, and is used to derive approximate wave models like the so-called mild-slope equation
Mild-slope equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave...
, or using the average-Lagrangian approach for wave propagation in inhomogeneous media.
Luke's Lagrangian formulation can also be recast into a Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
formulation in terms of the surface elevation and velocity potential at the free surface. This is often used when modelling the spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
evolution of the free-surface in a sea state
Sea state
In oceanography, a sea state is the general condition of the free surface on a large body of water—with respect to wind waves and swell—at a certain location and moment. A sea state is characterized by statistics, including the wave height, period, and power spectrum. The sea state varies with...
, sometimes called wave turbulence
Wave turbulence
Wave turbulence is a set of waves deviated far from thermal equilibrium. Such state is accompanied by dissipation. It is either decaying turbulence or requires external source of energy to sustain it...
.
Both the Lagrangian and Hamiltonian formulations can be extended to include surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
effects.
Luke's Lagrangian
Luke's LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
formulation is for non-linear surface gravity waves on an—incompressible, irrotational and inviscid
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
—potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
.
The relevant ingredients, needed in order to describe this flow, are:
- Φ(x,z,t) is the velocity potential,
- ρ is the fluid densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, - g is the acceleration by the Earth's gravityEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
, - x is the horizontal coordinate vector with components x and y,
- x and y are the horizontal coordinates,
- z is the vertical coordinate,
- t is time, and
- ∇ is the horizontal gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator, so ∇Φ is the horizontal flow velocityFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
consisting of ∂Φ/∂x and ∂Φ/∂y, - V(t) is the time-dependent fluid domain with free surface.
The Lagrangian
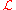, as given by Luke, is:From Bernoulli's principle
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
, this Lagrangian can be seen to be the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the fluid pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
over the whole time-dependent fluid domain V(t). This is in agreement with the variational principles for inviscid flow without a free surface, found by Harry Bateman
Harry Bateman
Harry Bateman FRS was an English mathematician.-Life and work:Harry Bateman first grew to love mathematics at Manchester Grammar School, and in his final year, won a scholarship to Trinity College, Cambridge. There he distinguished himself in 1903 as Senior Wrangler and by winning the Smith's Prize...
.
Variation
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
with respect to the velocity potential Φ(x,z,t) and free-moving surfaces like z=η(x,t) results in the Laplace equation for the potential in the fluid interior and all required boundary conditions: kinematic boundary conditions on all fluid boundaries and dynamic
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
boundary conditions on free surfaces. This may also include moving wavemaker walls and ship motion.
For the case of a horizontally unbounded domain with the free fluid surface at z=η(x,t) and a fixed bed at z=−h(x), Luke's variational principle results in the Lagrangian:
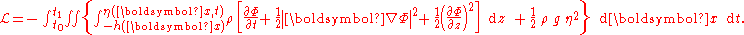
The bed-level term proportional to h2 in the potential energy has been neglected, since it is a constant and does not contribute in the variations.
Below, Luke's variational principle is used to arrive at the flow equations for non-linear surface gravity waves on a potential flow.
Derivation of the flow equations resulting from Luke's variational principle
The variation in the Lagrangian with respect to variations in the velocity potential Φ(x,z,t), as well as with respect to the surface elevation η(x,t), have to be zero. We consider both variations subsequently.Variation with respect to the velocity potential
Consider a small variation δΦ in the velocity potential Φ. Then the resulting variation in the Lagrangian is: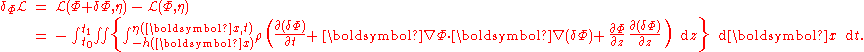Using Leibniz integral rule
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
, this becomes, in case of constant density ρ:
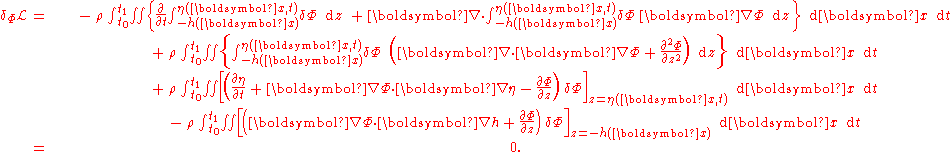
The first integral on the right-hand side integrates out to the boundaries, in x and t, of the integration domain and is zero since the variations δΦ are taken to be zero at these boundaries. For variations δΦ which are zero at the free surface and the bed, the second integral remains, which is only zero for arbitrary δΦ in the fluid interior if there the Laplace equation holds:
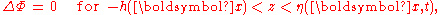
with Δ=∇·∇ + ∂2/∂z2 the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
If variations δΦ are considered which are only non-zero at the free surface, only the third integral remains, giving rise to the kinematic free-surface boundary condition:
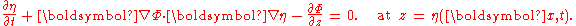
Similarly, variations δΦ only non-zero at the bottom z = -h result in the kinematic bed condition:
Variation with respect to the surface elevation
Considering the variation of the Lagrangian with respect to small changes δη gives:This has to be zero for arbitrary δη, giving rise to the dynamic boundary condition at the free surface:
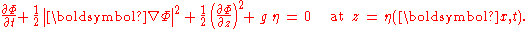
This is the Bernoulli equation
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
for unsteady potential flow, applied at the free surface, and with the pressure above the free surface being a constant — which constant pressure is taken equal to zero for simplicity.
Hamiltonian formulation
The HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
structure of surface gravity waves on a potential flow was discovered by Vladimir E. Zakharov
Vladimir E. Zakharov
Vladimir Evgen'evich Zakharov is a Soviet and Russian mathematician and physicist. He is currently Regents' Professor of mathematics at The University of Arizona and director of the Mathematical Physics Sector at the Lebedev Physical Institute...
in 1968, and rediscovered independently by Bert Broer
Lambertus Johannes Folkert Broer
Lambertus Johannes Folkert "Bert" Broer was a Dutch physicist and mathematician.- External links :...
and John Miles
John W. Miles
John Wilder Miles was a research professor emeritus of applied mechanics and geophysics at Scripps Institution of Oceanography, University of California, San Diego...
:
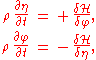
where the surface elevation η and surface potential φ — which is the potential Φ at the free surface z=η(x,t) — are the canonical variables
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
. The Hamiltonian
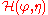is the sum of the kineticKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of the fluid:
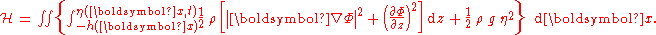
The additional constraint is that the flow in the fluid domain has to satisfy Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
with appropriate boundary condition at the bottom z=-h(x) and that the potential at the free surface z=η is equal to φ:
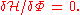
Relation with Lagrangian formulation
The Hamiltonian formulation can be derived from Luke's Lagrangian description by using Leibniz integral ruleLeibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
on the integral of ∂Φ/∂t:
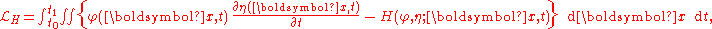
with
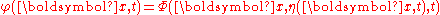the value of the velocity potential at the free surface, and the Hamiltonian density — sum of the kinetic and potential energy density — and related to the Hamiltonian as:The Hamiltonian density is written in terms of the surface potential using Green's third identity
Green's identities
In mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.-Green's first identity:...
on the kinetic energy:
where D(η) φ is equal to the normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
derivative of ∂Φ/∂n at the free surface. Because of the linearity of the Laplace equation — valid in the fluid interior and depending on the boundary condition at the bed z=-h and free surface z=η — the normal derivative ∂Φ/∂n is a linear function of the surface potential φ, but depends non-linear on the surface elevation η. This is expressed by the Dirichlet-to-Neumann
Poincaré–Steklov operator
In mathematics, a Poincaré–Steklov operator maps the values of one boundary condition of the solution of an elliptic partial differential equation in a domain to the values of another boundary condition. Usually, either of the boundary conditions determines the solution...
operator D(η), acting linearly on φ.
The Hamiltonian density can also be written as:
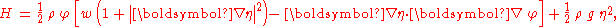
with w(x,t) = ∂Φ/∂z the vertical velocity at the free surface z = η. Also w is a linear function of the surface potential φ through the Laplace equation, but w depends non-linear on the surface elevation η:
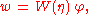
with W operating linear on φ, but being non-linear in η. As a result, the Hamiltonian is a quadratic functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the surface potential φ. Also the potential energy part of the Hamiltonian is quadratic. The source of non-linearity in surface gravity waves is through the kinetic energy depending non-linear on the free surface shape η.
Further ∇φ is not to be mistaken for the horizontal velocity ∇Φ at the free surface:
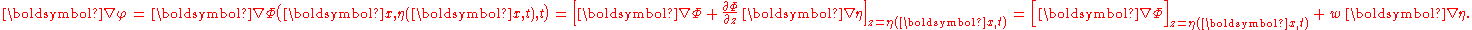
Taking the variations of the Lagrangian
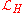with respect to the canonical variables and 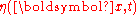gives: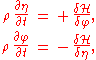provided in the fluid interior Φ satisfies the Laplace equation, ΔΦ=0, as well as the bottom boundary condition at z=-h and Φ=φ at the free surface.