Loop-erased random walk
Encyclopedia
In mathematics
, loop-erased random walk is a model for a random simple path
with important applications in combinatorics
and, in physics
, quantum field theory
. It is intimately connected to the uniform spanning tree, a model for a random tree
. See also random walk
for more general treatment of this topic.
and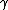
is some path
of length n on G. In other words,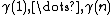
are vertices of G such that 
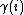and 
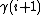are neighbors. Then the loop erasure of 
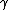is a new simple path created by erasing all the loops of 
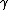in chronological order. Formally, we define indices 
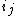inductively
using
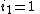
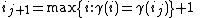
where "max" here means up to the length of the path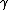
. The induction stops when for some 
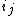we have 
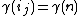. Assume this happens at J i.e. 
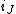is the last 
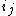. Then the loop erasure of 
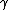, denoted by 
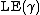is a simple path of length J defined by
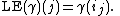
Now let G be some graph, let v be a vertex of G, and let R be a random walk on G starting from v. Let T be some stopping time for R. Then the loop-erased random walk until time T is LE(R([1,T])). In other words, take R from its beginning until T — that's a (random) path — erase all the loops in chronological order as above — you get a random simple path.
The stopping time T may be fixed, i.e. one may perform n steps and then loop-erase. However, it is usually more natural to take T to be the hitting time
in some set. For example, let G be the graph Z2 and let R be a random walk starting from the point (0,0). Let T be the time when R first hits the circle of radius 100 (we mean here of course a discretized circle). LE(R) is called the loop-erased random walk starting at (0,0) and stopped at the circle.
of G is a subgraph of G containing all vertices and some of the edges, which is a tree
, i.e. connected and with no cycles. The uniform spanning tree (UST for short) is a random spanning tree chosen among all the possible spanning trees of G with equal probability.
Let now v and w be two vertices in G. Any spanning tree contains precisely one simple path between v and w. Taking this path in the uniform spanning tree gives a random simple path. It turns out that the distribution of this path is identical to the distribution of the loop-erased random walk starting at v and stopped at w.
An immediate corollary is that loop-erased random walk is symmetric in its start and end points. More precisely, the distribution of the loop-erased random walk starting at v and stopped at w is identical to the distribution of the reversal of loop-erased random walk starting at w and stopped at v. This is not a trivial fact at all! Loop-erasing a path and the reverse path do not give the same result. It is only the distributions that are identical.
A-priori sampling
a UST seems difficult. Even a relatively modest graph (say a 100x100 grid) has way too many spanning trees to prepare a complete list. Therefore a different approach is needed. There are a number of algorithms for sampling a UST, but we will concentrate on Wilson's algorithm.
Take any two vertices and perform loop-erased random walk from one to the other. Now take a third vertex (not on the constructed path) and perform loop-erased random walk until hitting the already constructed path. This gives a tree with three leaves. Choose a fourth vertex and do loop-erased random walk until hitting this tree. Continue until the tree spans all the vertices. It turns out that no matter which method you use to choose the starting vertices you always end up with the same distribution on the spanning trees, namely the uniform one.
Laplace equation. Let again G be a graph and let v and w be two vertices in G. Construct a random path from v to w inductively using the following procedure. Assume we have already defined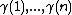
. Let f be a function from G to R satisfying
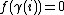for all 
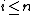and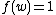 
Where a function f on a graph is discretely harmonic at a point x if f(x) equals the average of f on the neighbors of x.
With f defined choose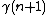
using f at the neighbors of 
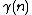as weights. In other words, if 
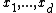are these neighbors, choose 
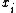with probability
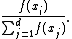
Continue this process, (notice that at each step you have to calculate f again) and you will end up with a random simple path from v to w. It turns out that the distribution of this path is identical to that of a loop-erased random walk from v to w.
An alternative view is that the distribution of a loop-erased random walk conditioned
to start in some path β is identical to the loop-erasure of a random walk conditioned not to hit β. This property is often referred to as the Markov property of loop-erased random walk (the relation to the usual Markov property
is somewhat vague).
It is important to notice that while the proof of the equivalence is quite easy, normally models which involve dynamically changing harmonic functions or measures are extremely difficult to analyze. Practically nothing is known about the p-Laplacian walk or diffusion-limited aggregation
. Another somewhat related model is the harmonic explorer.
Finally there is another link that should be mentioned: Kirchhoff's theorem
relates the number of spanning trees of a graph G to the eigenvalues of the discrete Laplacian. See spanning tree
for details.
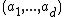with integer 
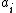. This is an infinite graph with degree 2d when you connect each point to its nearest neighbors. From now on we will consider loop-erased random walk on this graph or its subgraphs.
as n goes to infinity. Dimension 4 is more complicated, but the general picture is still true. It turns out that the loop-erasure of a random walk of length n has approximately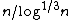
vertices, but again, after scaling (that takes into account the logarithmic factor) the loop-erased walk converges to Brownian motion.
and simulation results led to a number of exciting conjectures. Assume D is some simply connected domain
in the plane and x is a point in D. Take the graph G to be
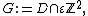
that is, a grid of side length ε restricted to D. Let v be the vertex of G closest to x. Examine now a loop-erased random walk starting from v and stopped when hitting the "boundary" of G, i.e. the vertices of G which correspond to the boundary of D. Then the conjectures are
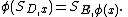
The first attack at these conjectures came from the direction of domino tiling
s. Taking a spanning tree of G and adding to it its planar dual
one gets a domino
tiling of a special derived graph (call it H). Each vertex of H corresponds to a vertex, edge or face of G, and the edges of H show which vertex lies on which edge and which edge on which face. It turns out that taking a uniform spanning tree of G leads to a uniformly distributed random domino tiling of H. The number of domino tilings of a graph can be calculated using the determinant of special matrices, which allow to connect it to the discrete Green function
which is approximately conformally invariant. These arguments allowed to show that certain measurables of loop-erased random walk are (in the limit) conformally invariant, and that the expected
number of vertices in a loop-erased random walk stopped at a circle of radius r is of the order of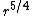
.
In 2002 these conjectures were resolved (positively) using Stochastic Löwner Evolution. Very roughly, it is a stochastic conformally invariant partial differential equation
which allows to catch the Markov property of loop-erased random walk (and many other probabilistic processes).
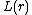denotes the expected number of vertices in the loop-erased random walk until it gets to a distance of r, then
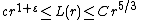
where ε, c and C are some positive numbers (the numbers can, in principle, be calculated from the proofs, but the authors did not do it). This suggests that the scaling limit should have Hausdorff dimension between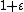
and 5/3 almost surely. Numerical experiments show that it should be 
.
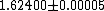Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, loop-erased random walk is a model for a random simple path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
with important applications in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and, in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. It is intimately connected to the uniform spanning tree, a model for a random tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
. See also random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
for more general treatment of this topic.
Definition
Assume G is some graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
and
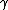is some pathPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
of length n on G. In other words,
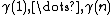are vertices of G such that 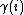and 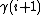are neighbors. Then the loop erasure of 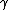is a new simple path created by erasing all the loops of 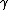in chronological order. Formally, we define indices 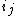inductivelyMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
using
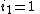
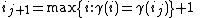
where "max" here means up to the length of the path
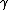. The induction stops when for some 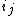we have 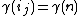. Assume this happens at J i.e. 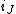is the last 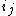. Then the loop erasure of 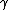, denoted by 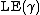is a simple path of length J defined by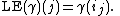Now let G be some graph, let v be a vertex of G, and let R be a random walk on G starting from v. Let T be some stopping time for R. Then the loop-erased random walk until time T is LE(R([1,T])). In other words, take R from its beginning until T — that's a (random) path — erase all the loops in chronological order as above — you get a random simple path.
The stopping time T may be fixed, i.e. one may perform n steps and then loop-erase. However, it is usually more natural to take T to be the hitting time
Hitting time
In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
in some set. For example, let G be the graph Z2 and let R be a random walk starting from the point (0,0). Let T be the time when R first hits the circle of radius 100 (we mean here of course a discretized circle). LE(R) is called the loop-erased random walk starting at (0,0) and stopped at the circle.
The uniform spanning tree
Let G again be a graph. A spanning treeSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of G is a subgraph of G containing all vertices and some of the edges, which is a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, i.e. connected and with no cycles. The uniform spanning tree (UST for short) is a random spanning tree chosen among all the possible spanning trees of G with equal probability.
Let now v and w be two vertices in G. Any spanning tree contains precisely one simple path between v and w. Taking this path in the uniform spanning tree gives a random simple path. It turns out that the distribution of this path is identical to the distribution of the loop-erased random walk starting at v and stopped at w.
An immediate corollary is that loop-erased random walk is symmetric in its start and end points. More precisely, the distribution of the loop-erased random walk starting at v and stopped at w is identical to the distribution of the reversal of loop-erased random walk starting at w and stopped at v. This is not a trivial fact at all! Loop-erasing a path and the reverse path do not give the same result. It is only the distributions that are identical.
A-priori sampling
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
a UST seems difficult. Even a relatively modest graph (say a 100x100 grid) has way too many spanning trees to prepare a complete list. Therefore a different approach is needed. There are a number of algorithms for sampling a UST, but we will concentrate on Wilson's algorithm.
Take any two vertices and perform loop-erased random walk from one to the other. Now take a third vertex (not on the constructed path) and perform loop-erased random walk until hitting the already constructed path. This gives a tree with three leaves. Choose a fourth vertex and do loop-erased random walk until hitting this tree. Continue until the tree spans all the vertices. It turns out that no matter which method you use to choose the starting vertices you always end up with the same distribution on the spanning trees, namely the uniform one.
The Laplacian random walk
Another representation of loop-erased random walk stems from solutions of the discreteDiscrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
Laplace equation. Let again G be a graph and let v and w be two vertices in G. Construct a random path from v to w inductively using the following procedure. Assume we have already defined
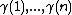. Let f be a function from G to R satisfying 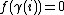for all 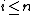and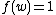
- f is discretely harmonicHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
everywhere else
Where a function f on a graph is discretely harmonic at a point x if f(x) equals the average of f on the neighbors of x.
With f defined choose
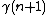using f at the neighbors of 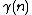as weights. In other words, if 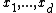are these neighbors, choose 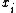with probability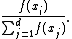Continue this process, (notice that at each step you have to calculate f again) and you will end up with a random simple path from v to w. It turns out that the distribution of this path is identical to that of a loop-erased random walk from v to w.
An alternative view is that the distribution of a loop-erased random walk conditioned
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
to start in some path β is identical to the loop-erasure of a random walk conditioned not to hit β. This property is often referred to as the Markov property of loop-erased random walk (the relation to the usual Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
is somewhat vague).
It is important to notice that while the proof of the equivalence is quite easy, normally models which involve dynamically changing harmonic functions or measures are extremely difficult to analyze. Practically nothing is known about the p-Laplacian walk or diffusion-limited aggregation
Brownian tree
A Brownian tree, whose name is derived from Robert Brown via Brownian motion, is a form of computer art that was briefly popular in the 1990s, when home computers started to have sufficient power to simulate Brownian motion...
. Another somewhat related model is the harmonic explorer.
Finally there is another link that should be mentioned: Kirchhoff's theorem
Kirchhoff's theorem
In the mathematical field of graph theory Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph...
relates the number of spanning trees of a graph G to the eigenvalues of the discrete Laplacian. See spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
for details.
Grids
Let d be the dimension, which we will assume to be at least 2. Examine Zd i.e. all the points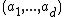 with integer 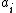. This is an infinite graph with degree 2d when you connect each point to its nearest neighbors. From now on we will consider loop-erased random walk on this graph or its subgraphs.High dimensions
The easiest case to analyze is dimension 5 and above. In this case it turns out that there the intersections are only local. A calculation shows that if one takes a random walk of length n, its loop-erasure has length of the same order of magnitude, i.e. n. Scaling accordingly, it turns out that loop-erased random walk converges (in an appropriate sense) to Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
as n goes to infinity. Dimension 4 is more complicated, but the general picture is still true. It turns out that the loop-erasure of a random walk of length n has approximately
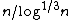vertices, but again, after scaling (that takes into account the logarithmic factor) the loop-erased walk converges to Brownian motion.Two dimensions
In two dimensions, arguments from conformal field theoryConformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and simulation results led to a number of exciting conjectures. Assume D is some simply connected domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
in the plane and x is a point in D. Take the graph G to be
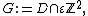
that is, a grid of side length ε restricted to D. Let v be the vertex of G closest to x. Examine now a loop-erased random walk starting from v and stopped when hitting the "boundary" of G, i.e. the vertices of G which correspond to the boundary of D. Then the conjectures are
- As ε goes to zero the distribution of the path converges to some distribution on simple paths from x to the boundary of D (different from Brownian motion, of course — in 2 dimensions paths of Brownian motion are not simple). This distribution (denote it by
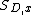) is called the scaling limit of loop-erased random walk. - These distributions are conformally invariantConformal mapIn mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
. Namely, if φ is a Riemann map between D and a second domain E then
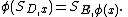
- The Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of these paths is 5/4 almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
.
The first attack at these conjectures came from the direction of domino tiling
Domino tiling
A domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge...
s. Taking a spanning tree of G and adding to it its planar dual
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
one gets a domino
Dominoes
Dominoes generally refers to the collective gaming pieces making up a domino set or to the subcategory of tile games played with domino pieces. In the area of mathematical tilings and polyominoes, the word domino often refers to any rectangle formed from joining two congruent squares edge to edge...
tiling of a special derived graph (call it H). Each vertex of H corresponds to a vertex, edge or face of G, and the edges of H show which vertex lies on which edge and which edge on which face. It turns out that taking a uniform spanning tree of G leads to a uniformly distributed random domino tiling of H. The number of domino tilings of a graph can be calculated using the determinant of special matrices, which allow to connect it to the discrete Green function
Green function
Green function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
which is approximately conformally invariant. These arguments allowed to show that certain measurables of loop-erased random walk are (in the limit) conformally invariant, and that the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
number of vertices in a loop-erased random walk stopped at a circle of radius r is of the order of
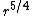.In 2002 these conjectures were resolved (positively) using Stochastic Löwner Evolution. Very roughly, it is a stochastic conformally invariant partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
which allows to catch the Markov property of loop-erased random walk (and many other probabilistic processes).
Three dimensions
The scaling limit exists and is invariant under rotations and dilations. If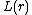 denotes the expected number of vertices in the loop-erased random walk until it gets to a distance of r, then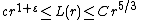where ε, c and C are some positive numbers (the numbers can, in principle, be calculated from the proofs, but the authors did not do it). This suggests that the scaling limit should have Hausdorff dimension between
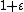and 5/3 almost surely. Numerical experiments show that it should be .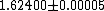