List of cohomology theories
Encyclopedia
This is a list of some of the ordinary and generalized (or extraordinary) homology and cohomology theories in algebraic topology
that are defined on the categories of CW complex
es or spectra
. For other sorts of homology theories see the links at the end of this article.
If X is a spectrum, then it defines generalized homology and cohomology theories on the category of spectra as follows.
that the homology of a point vanishes in dimension other than 0. They are determined by an abelian
coefficient group G, and denoted by H(X, G) (where
G is sometimes omitted, especially if it is Z). Usually G is the integers, the rationals, the reals, the complex numbers, or the integers mod a prime p.
The cohomology functors of ordinary cohomology theories are represented by Eilenberg-MacLane space
s.
On simplicial complexes, these theories coincide with singular homology
and cohomology.
Coefficient ring: πn(H) = Z if n=0, 0 otherwise.
The original homology theory.
Coefficient ring: πn(HQ) = Q if n=0, 0 otherwise.
These are the easiest of all homology theories.
The homology groups HQn(X) are often denoted by Hn(X, Q).
The homology groups H(X, Q), H(X, R), H(X, C) with rational
, real
, and complex
coefficients are all similar, and are used mainly when torsion is not of interest (or too complicated to work out). The Hodge decomposition writes the complex cohomology of a complex projective variety as a sum of sheaf cohomology
groups.
Coefficient ring: πn(HZp) = Zp (Integers mod p) if n=0, 0 otherwise.
of a space are often related to vector bundle
s over the space, and different sorts of K-theories correspond to different structures that can be put on a vector bundle.
Coefficient ring: The coefficient groups πi(KO) have period 8 in i, given by the sequence Z, Z2, Z2,0, Z, 0, 0, 0, repeated. As a ring, it is generated by a class η in degree 1, a class x4 in degree 4, and an invertible class v14 in degree 8, subject to the relations that 2η=η3=ηx4=0, and x42=4v14.
KO0(X) is the ring of stable equivalence classes of real vector bundles over X. Bott periodicity implies that the K-groups have period 8.
Coefficient ring: The coefficient ring K*(point) is the ring of formal Laurent series in a generator of degree 2.
K0(X) is the ring of stable equivalence classes of complex vector bundles over X. Bott periodicity implies that the K-groups have period 2.
Coefficient ring: The coefficient groups πi(KSp) have period 8 in i, given by the sequence Z, 0, 0, 0,Z, Z2, Z2,0, repeated.
KSp0(X) is the ring of stable equivalence classes of quaternionic vector bundles over X. Bott periodicity implies that the K-groups have period 8.
G is some abelian group; for example the localization Z(p) at the prime p. Other K-theories can also be given coefficients.
Coefficient ring: to be written...
The coefficient groups πi(KSC) have period 4 in i, given by the sequence Z, Z2, 0, Z, repeated. Introduced by D. Anderson in his unpublished 1964 Berkeley PhD dissertation, "A new cohomology theory".
Coefficient ring: For ku, the coefficient ring is the ring of polynomials over Z on a single class v1 in dimension 2. For ko, the coefficient ring is the quotient of a polynomial ring on three generators, η in dimension 1, x4 in dimension 4, and v14 in dimension 8, the periodicity generator, modulo the relations that 2η=0, x4²=4v14, η³=0, and ηx=0.
Roughly speaking, this is K-theory with the negative dimensional parts killed off.
studies manifold
s, where a manifold is regarded as "trivial" if it is the boundary of another compact manifold. The cobordism classes of manifolds form a ring that is usually the coefficient ring of some generalized cohomology theory. There are many such theories, corresponding roughly to the different structures that one can put on a manifold.
The functors of cobordism theories are often represented by Thom space
s of certain groups.
Stable homotopy
Spectrum: S (sphere spectrum
).
Coefficient ring: The coefficient groups πn(S) are the stable homotopy groups of spheres, which are notoriously hard to compute or understand for n>0.
(For n<0 they vanish, and for n=0 the group is Z.)
Stable homotopy is closely related to cobordism of framed manifolds (manifolds with a trivialization of the normal bundle).
)
Coefficient ring: π*(MO) is the ring of cobordism classes of unoriented manifolds, and is a polynomial ring over the field with 2 elements on generators of degree i for every i not of the form 2n−1.
Unoriented bordism is 2-torsion, since 2M is the boundary of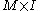
.
MO is a rather weak cobordism theory, as the spectrum MO is isomorphic to
H(π*(MO)) ("homology with coefficients in π*(MO)") – MO is a product of Eilenberg-MacLane spectra. In other words the corresponding homology and cohomology theories are no more powerful than homology and cohomology with coefficients in Z/2Z. This was the first cobordism theory to be described completely.
)
Coefficient ring: π*(MU) is the polynomial ring on generators of degree 2, 4, 6, 8, ...
and is naturally isomorphic to Lazard's universal ring, and is the cobordism ring of stably almost complex manifold
s.
Coefficient ring: The oriented cobordism class of a manifold is completely determined by its characteristic numbers: its Stiefel-Whitney numbers and Pontryagin numbers, but the overall coefficient ring, denoted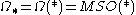
is quite complicated.
Rationally, and at 2 (corresponding to Pontryagin and Stiefel-Whitney classes, respectively), MSO is a product of Eilenberg-MacLane spectra –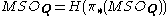
and 
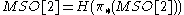– but at odd primes it is not, and the structure is complicated to described. The ring has been completely described integrally, due to work of Milnor, Averbuch, Rokhlin, and C.T.C. Wall.
)
Coefficient ring:
Coefficient ring: See .
)
Coefficient ring:
Coefficient ring:
The definition is similar to cobordism, except that one uses piecewise linear or topological instead of smooth manifold
s, either oriented or unoriented.
The coefficient rings are complicated.
Coefficient ring: π*(BP) is a polynomial algebra over Z(p) on generators vn of dimension 2(pn−1) for n≥1.
Brown–Peterson cohomology BP is a summand of MUp, which is complex cobordism MU localized at a prime p. In fact MU(p) is a sum of suspensions of BP.
Coefficient ring: Fp[vn, vn−1], where vn has degree 2(pn−1).
These theories have period 2(pn−1). Named for Jack Morava
.
Coefficient ring Z(2)[v1, ...,vn, 1/vn] where vi has degree 2(2i−1)
The coefficient ring π*(tmf) is called the ring of topological modular forms
. TMF is tmf with the 24th power of the modular form Δ inverted, and has period 242=576. At the prime p=2, the completion of tmf is the spectrum eo2, and the K(2)-localization of tmf is the Hopkins-Miller Higher Real K-theory spectrum EO2.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
that are defined on the categories of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es or spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
. For other sorts of homology theories see the links at the end of this article.
Notation
- S = π = S0 is the sphere spectrum.
- Sn is the spectrum of the n-dimensional sphere
- SnY = Sn∧Y is the nth suspension of a spectrum Y.
- [X,Y] is the abelian group of morphisms from the spectrum X to the spectrum Y, given (roughly) as homotopy classes of maps.
- [X,Y]n = [SnX,Y]
- [X,Y]* is the graded abelian group given as the sum of the groups [X,Y]n.
- πn(X) = [Sn, X] = [S, X]n is the nth stable homotopy group of X.
- π*(X) is the sum of the groups πn(X), and is called the coefficient ring of X when X is a ring spectrum.
- X∧Y is the smash productSmash productIn mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
of two spectra.
If X is a spectrum, then it defines generalized homology and cohomology theories on the category of spectra as follows.
- Xn(Y) = [S, X∧Y]n = [Sn, X∧Y] is the generalized homology of Y,
- Xn(Y) = [Y, X]−n = [S−nY, X] is the generalized cohomology of Y
Ordinary homology theories
These are the theories satisfying the "dimension axiom" of the Eilenberg-Steenrod axiomsEilenberg-Steenrod axioms
In mathematics, specifically in algebraic topology, the Eilenberg–Steenrod axioms are properties that homology theories of topological spaces have in common...
that the homology of a point vanishes in dimension other than 0. They are determined by an abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
coefficient group G, and denoted by H(X, G) (where
G is sometimes omitted, especially if it is Z). Usually G is the integers, the rationals, the reals, the complex numbers, or the integers mod a prime p.
The cohomology functors of ordinary cohomology theories are represented by Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
s.
On simplicial complexes, these theories coincide with singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and cohomology.
Homology and cohomology with integer coefficients.
Spectrum: H (Eilenberg-MacLane spectrum of the integers.)Coefficient ring: πn(H) = Z if n=0, 0 otherwise.
The original homology theory.
Homology and cohomology with rational (or real or complex) coefficients.
Spectrum: HQ (Eilenberg-Mac Lane spectrum of the rationals.)Coefficient ring: πn(HQ) = Q if n=0, 0 otherwise.
These are the easiest of all homology theories.
The homology groups HQn(X) are often denoted by Hn(X, Q).
The homology groups H(X, Q), H(X, R), H(X, C) with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, and complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients are all similar, and are used mainly when torsion is not of interest (or too complicated to work out). The Hodge decomposition writes the complex cohomology of a complex projective variety as a sum of sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
groups.
Homology and cohomology with mod p coefficients.
Spectrum: HZp (Eilenberg-Maclane spectrum of the integers mod p.)Coefficient ring: πn(HZp) = Zp (Integers mod p) if n=0, 0 otherwise.
K-theories
The simpler K-theoriesK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
of a space are often related to vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over the space, and different sorts of K-theories correspond to different structures that can be put on a vector bundle.
Real K-theory
Spectrum: KOCoefficient ring: The coefficient groups πi(KO) have period 8 in i, given by the sequence Z, Z2, Z2,0, Z, 0, 0, 0, repeated. As a ring, it is generated by a class η in degree 1, a class x4 in degree 4, and an invertible class v14 in degree 8, subject to the relations that 2η=η3=ηx4=0, and x42=4v14.
KO0(X) is the ring of stable equivalence classes of real vector bundles over X. Bott periodicity implies that the K-groups have period 8.
Complex K-theory
Spectrum: KU (even terms BU or Z× BU, odd terms U).Coefficient ring: The coefficient ring K*(point) is the ring of formal Laurent series in a generator of degree 2.
K0(X) is the ring of stable equivalence classes of complex vector bundles over X. Bott periodicity implies that the K-groups have period 2.
Quaternionic K-theory
Spectrum: KSpCoefficient ring: The coefficient groups πi(KSp) have period 8 in i, given by the sequence Z, 0, 0, 0,Z, Z2, Z2,0, repeated.
KSp0(X) is the ring of stable equivalence classes of quaternionic vector bundles over X. Bott periodicity implies that the K-groups have period 8.
K theory with coefficients
Spectrum: KGG is some abelian group; for example the localization Z(p) at the prime p. Other K-theories can also be given coefficients.
Self conjugate K-theory
Spectrum: KSCCoefficient ring: to be written...
The coefficient groups πi(KSC) have period 4 in i, given by the sequence Z, Z2, 0, Z, repeated. Introduced by D. Anderson in his unpublished 1964 Berkeley PhD dissertation, "A new cohomology theory".
Connective K-theories
Spectrum: ku for connective K-theory, ko for connective real K-theory.Coefficient ring: For ku, the coefficient ring is the ring of polynomials over Z on a single class v1 in dimension 2. For ko, the coefficient ring is the quotient of a polynomial ring on three generators, η in dimension 1, x4 in dimension 4, and v14 in dimension 8, the periodicity generator, modulo the relations that 2η=0, x4²=4v14, η³=0, and ηx=0.
Roughly speaking, this is K-theory with the negative dimensional parts killed off.
KR-theory
This is a cohomology theory defined for spaces with involution, from which many of the other K-theories can be derived.Bordism and cobordism theories
CobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
studies manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, where a manifold is regarded as "trivial" if it is the boundary of another compact manifold. The cobordism classes of manifolds form a ring that is usually the coefficient ring of some generalized cohomology theory. There are many such theories, corresponding roughly to the different structures that one can put on a manifold.
The functors of cobordism theories are often represented by Thom space
Thom space
In mathematics, the Thom space, Thom complex, or Pontryagin-Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space....
s of certain groups.
Stable homotopyStable homotopy theoryIn mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
and cohomotopy
Spectrum: S (sphere spectrumSphere spectrum
In stable homotopy theory, a branch of mathematics, the sphere spectrum S is the smallest nontrivial spectrum. It is the suspension spectrum of S0, i.e., a set of two points. Explicitly, the nth space in the sphere spectrum is the n-dimensional sphere Sn, and the structure maps from the suspension...
).
Coefficient ring: The coefficient groups πn(S) are the stable homotopy groups of spheres, which are notoriously hard to compute or understand for n>0.
(For n<0 they vanish, and for n=0 the group is Z.)
Stable homotopy is closely related to cobordism of framed manifolds (manifolds with a trivialization of the normal bundle).
Unoriented cobordism
Spectrum: MO (Thom spectrum of orthogonal groupOrthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
)
Coefficient ring: π*(MO) is the ring of cobordism classes of unoriented manifolds, and is a polynomial ring over the field with 2 elements on generators of degree i for every i not of the form 2n−1.
Unoriented bordism is 2-torsion, since 2M is the boundary of
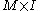.MO is a rather weak cobordism theory, as the spectrum MO is isomorphic to
H(π*(MO)) ("homology with coefficients in π*(MO)") – MO is a product of Eilenberg-MacLane spectra. In other words the corresponding homology and cohomology theories are no more powerful than homology and cohomology with coefficients in Z/2Z. This was the first cobordism theory to be described completely.
Complex cobordism
Spectrum: MU (Thom spectrum of unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
)
Coefficient ring: π*(MU) is the polynomial ring on generators of degree 2, 4, 6, 8, ...
and is naturally isomorphic to Lazard's universal ring, and is the cobordism ring of stably almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
s.
Oriented cobordism
Spectrum: MSO (Thom spectrum of special orthogonal group)Coefficient ring: The oriented cobordism class of a manifold is completely determined by its characteristic numbers: its Stiefel-Whitney numbers and Pontryagin numbers, but the overall coefficient ring, denoted
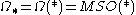is quite complicated.Rationally, and at 2 (corresponding to Pontryagin and Stiefel-Whitney classes, respectively), MSO is a product of Eilenberg-MacLane spectra –
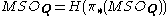and 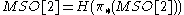– but at odd primes it is not, and the structure is complicated to described. The ring has been completely described integrally, due to work of Milnor, Averbuch, Rokhlin, and C.T.C. Wall.Special unitary cobordism
Spectrum: MSU (Thom spectrum of special unitary groupSpecial unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
)
Coefficient ring:
Spin cobordism (and variants)
Spectrum: MSpin (Thom spectrum of spin group)Coefficient ring: See .
Symplectic cobordism
Spectrum: MSp (Thom spectrum of symplectic groupSymplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
)
Coefficient ring:
PL cobordism and topological cobordism
Spectrum: MPL, MSPL, MTop, MSTopCoefficient ring:
The definition is similar to cobordism, except that one uses piecewise linear or topological instead of smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, either oriented or unoriented.
The coefficient rings are complicated.
Brown–Peterson cohomology
Spectrum: BPCoefficient ring: π*(BP) is a polynomial algebra over Z(p) on generators vn of dimension 2(pn−1) for n≥1.
Brown–Peterson cohomology BP is a summand of MUp, which is complex cobordism MU localized at a prime p. In fact MU(p) is a sum of suspensions of BP.
Morava K-theory
Spectrum: K(n) (They also depend on a prime p.)Coefficient ring: Fp[vn, vn−1], where vn has degree 2(pn−1).
These theories have period 2(pn−1). Named for Jack Morava
Jack Morava
Jack Johnson Morava is an American topologist.Of Czech and Appalachian descent, he was raised in Mercedes, Texas ; an early interest in topology was strongly encouraged by his parents...
.
Johnson–Wilson theory
Spectrum E(n)Coefficient ring Z(2)[v1, ...,vn, 1/vn] where vi has degree 2(2i−1)
Topological modular forms
Spectra: tmf, TMF (previously called eo2.)The coefficient ring π*(tmf) is called the ring of topological modular forms
Topological modular forms
In mathematics, the spectrum of topological modular forms describes a generalized cohomology theory whose coefficient ring is related to the graded ring of holomorphic modular forms with integral cusp expansions...
. TMF is tmf with the 24th power of the modular form Δ inverted, and has period 242=576. At the prime p=2, the completion of tmf is the spectrum eo2, and the K(2)-localization of tmf is the Hopkins-Miller Higher Real K-theory spectrum EO2.