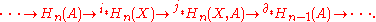Eilenberg-Steenrod axioms
Encyclopedia
In mathematics
, specifically in algebraic topology
, the Eilenberg–Steenrod axioms are properties that homology theories
of topological space
s have in common. The quintessential example of a homology theory satisfying the axioms is singular homology
, developed by Samuel Eilenberg
and Norman Steenrod
.
Indeed, one can define a homology theory as a sequence
of functor
s satisfying the Eilenberg–Steenrod axioms. The axiomatic approach, which was developed in 1945, allows one to prove results, such as the Mayer–Vietoris sequence, that are common to all homology theories satisfying the axioms.
If one omits the dimension axiom (described below), then the remaining axioms define what is called an extraordinary homology theory. Extraordinary cohomology theories first arose in K-theory
and cobordism.
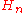 from the category
from the category
of pairs
(X, A) of topological spaces to the category of abelian group
s, together with a natural transformation
 called the boundary map (here Hi − 1(A) is a shorthand for Hi − 1(A,∅)). The axioms are:
called the boundary map (here Hi − 1(A) is a shorthand for Hi − 1(A,∅)). The axioms are:
If P is the one point space then H0(P) is called the coefficient group. For example, singular homology (taken with integer coefficients, as is most common) has as coefficients the integers.
The homology of some relatively simple spaces, such as n-sphere
s, can be calculated directly from the axioms. From this it can be easily shown that the (n − 1)-sphere is not a retract of the n-disk. This is used in the proof of the Brouwer fixed point theorem
.
and cobordism theory, which are extraordinary cohomology theories, and come with homology theories dual to them.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Eilenberg–Steenrod axioms are properties that homology theories
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s have in common. The quintessential example of a homology theory satisfying the axioms is singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, developed by Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
.
Indeed, one can define a homology theory as a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s satisfying the Eilenberg–Steenrod axioms. The axiomatic approach, which was developed in 1945, allows one to prove results, such as the Mayer–Vietoris sequence, that are common to all homology theories satisfying the axioms.
If one omits the dimension axiom (described below), then the remaining axioms define what is called an extraordinary homology theory. Extraordinary cohomology theories first arose in K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
and cobordism.
Formal definition
The Eilenberg–Steenrod axioms apply to a sequence of functors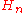 from the category
from the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of pairs
Topological pair
In mathematics, more specifically algebraic topology, a pair is short-hand for an inclusion of topological spaces i\colon A\hookrightarrow X. Sometimes i is assumed to be a cofibration...
(X, A) of topological spaces to the category of abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, together with a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
 called the boundary map (here Hi − 1(A) is a shorthand for Hi − 1(A,∅)). The axioms are:
called the boundary map (here Hi − 1(A) is a shorthand for Hi − 1(A,∅)). The axioms are:- Homotopy: Homotopic maps induce the same map in homology. That is, if
 is homotopic to
is homotopic to 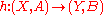 , then their induced mapsMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
, then their induced mapsMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
are the same. - ExcisionExcision theoremIn algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
: If (X, A) is a pair and U is a subset of X such that the closure of U is contained in the interior of A, then the inclusion map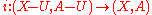 induces an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
induces an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
in homology. - Dimension: Let P be the one-point space; then
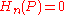 for all
for all  .
. - Additivity: If
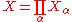 , the disjoint union of a family of topological spaces
, the disjoint union of a family of topological spaces 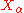 , then
, then 
- Exactness: Each pair (X, A) induces a long exact sequence in homology, via the inclusions
 and
and 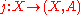 :
:
If P is the one point space then H0(P) is called the coefficient group. For example, singular homology (taken with integer coefficients, as is most common) has as coefficients the integers.
Consequences
Some facts about homology groups can be derived directly from the axioms, such as the fact that homotopically equivalent spaces have isomorphic homology groups.The homology of some relatively simple spaces, such as n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, can be calculated directly from the axioms. From this it can be easily shown that the (n − 1)-sphere is not a retract of the n-disk. This is used in the proof of the Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
.
Dimension axiom
A "homology-like" theory satisfying all of the Eilenberg–Steenrod axioms except the dimension axiom is called an extraordinary homology theory (dually, extraordinary cohomology theory). Important examples of these were found in the 1950s, such as topological K-theoryTopological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
and cobordism theory, which are extraordinary cohomology theories, and come with homology theories dual to them.