Piecewise linear - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a piecewise linear function is a piecewise

Piecewise

On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...

-defined function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

whose pieces are linear

Linear function

In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....

Examples

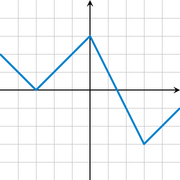
The function defined by:

is piecewise linear with four pieces. (The graph of this function is shown to the right.) Since the graph of a linear function is a line

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

, the graph of a piecewise linear function consists of line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

s and rays. If the function is continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

, the graph will be a polygonal curve. In simple piece wise linear function means line fitting with reference to different points.

Other examples of piecewise linear functions include the absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

function, the square wave

Square wave

A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...

, the sawtooth function, and the floor function

Floor function

In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...

Notation

The notion of a piecewise linear function makes sense in several different contexts. Piecewise linear functions may be defined on n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, or more generally any vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

or affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

, as well as on piecewise linear manifold

Piecewise linear manifold

In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...

s, simplicial complex

Simplicial complex

In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...

es, and so forth. In each case, the function may be real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued, or it may take values from a vector space, an affine space, a piecewise-linear manifold, or a simplicial complex. (In these contexts, the term “linear” does not refer solely to linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

s, but to more general affine linear

Affine transformation

In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...

functions.)

In dimensions higher than one, it is common to require the domain of each piece to be a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

or polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

. This guarantees that the graph of the function will be composed of polygonal or polytopal pieces.

Important sub-classes of piecewise linear functions include the continuous

Continuous function

piecewise linear functions and the convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

piecewise linear functions. Splines

Spline (mathematics)

In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...

generalize piecewise linear functions to higher-order polynomials, and more one can speak of piecewise-differentiable functions, as in PDIFF

PDIFF

In geometric topology, PDIFF, for piecewise differentiable, is the category of piecewise-smooth manifolds and piecewise-smooth maps between them...

Examples

Notation

See also