Bounded mean oscillation
Encyclopedia
In harmonic analysis
, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded (finite). The space of functions of bounded mean oscillation (BMO), is a function space
that, in some precise sense, plays the same role in the theory of Hardy space
s Hp that the space L∞ of essentially bounded functions plays in the theory of Lp-spaces
: it is also called John–Nirenberg space, after Fritz John
and Louis Nirenberg
who introduced and studied it for the first time.
from a bounded set
belonging to ℝn into ℝn and the corresponding problems arising from elasticity theory
, precisely from the concept of elastic strain: the basic notation was introduced in a closely following paper by , where several properties of this function spaces were proved. The next important step in the development of the theory was the proof by Charles Fefferman
of the duality
between BMO and the Hardy space
H1, in the noted paper : a constructive proof of this result, introducing new methods and starting a further development of the theory, was given by Akihito Uchiyama.
u (i.e. a function belonging to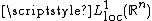
) over a hypercube
Q in ℝn is defined as the following integral
:
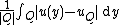
where
A BMO function is any function u belonging to
whose mean oscillation has a finite supremum
over the set of all cube
s Q contained in ℝn.
Note. The use of cube
s Q in ℝn as the integration domains on which the is calculated, is not mandatory: uses balls
instead and, as remarked by , in doing so a perfectly equivalent of definition of functions
of bounded mean oscillation arises.
by the constant function
s (which have BMO norm 0).
such that their boundaries touch and the sidelength of Q is no less than one-half the sidelength of R, then
where C>0 is some universal constant. This property is, in fact, equivalent to f being in BMO, that is, if f is a locally integrable function such that |fR-fQ|≤C for all dyadic cubes Q and R adjacent in the sense described above, then f is in BMO and its BMO norm is proportional to the constant C.
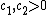such that whenever 
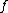∈ BMO(ℝn), then for any cube Q in ℝn,
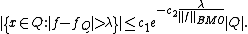
Conversely, if this inequality holds over all cube
s with some constant C in place of ||f||BMO, then f is in BMO with norm at most a constant times C.
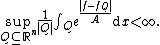
The John–Nirenberg inequality implies that A(f)≤C||f||BMO for some universal constant C. For an L∞ function, however, the above inequality will hold for all A>0. In other words, A(f)=0 if f is in L∞. Hence the constant A(f) gives us a way of measuring how far a function in BMO is from the subspace L∞. This statement can be made more precise: there is a constant C, depending only on the dimension n, such that for any function
∈ BMO(ℝn) the following two-sided inequality holds
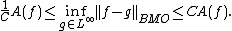
of harmonic function
s on the unit disk and plays a major role in the theory of Hardy spaces: by using , it is possible to define the BMO(T) space on the unit circle
as the space of functions
such that
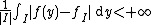
i.e. such that its over every arc I of the unit circle
is bounded. Here as before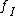
is the mean value of f over the arc I.
An Analytic function on the unit disk is said to belong to the Harmonic BMO or in the BMOH space if and only if it is the Poisson integral of a BMO(T) function. Therefore BMOH is the space of all functions u with the form:
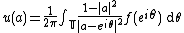
equipped with the norm:
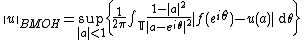
The subspace of analytic functions belonging BMOH is called the Analytic BMO space or the BMOA space.
in his original paper proved that the real BMO space is dual to the real valued harmonic Hardy space on the upper half-space
ℝn×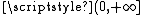
. Today in the theory of Complex and Harmonic analysis the following - modern - approach for analytic functions, is more often considered. Let 
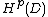be the Analytic Hardy space
on the unit Disc. For p = 1 we identify (H1)* with BMOA by pairing f ∈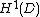
and g ∈ BMOA using the anti-linear transformation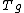 
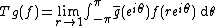
Notice that although the limit always exists for an H1 function f and
is an element of the dual space (H1)*, since the transformation is anti-linear, we don't have an isometric isomorphism between (H1)* and BMOA. However one can obtain an isometry if they consider a kind of space of conjugate BMOA functions.
in ℝn. The space dyadic BMO, written BMOd is the space of functions satisfying the same inequality as for BMO functions, only that the supremum is over all dyadic cubes. This supremum is sometimes denoted ||•||BMOd.
This space is contained in but still distinct from BMO as it depends greatly on the position of the dyadic cubes. In particular, the function log(x)χ[0,∞) is a function that is in dyadic BMO but not in BMO. However, if a function f is such that ||f(•-x)||BMOd≤C for all x in ℝn for some C>0, then by the one-third trick f is also in BMO.
Although dyadic BMO is a much narrower class than BMO, many theorems that are true for BMO are much simpler to prove for dyadic BMO, and in some cases one can recover the original BMO theorems by proving them first in the special dyadic case.
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded (finite). The space of functions of bounded mean oscillation (BMO), is a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
that, in some precise sense, plays the same role in the theory of Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s Hp that the space L∞ of essentially bounded functions plays in the theory of Lp-spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
: it is also called John–Nirenberg space, after Fritz John
Fritz John
Fritz John was a German-born mathematician specialising in partial differential equations and ill-posed problems. His early work was on the Radon transform and he is remembered for John's equation.-Biography:...
and Louis Nirenberg
Louis Nirenberg
Louis Nirenberg is a Canadian mathematician, and one of the outstanding analysts of the twentieth century. He has made fundamental contributions to linear and nonlinear partial differential equations and their application to complex analysis and geometry.He was born in Hamilton, Ontario and...
who introduced and studied it for the first time.
Historical note
According to , the space of functions of bounded mean oscillation was introduced by in connection with his studies of mappingsMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from a bounded set
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
belonging to ℝn into ℝn and the corresponding problems arising from elasticity theorySolid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
, precisely from the concept of elastic strain: the basic notation was introduced in a closely following paper by , where several properties of this function spaces were proved. The next important step in the development of the theory was the proof by Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
of the duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
between BMO and the Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H1, in the noted paper : a constructive proof of this result, introducing new methods and starting a further development of the theory, was given by Akihito Uchiyama.
Definition
The mean oscillation of a locally integrable functionLocally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
u (i.e. a function belonging to
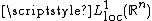) over a hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
Q in ℝn is defined as the following integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
:
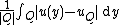
where
- |Q| is the volume of Q, i.e. its Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
- uQ is the average value of u on the cube Q, i.e.
-
.
A BMO function is any function u belonging to
whose mean oscillation has a finite supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
over the set of all cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s Q contained in ℝn.
Note. The use of cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s Q in ℝn as the integration domains on which the is calculated, is not mandatory: uses balls
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
instead and, as remarked by , in doing so a perfectly equivalent of definition of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of bounded mean oscillation arises.
BMO functions are locally p–integrable
BMO functions are locally Lp if 0 < p < ∞ , but need not be locally bounded.BMO is a Banach space
The supremum of the mean oscillation is called the BMO norm of u and is denoted by ||u||BMO (and in some instances it is also denoted ||u||*). The function ||u||BMO becomes a norm on BMO functions after quotienting outQuotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
by the constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
s (which have BMO norm 0).
Averages of adjacent cubes are comparable
As the name suggests, the mean or average of a function in BMO shouldn't oscillate very much when computing it over cubes close to each other in position and scale. To be more precise, if Q and R are dyadic cubesDyadic cubes
In mathematics, the dyadic cubes are a collection of cubes in ℝn of different sizes or scales such that the set of cubes of each scale partition ℝn and each cube in one scale may be written as a union of cubes of a smaller scale...
such that their boundaries touch and the sidelength of Q is no less than one-half the sidelength of R, then
where C>0 is some universal constant. This property is, in fact, equivalent to f being in BMO, that is, if f is a locally integrable function such that |fR-fQ|≤C for all dyadic cubes Q and R adjacent in the sense described above, then f is in BMO and its BMO norm is proportional to the constant C.
The John–Nirenberg Inequality
The John–Nirenberg Inequality is an estimate that governs how far a function of bounded mean oscillation may deviate from its average by a certain amount.Statement
There are constants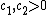 such that whenever 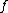∈ BMO(ℝn), then for any cube Q in ℝn,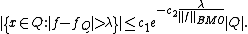Conversely, if this inequality holds over all cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s with some constant C in place of ||f||BMO, then f is in BMO with norm at most a constant times C.
A consequence: the distance in BMO to L∞
The John-Nirenberg inequality can actually give more information than just the BMO norm of a function. For a locally integrable function f, let A(f) be the infimal A>0 for which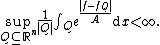The John–Nirenberg inequality implies that A(f)≤C||f||BMO for some universal constant C. For an L∞ function, however, the above inequality will hold for all A>0. In other words, A(f)=0 if f is in L∞. Hence the constant A(f) gives us a way of measuring how far a function in BMO is from the subspace L∞. This statement can be made more precise: there is a constant C, depending only on the dimension n, such that for any function
∈ BMO(ℝn) the following two-sided inequality holds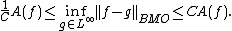The spaces BMOH and BMOA
When the dimension of the ambient space is 1, the space BMO can be seen as a subspaceSubspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s on the unit disk and plays a major role in the theory of Hardy spaces: by using , it is possible to define the BMO(T) space on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
as the space of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
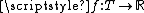such that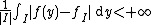i.e. such that its over every arc I of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is bounded. Here as before
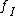is the mean value of f over the arc I.An Analytic function on the unit disk is said to belong to the Harmonic BMO or in the BMOH space if and only if it is the Poisson integral of a BMO(T) function. Therefore BMOH is the space of all functions u with the form:
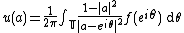
equipped with the norm:
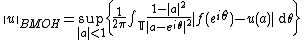
The subspace of analytic functions belonging BMOH is called the Analytic BMO space or the BMOA space.
BMOA as the dual space of H1(D)
Charles FeffermanCharles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
in his original paper proved that the real BMO space is dual to the real valued harmonic Hardy space on the upper half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
ℝn×
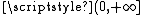. Today in the theory of Complex and Harmonic analysis the following - modern - approach for analytic functions, is more often considered. Let 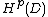be the Analytic Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
on the unit Disc. For p = 1 we identify (H1)* with BMOA by pairing f ∈
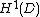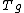
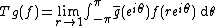
and g ∈ BMOA using the anti-linear transformation Notice that although the limit always exists for an H1 function f and
is an element of the dual space (H1)*, since the transformation is anti-linear, we don't have an isometric isomorphism between (H1)* and BMOA. However one can obtain an isometry if they consider a kind of space of conjugate BMOA functions.The space VMO
The space VMO of functions of vanishing mean oscillation is the closure in BMO of the continuous functions that vanish at infinity. It can also be defined as the space of functions whose "mean oscillations" on cubes Q are not only bounded, but also tend to zero uniformly as the radius of the cube Q tends to 0 or infinity. The space VMO is a sort of Hardy space analogue of the space of continuous functions vanishing at infinity, and in particular the real valued harmonic Hardy space H1 is the dual of VMO.The Dyadic BMO space
Let Δ denote the set of dyadic cubesDyadic cubes
In mathematics, the dyadic cubes are a collection of cubes in ℝn of different sizes or scales such that the set of cubes of each scale partition ℝn and each cube in one scale may be written as a union of cubes of a smaller scale...
in ℝn. The space dyadic BMO, written BMOd is the space of functions satisfying the same inequality as for BMO functions, only that the supremum is over all dyadic cubes. This supremum is sometimes denoted ||•||BMOd.
This space is contained in but still distinct from BMO as it depends greatly on the position of the dyadic cubes. In particular, the function log(x)χ[0,∞) is a function that is in dyadic BMO but not in BMO. However, if a function f is such that ||f(•-x)||BMOd≤C for all x in ℝn for some C>0, then by the one-third trick f is also in BMO.
Although dyadic BMO is a much narrower class than BMO, many theorems that are true for BMO are much simpler to prove for dyadic BMO, and in some cases one can recover the original BMO theorems by proving them first in the special dyadic case.
Examples
Examples of BMO functions include the following:- All bounded (measurable) functions. If f is in L∞, then ||f||BMO≤2||f||∞: however, the converse is not true as the following example shows.
- The function log(|P|) for any polynomial P that is not identically zero: in particular, this is true also for |P(x)|=|x|.
- If w is an A∞ weight, then log(w) is BMO. Conversely, if f is BMO, then eδf is an A∞ weight for δ>0 small enough: this fact is a consequence of the John-Nirenberg Inequality.