
Parabolic induction
Encyclopedia
In mathematics, parabolic induction is a method of constructing representation
s of a reductive group
from representations of its parabolic subgroups.
If G is a reductive algebraic group and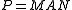 is the Langlands decomposition
is the Langlands decomposition
of a parabolic subgroup P, then parabolic induction consists of taking a representation of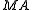 , extending it to P by letting N act trivially, and inducing
, extending it to P by letting N act trivially, and inducing
the result from P to G.
There are some generalizations of parabolic induction using cohomology
, such as cohomological parabolic induction and Deligne–Lusztig theory
.
, expressing his idea of a kind of reverse engineering of automorphic form
theory, from the point of view of representation theory
. The discrete group
Γ fundamental to the classical theory disappears, superficially. What remains is the basic idea that representations in general are to be constructed by parabolic induction of cuspidal representation
s. A similar philosophy was enunciated by Israel Gelfand
, and the philosophy is a precursor of the Langlands program
. A consequence for thinking about representation theory is that cuspidal representation
s are the fundamental class of objects, from which other representations may be constructed by procedures of induction.
According to Nolan Wallach
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s of a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
from representations of its parabolic subgroups.
If G is a reductive algebraic group and
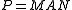 is the Langlands decomposition
is the Langlands decompositionLanglands decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product P=MAN of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.- Applications :...
of a parabolic subgroup P, then parabolic induction consists of taking a representation of
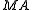 , extending it to P by letting N act trivially, and inducing
, extending it to P by letting N act trivially, and inducingInduced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
the result from P to G.
There are some generalizations of parabolic induction using cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
, such as cohomological parabolic induction and Deligne–Lusztig theory
Deligne–Lusztig theory
In mathematics, Deligne–Lusztig theory is a way of constructing linear representations of finite groups of Lie type using ℓ-adic cohomology with compact support, introduced by ....
.
Philosophy of cusp forms
The philosophy of cusp forms was a slogan of Harish-ChandraHarish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, expressing his idea of a kind of reverse engineering of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
theory, from the point of view of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. The discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
Γ fundamental to the classical theory disappears, superficially. What remains is the basic idea that representations in general are to be constructed by parabolic induction of cuspidal representation
Cuspidal representation
In number theory, cuspidal representations are certain representations of algebraic groups that occur discretely in L^2 spaces. The term cuspidal is derived, at a certain distance, from the cusp forms of classical modular form theory...
s. A similar philosophy was enunciated by Israel Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
, and the philosophy is a precursor of the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. A consequence for thinking about representation theory is that cuspidal representation
Cuspidal representation
In number theory, cuspidal representations are certain representations of algebraic groups that occur discretely in L^2 spaces. The term cuspidal is derived, at a certain distance, from the cusp forms of classical modular form theory...
s are the fundamental class of objects, from which other representations may be constructed by procedures of induction.
According to Nolan Wallach
Put in the simplest terms the "philosophy of cusp forms" says that for each Γ-conjugacy classes of Q-rational parabolic subgroups one should construct automorphic functions (from objects from spaces of lower dimensions) whose constant terms are zero for other conjugacy classes and the constant terms for [an] element of the given class give all constant terms for this parabolic subgroup. This is almost possible and leads to a description of all automorphic forms in terms of these constructs and cusp forms. The construction that does this is the Eisenstein seriesEisenstein seriesEisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
.

