
Solvable Lie algebra
Encyclopedia
In mathematics
, a Lie algebra
g is solvable if its derived series terminates in the zero subalgebra. That is, writing
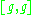
for the derived Lie algebra of g, generated by the set of values
for x and y in g, the derived series

becomes constant eventually at 0.
Any nilpotent Lie algebra is solvable, a fortiori, but the converse is not true. The solvable Lie algebras and the semisimple Lie algebras form two large and generally complementary classes, as is shown by the Levi decomposition
.
A maximal solvable subalgebra is called a Borel subalgebra. The largest solvable ideal is called the radical.
 be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
Lie's Theorem states that if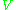 is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and
is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and  is a solvable linear Lie algebra over
is a solvable linear Lie algebra over 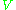 , then there exists a basis of
, then there exists a basis of 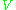 relative to which the matrices of all elements of
relative to which the matrices of all elements of 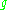 are upper triangular.
are upper triangular.
s of abstract group theory
. There are several possible definitions of solvable Lie group. For a Lie group
G, there is
To have equivalence one needs to assume G connected. For connected Lie groups, these definitions are the same, and the derived series of Lie algebras are the Lie algebra of the derived series of (closed) subgroups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
g is solvable if its derived series terminates in the zero subalgebra. That is, writing
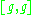
for the derived Lie algebra of g, generated by the set of values
- [x,y]
for x and y in g, the derived series

becomes constant eventually at 0.
Any nilpotent Lie algebra is solvable, a fortiori, but the converse is not true. The solvable Lie algebras and the semisimple Lie algebras form two large and generally complementary classes, as is shown by the Levi decomposition
Levi decomposition
In Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra....
.
A maximal solvable subalgebra is called a Borel subalgebra. The largest solvable ideal is called the radical.
Properties
Let be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
- (i)
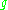 is solvable.
is solvable. - (ii)
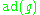 , the adjoint representation of
, the adjoint representation of 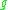 , is solvable.
, is solvable. - (iii) There is a finite sequence of ideals
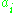 of
of 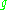 such that:
such that:
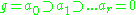 where
where 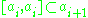 for all
for all 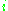 .
.
- (iv)
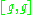 is nilpotent.
is nilpotent.
Lie's Theorem states that if
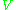 is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and
is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and  is a solvable linear Lie algebra over
is a solvable linear Lie algebra over 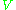 , then there exists a basis of
, then there exists a basis of 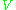 relative to which the matrices of all elements of
relative to which the matrices of all elements of 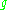 are upper triangular.
are upper triangular.Example
- Every abelian Lie algebra is solvable.
- Every nilpotent Lie algebra is solvable.
- Every Lie subalgebra, quotient and extension of a solvable Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is solvable. - Let
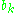 be a subalgebra of
be a subalgebra of 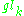 consisting of upper triangular matrices. Then
consisting of upper triangular matrices. Then 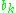 is solvable.
is solvable.
Solvable Lie groups
The terminology arises from the solvable groupSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s of abstract group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. There are several possible definitions of solvable Lie group. For a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G, there is
- termination of the usual derived series, in other words taking G as an abstract group;
- termination of the closures of the derived series;
- having a solvable Lie algebra.
To have equivalence one needs to assume G connected. For connected Lie groups, these definitions are the same, and the derived series of Lie algebras are the Lie algebra of the derived series of (closed) subgroups.
See also
- Cartan's criterion
- Killing formKilling formIn mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
- Lie-Kolchin theorem
- SolvmanifoldSolvmanifoldIn mathematics, a solvmanifold is a homogeneous space of a connected solvable Lie group. It may also be characterized as a quotient of a connected solvable Lie group by a closed subgroup...
- Dixmier mapping

