Nilradical of a Lie algebra
Encyclopedia
In algebra
, the nilradical of a Lie algebra
is a nilpotent ideal, which is as large as possible.
The nilradical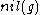
of a finite dimensional Lie algebra 
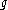is its maximal nilpotent ideal
, which exists because the sum of any two nilpotent ideals is nilpotent. It is an ideal in the radical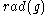
of the Lie algebra 
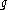. The quotient of a Lie algebra by its nilradical is a reductive Lie algebra 
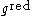. However, the corresponding short exact sequence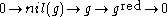
does not split in general (i.e., there isn't always a subalgebra complementary to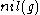
in 
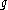). This is in contrast to the Levi decomposition
: the short exact sequence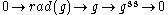
does split (essentially because the quotient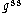
is semisimple).
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the nilradical of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is a nilpotent ideal, which is as large as possible.
The nilradical
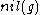of a finite dimensional Lie algebra 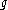is its maximal nilpotent idealNilpotent ideal
In mathematics, more specifically ring theory, an ideal, I, of a ring is said to be a nilpotent ideal, if there exists a natural number k such that Ik = 0. By Ik, it is meant the additive subgroup generated by the set of all products of k elements in I...
, which exists because the sum of any two nilpotent ideals is nilpotent. It is an ideal in the radical
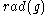of the Lie algebra 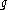. The quotient of a Lie algebra by its nilradical is a reductive Lie algebra 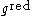. However, the corresponding short exact sequence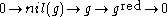does not split in general (i.e., there isn't always a subalgebra complementary to
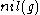in 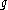). This is in contrast to the Levi decompositionLevi decomposition
In Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra....
: the short exact sequence
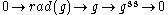
does split (essentially because the quotient
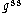is semisimple).