
Klein geometry
Encyclopedia
In mathematics
, a Klein geometry is a type of geometry
motivated by Felix Klein
in his influential Erlangen program
. More specifically, it is a homogeneous space
X together with a transitive action
on X by a Lie group
G, which acts as the symmetry group
of the geometry.
For background and motivation see the article on the Erlangen program
.
and H is a closed
Lie subgroup
of G such that the (left) coset space G/H is connected
. The group G is called the principal group of the geometry and G/H is called the space of the geometry (or, by an abuse of terminology, simply the Klein geometry). The space X = G/H of a Klein geometry is a smooth manifold of dimension
There is a natural smooth left action
of G on X given by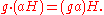
Clearly, this action is transitive (take a = 1), so that one may then regard X as a homogeneous space
for the action of G. The stabilizer of the identity coset H ∈ X is precisely the group H.
Given any connected smooth manifold X and a smooth transitive action by a Lie group G on X, we can construct an associated Klein geometry (G, H) by fixing a basepoint x0 in X and letting H be the stabilizer subgroup of x0 in G. The group H is necessarily a closed subgroup of G and X is naturally diffeomorphic to G/H.
Two Klein geometries (G1, H1) and (G2, H2) are geometrically isomorphic if there is a Lie group isomorphism φ : G1 → G2 so that φ(H1) = H2. In particular, if φ is conjugation
by an element g ∈ G, we see that (G, H) and (G, gHg−1) are isomorphic. The Klein geometry associated to a homogeneous space X is then unique up to isomorphism (i.e. it is independent of the chosen basepoint x0).
of H on G given by right multiplication. This action is both free and proper. The orbits are simply the left coset
s of H in G. One concludes that G has the structure of a smooth principal H-bundle
over the left coset space G/H:

The kernel K may also be described as the core
of H in G (i.e. the largest subgroup of H that is normal
in G). It is the group generated by all the normal subgroups of G that lie in H.
A Klein geometry is said to be effective if K = 1 and locally effective if K is discrete
. If (G, H) is a Klein geometry with kernel K, then (G/K, H/K) is an effective Klein geometry canonically associated to (G, H).
. (This does not imply that G/H is an oriented manifold
). If H is connected it follows that G is also connected (this is because G/H is assumed to be connected, and G → G/H is a fibration
).
Given any Klein geometry (G, H), there is a geometrically oriented geometry canonically associated to (G, H) with the same base space G/H. This is the geometry (G0, G0 ∩ H) where G0 is the identity component
of G. Note that G = G0 H.
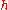 of H has an H-invariant complement in
of H has an H-invariant complement in 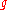 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Klein geometry is a type of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
motivated by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
in his influential Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
. More specifically, it is a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
X together with a transitive action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on X by a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G, which acts as the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the geometry.
For background and motivation see the article on the Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
.
Formal definition
A Klein geometry is a pair (G, H) where G is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and H is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of G such that the (left) coset space G/H is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. The group G is called the principal group of the geometry and G/H is called the space of the geometry (or, by an abuse of terminology, simply the Klein geometry). The space X = G/H of a Klein geometry is a smooth manifold of dimension
- dim X = dim G − dim H.
There is a natural smooth left action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on X given by
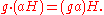
Clearly, this action is transitive (take a = 1), so that one may then regard X as a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
for the action of G. The stabilizer of the identity coset H ∈ X is precisely the group H.
Given any connected smooth manifold X and a smooth transitive action by a Lie group G on X, we can construct an associated Klein geometry (G, H) by fixing a basepoint x0 in X and letting H be the stabilizer subgroup of x0 in G. The group H is necessarily a closed subgroup of G and X is naturally diffeomorphic to G/H.
Two Klein geometries (G1, H1) and (G2, H2) are geometrically isomorphic if there is a Lie group isomorphism φ : G1 → G2 so that φ(H1) = H2. In particular, if φ is conjugation
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
by an element g ∈ G, we see that (G, H) and (G, gHg−1) are isomorphic. The Klein geometry associated to a homogeneous space X is then unique up to isomorphism (i.e. it is independent of the chosen basepoint x0).
Bundle description
Given a Lie group G and closed subgroup H, there is natural right actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of H on G given by right multiplication. This action is both free and proper. The orbits are simply the left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of H in G. One concludes that G has the structure of a smooth principal H-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over the left coset space G/H:

Effective geometries
The action of G on X = G/H need not be effective. The kernel of a Klein geometry is defined to be the kernel of the action of G on X. It is given by
The kernel K may also be described as the core
Core (group)
In group theory, a branch of mathematics, a core is any of certain special normal subgroups of a group. The two most common types are the normal core of a subgroup and the p-core of a group.-Definition:...
of H in G (i.e. the largest subgroup of H that is normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
in G). It is the group generated by all the normal subgroups of G that lie in H.
A Klein geometry is said to be effective if K = 1 and locally effective if K is discrete
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
. If (G, H) is a Klein geometry with kernel K, then (G/K, H/K) is an effective Klein geometry canonically associated to (G, H).
Geometrically oriented geometries
A Klein geometry (G, H) is geometrically oriented if G is connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. (This does not imply that G/H is an oriented manifold
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
). If H is connected it follows that G is also connected (this is because G/H is assumed to be connected, and G → G/H is a fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
).
Given any Klein geometry (G, H), there is a geometrically oriented geometry canonically associated to (G, H) with the same base space G/H. This is the geometry (G0, G0 ∩ H) where G0 is the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of G. Note that G = G0 H.
Reductive geometries
A Klein geometry (G, H) is said to be reductive and G/H a reductive homogeneous space if the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
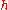 of H has an H-invariant complement in
of H has an H-invariant complement in 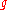 .
.Examples
In the following table, there is a description of the classical geometries, modeled as Klein geometries.| Underlying space | Transformation group G | Subgroup H | Invariants | |
| Euclidean geometry Euclidean geometry Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these... |
Euclidean space Euclidean space In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions... 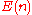 |
Euclidean group Euclidean group In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space... 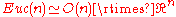 |
Orthogonal group Orthogonal group In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication... 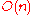 |
Distances of points Euclidean group In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space... , angle Angle In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc... s of vectors |
|---|---|---|---|---|
| Spherical geometry Spherical geometry Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy.... |
Sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... 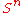 |
Orthogonal group 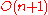 |
Orthogonal group 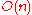 |
Distances of points, angles of vectors |
| Conformal geometry Conformal geometry In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces... on the sphere |
Sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... 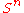 |
Lorentz group Lorentz group In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena... of an  dimensional space dimensional space  |
A subgroup 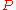 fixing a line fixing a lineLine (geometry) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects... in the null cone of the Minkowski metric |
Angles of vectors |
| Projective geometry Projective geometry In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts... |
Real projective space Real projective space In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...  |
Projective group 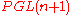 |
A subgroup 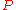 fixing a flag fixing a flag 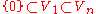 |
Projective line Projective line In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see... s, Cross-ratio Cross-ratio In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line... |
| Affine geometry Affine geometry In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations... |
Affine space Affine space In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point... 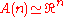 |
Affine group Affine group In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....  |
General linear group General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... GL(n) |
Lines, Quotient of surface areas of geometric shapes, Center of mass Center of mass In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body... of triangless. |
| Hyperbolic geometry Hyperbolic geometry In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced... |
Hyperbolic space Hyperbolic space In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point... 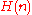 , modeled e.g. as time-like lines in the Minkowski space , modeled e.g. as time-like lines in the Minkowski spaceMinkowski space In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated... 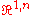 |
Lorentz group 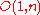 |
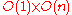 |
Hyperbolic lines, hyperbolic circles, angles. |

