Core (group)
Encyclopedia
In group theory
, a branch of mathematics
, a core is any of certain special normal subgroup
s of a group
. The two most common types are the normal core of a subgroup and the p-core of a group.
of G that is contained in H (or equivalently, the intersection
of the conjugates of H). More generally, the core of H with respect to a subset S⊆G is the intersection of the conjugates of H under S, i.e.
Under this more general definition, the normal core is the core with respect to S=G. The normal core of any normal subgroup is the subgroup itself.
s on sets, where the normal core of the isotropy subgroup of any point acts as the identity on its entire orbit. Thus, in case the action is transitive, the normal core of any isotropy subgroup is precisely the kernel
of the action.
A core-free subgroup is a subgroup whose normal core is the trivial subgroup. Equivalently, it is a subgroup that occurs as the isotropy subgroup of a transitive, faithful group action.
The solution for the hidden subgroup problem
in the abelian
case generalizes to finding the normal core in case of subgroups of arbitrary groups.
, though some aspects generalize to locally finite group
s and to profinite groups.
. It is the normal core of every Sylow p-subgroup of the group. The p-core of G is often denoted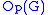
, and in particular appears in one of the definitions of the Fitting subgroup
of a finite group
. Similarly, the p′-core is the largest normal subgroup of G whose order is coprime to p and is denoted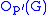
. In the area of finite insoluble groups, including the classification of finite simple groups
, the 2′-core is often called simply the core and denoted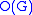
. This causes only a small amount of confusion, because one can usually distinguish between the core of a group and the core of a subgroup within a group. The p′,p-core, denoted 
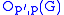is defined by 
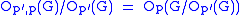. For a finite group, the p′,p-core is the unique largest normal p-nilpotent subgroup.
The p-core can also be defined as the unique largest subnormal p-subgroup; the p′-core as the unique largest subnormal p′-subgroup; and the p′,p-core as the unique largest subnormal p-nilpotent subgroup.
The p′ and p′,p-core begin the upper p-series. For sets π1, π2, ..., πn+1 of primes, one defines subgroups Oπ1, π2, ..., πn+1(G) by: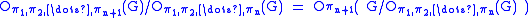
The upper p-series is formed by taking π2i−1 = p′ and π2i = p; there is also a lower p-series. A finite group is said to be p-nilpotent if and only if it is equal to its own p′,p-core. A finite group is said to be p-soluble if and only if it is equal to some term of its upper p-series; its p-length is the length of its upper p-series. A finite group G is said to be p-constrained for a prime p if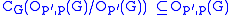
.
Every nilpotent group is p-nilpotent, and every p-nilpotent group is p-soluble. Every soluble group is p-soluble, and every p-soluble group is p-constrained. A group is p-nilpotent if and only if it has a normal p-complement, which is just its p′-core.
s on sets, p-cores and p′-cores are important in modular representation theory
, which studies the actions of groups on vector space
s. The p-core of a finite group is the intersection of the kernels of the irreducible representation
s over any field of characteristic p. For a finite group, the p′-core is the intersection of the kernels of the ordinary (complex) irreducible representations that lie in the principal p-block. For a finite group, the p′,p-core is the intersection of the kernels of the irreducible representations in the principal p-block over any field of characteristic p. Also, for a finite group, the p′,p-core is the intersection of the centralizers of the abelian chief factors whose order is divisible by p (all of which are irreducible representations over a field of size p lying in the principal block). For a finite, p-constrained group, an irreducible module over a field of characteristic p lies in the principal block if and only if the p′-core of the group is contained in the kernel of the representation.
normal subgroup, and is denoted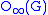
. There is some variance in the literature in defining the p′-core of G. A few authors in only a few papers (for instance Thompson's
N-group papers, but not his later work) define the p′-core of an insoluble group G as the p′-core of its solvable radical in order to better mimic properties of the 2′-core.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a core is any of certain special normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The two most common types are the normal core of a subgroup and the p-core of a group.
Definition
For a group G, the normal core of a subgroup H is the largest normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G that is contained in H (or equivalently, the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the conjugates of H). More generally, the core of H with respect to a subset S⊆G is the intersection of the conjugates of H under S, i.e.
Under this more general definition, the normal core is the core with respect to S=G. The normal core of any normal subgroup is the subgroup itself.
Significance
Normal cores are important in the context of group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s on sets, where the normal core of the isotropy subgroup of any point acts as the identity on its entire orbit. Thus, in case the action is transitive, the normal core of any isotropy subgroup is precisely the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the action.
A core-free subgroup is a subgroup whose normal core is the trivial subgroup. Equivalently, it is a subgroup that occurs as the isotropy subgroup of a transitive, faithful group action.
The solution for the hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
in the abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
case generalizes to finding the normal core in case of subgroups of arbitrary groups.
The p-core
In this section G will denote a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, though some aspects generalize to locally finite group
Locally finite group
In mathematics, in the field of group theory, a locally finite group is a type of group that can be studied in ways analogous to a finite group. Sylow subgroups, Carter subgroups, and abelian subgroups of locally finite groups have been studied....
s and to profinite groups.
Definition
For a prime p, the p-core of a finite group is defined to be its largest normal p-subgroupP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
. It is the normal core of every Sylow p-subgroup of the group. The p-core of G is often denoted
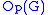, and in particular appears in one of the definitions of the Fitting subgroupFitting subgroup
In mathematics, especially in the area of algebra known as group theory, the Fitting subgroup F of a finite group G, named after Hans Fitting, is the unique largest normal nilpotent subgroup of G. Intuitively, it represents the smallest subgroup which "controls" the structure of G when G is solvable...
of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
. Similarly, the p′-core is the largest normal subgroup of G whose order is coprime to p and is denoted
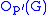. In the area of finite insoluble groups, including the classification of finite simple groupsClassification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, the 2′-core is often called simply the core and denoted
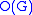. This causes only a small amount of confusion, because one can usually distinguish between the core of a group and the core of a subgroup within a group. The p′,p-core, denoted 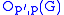is defined by 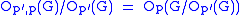. For a finite group, the p′,p-core is the unique largest normal p-nilpotent subgroup.The p-core can also be defined as the unique largest subnormal p-subgroup; the p′-core as the unique largest subnormal p′-subgroup; and the p′,p-core as the unique largest subnormal p-nilpotent subgroup.
The p′ and p′,p-core begin the upper p-series. For sets π1, π2, ..., πn+1 of primes, one defines subgroups Oπ1, π2, ..., πn+1(G) by:
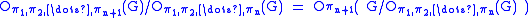
The upper p-series is formed by taking π2i−1 = p′ and π2i = p; there is also a lower p-series. A finite group is said to be p-nilpotent if and only if it is equal to its own p′,p-core. A finite group is said to be p-soluble if and only if it is equal to some term of its upper p-series; its p-length is the length of its upper p-series. A finite group G is said to be p-constrained for a prime p if
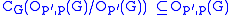.Every nilpotent group is p-nilpotent, and every p-nilpotent group is p-soluble. Every soluble group is p-soluble, and every p-soluble group is p-constrained. A group is p-nilpotent if and only if it has a normal p-complement, which is just its p′-core.
Significance
Just as normal cores are important for group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s on sets, p-cores and p′-cores are important in modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
, which studies the actions of groups on vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. The p-core of a finite group is the intersection of the kernels of the irreducible representation
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
s over any field of characteristic p. For a finite group, the p′-core is the intersection of the kernels of the ordinary (complex) irreducible representations that lie in the principal p-block. For a finite group, the p′,p-core is the intersection of the kernels of the irreducible representations in the principal p-block over any field of characteristic p. Also, for a finite group, the p′,p-core is the intersection of the centralizers of the abelian chief factors whose order is divisible by p (all of which are irreducible representations over a field of size p lying in the principal block). For a finite, p-constrained group, an irreducible module over a field of characteristic p lies in the principal block if and only if the p′-core of the group is contained in the kernel of the representation.
Solvable radicals
A related subgroup in concept and notation is the solvable radical. The solvable radical is defined to be the largest solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
normal subgroup, and is denoted
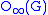. There is some variance in the literature in defining the p′-core of G. A few authors in only a few papers (for instance Thompson'sJohn G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
N-group papers, but not his later work) define the p′-core of an insoluble group G as the p′-core of its solvable radical in order to better mimic properties of the 2′-core.