Hutchinson operator
Encyclopedia
In mathematics
, in the study of fractal
s, a Hutchinson operator (also known as the Barnsley Operator) is a collection of functions on an underlying space E. The iteration
of these functions gives rise to the attractor of an iterated function system
, for which the fixed set is self-similar.
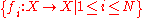be an iterated function system
, or a set of N contractions
from a compact set X to itself. We may regard this as defining an operator H on the power set P X as
where A is any subset of X.
A key question in the theory is to describe the fixed sets of the operator H. One way of constructing such a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the images of Sn under the operator H; then taking S to be the union of the Sn, that is,
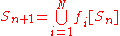
and
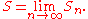
s on a Euclidean space X = Rd. He showed that such a system of functions has a unique compact
(closed and bounded) fixed set S. The proof consists in showing that the Hutchinson operator itself is a contraction mapping on the set of compact subsets of X (endowed with the Hausdorff distance
).
The collection of functions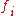
together with composition form a monoid
. With N functions, then one may visualize the monoid as a full N-ary tree
or a Cayley tree.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the study of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s, a Hutchinson operator (also known as the Barnsley Operator) is a collection of functions on an underlying space E. The iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of these functions gives rise to the attractor of an iterated function system
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
, for which the fixed set is self-similar.
Definition
Formally, let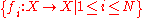 be an iterated function systemIterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
, or a set of N contractions
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
from a compact set X to itself. We may regard this as defining an operator H on the power set P X as
where A is any subset of X.
A key question in the theory is to describe the fixed sets of the operator H. One way of constructing such a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the images of Sn under the operator H; then taking S to be the union of the Sn, that is,
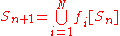
and
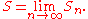
Properties
Hutchinson (1981) considered the case when the fi are contraction mappingContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
s on a Euclidean space X = Rd. He showed that such a system of functions has a unique compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
(closed and bounded) fixed set S. The proof consists in showing that the Hutchinson operator itself is a contraction mapping on the set of compact subsets of X (endowed with the Hausdorff distance
Hausdorff distance
In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
).
The collection of functions
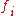together with composition form a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. With N functions, then one may visualize the monoid as a full N-ary tree
K-ary tree
In graph theory, a k-ary tree is a rooted tree in which each node has no more than k children. It is also sometimes known as a k-way tree, an N-ary tree, or an M-ary tree.A binary tree is the special case where k=2....
or a Cayley tree.