Complex base systems
Encyclopedia
In arithmetic
, a complex base system is a positional numeral system whose radix
is an imaginary
(proposed by Donald Knuth
in 1955) or complex number
(proposed by S. Khmelnik in 1964 and Walter F. Penney in 1965).
 (real positive, real with any sign, complex) in this positional number system represented as an expansion
(real positive, real with any sign, complex) in this positional number system represented as an expansion
m - number of discharge, a positive or a negative number (including zero),
 - the radix, the number (real or complex),
- the radix, the number (real or complex),
R - level of decomposition, the number taking values from a finite set
Next, we write the positional number system as follows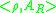 . In particular, the set
. In particular, the set 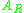 might look like:
might look like:
and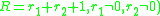 (if
(if 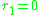 then set
then set 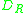 is transformed into set
is transformed into set 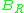 ).
).
Well-known positional number systems of complex numbers include the following. (i represents the imaginary unit.)
s without sign.
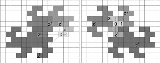
 Base −1±i, using digits 0 and 1, was proposed by S. Khmelnik in 1964 and Walter F. Penney in 1965. The rounding region of an integer – i.e., a set of complex (non-integer) numbers that share the integer part of their representation in this system – has a fractal shape, the twindragon.
Base −1±i, using digits 0 and 1, was proposed by S. Khmelnik in 1964 and Walter F. Penney in 1965. The rounding region of an integer – i.e., a set of complex (non-integer) numbers that share the integer part of their representation in this system – has a fractal shape, the twindragon.
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, a complex base system is a positional numeral system whose radix
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
is an imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
(proposed by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in 1955) or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
(proposed by S. Khmelnik in 1964 and Walter F. Penney in 1965).
In general
In more general cases the number of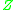 (real positive, real with any sign, complex) in this positional number system represented as an expansion
(real positive, real with any sign, complex) in this positional number system represented as an expansion
-
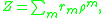 where
where
m - number of discharge, a positive or a negative number (including zero),
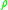 - the radix, the number (real or complex),
- the radix, the number (real or complex), R - level of decomposition, the number taking values from a finite set
-
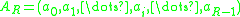 , containing R different numbers
, containing R different numbers 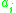 , including complexes,
, including complexes,
Next, we write the positional number system as follows
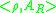 . In particular, the set
. In particular, the set 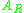 might look like:
might look like:
-
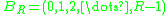 ,
, -
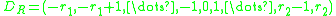 ,
,
and
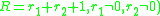 (if
(if 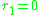 then set
then set 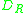 is transformed into set
is transformed into set 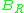 ).
).Well-known positional number systems of complex numbers include the following. (i represents the imaginary unit.)
- Quater-imaginary baseQuater-imaginary baseThe quater-imaginary numeral system was first proposed by Donald Knuth in 1955, in a submission to a high-school science talent search. It is a non-standard positional numeral system which uses the imaginary number 2i as its base. It is able to uniquely represent every complex number using only...
, proposed by Donald KnuthDonald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in 1955: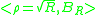 , example,
, example, 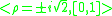 and
and 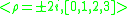 .
.
-
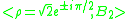 , example,
, example, 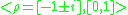 (see also section "Base −1±i" below).
(see also section "Base −1±i" below).
-
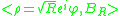 , where
, where 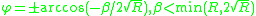 and
and 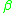 is a positive integer that can take multiple values at a given R.
is a positive integer that can take multiple values at a given R.
-
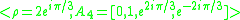 ;
;
-
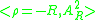 , where the set
, where the set 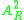 is composed of complex numbers
is composed of complex numbers 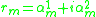 , and numbers
, and numbers 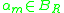 , example, <-2, [0,1,j,1+i]>.
, example, <-2, [0,1,j,1+i]>.
-
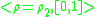 , where
, where 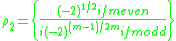 .
.
Binary system
Binary systems of complex numbers, with the digits 0 and 1, are of practical interest. Listed below are those of the system (as a special case shown above systems) and shows code numbers 2, -2, -1. The binary system of real numbers is also listed for comparison.-
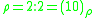 ;
; -
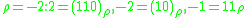 ;
; -
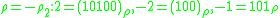 ;
; -
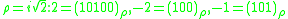 ;
; -
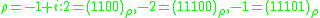 ;
; -
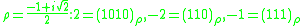 .
.
Base −1±i
Of particular interest, the quater-imaginary system, and base -1±i systems discussed below can be used to finitely represent the Gaussian integerGaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s without sign.

External links
- "Number Systems Using a Complex Base" by Jarek Duda, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
- "The Boundary of Periodic Iterated Function Systems" by Jarek Duda, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
- "Number Systems in 3D" by Jarek Duda, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

