Hyperbolic equilibrium point
Encyclopedia
In the study of dynamical system
s, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point
that does not have any center manifolds
. Near a hyperbolic
point the orbits of a two-dimensional, non-dissipative
system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name – it sounds like it should mean 'saddle point' – but is has become standard." Several properties hold about a neighborhood of a hyperbolic point, notably
is a C1 map and p is a fixed point
then p is said to be a hyperbolic fixed point when the differential
DT(p) has no eigenvalues on the unit circle.
One example of a map
that its only fixed point is hyperbolic is the Arnold Map or cat map:
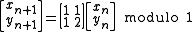
Since the eigenvalues are given by
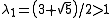
and
.
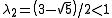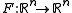
be a C1 (that is, continuously differentiable) vector field
with a critical point p and let J denote the Jacobian matrix of F at p. If the matrix J has no eigenvalues with zero real parts then p is called hyperbolic. Hyperbolic fixed points may also be called hyperbolic critical points or elementary critical points.
The Hartman-Grobman theorem
states that the orbit structure of a dynamical system in a neighbourhood
of a hyperbolic equilibrium point is topologically equivalent to the orbit structure of the linearized
dynamical system.
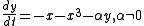
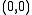is the only equilibrium point. The linearization at the equilibrium is
.
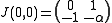The eigenvalues of this matrix are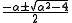
. For all values of 
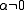, the eigenvalues have non-zero real part. Thus, this equilibrium point is a hyperbolic equilbrium point. The linearized system will behave similar to the non-linear system near 
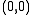. When 
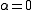, the system has a nonhyperbolic equilibrium at 
.
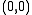Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
that does not have any center manifolds
Center manifold
In mathematics, the center manifold of an equilibrium point of a dynamical system consists of orbits whose behavior around the equilibrium point is not controlled by either the attraction of the stable manifold or the repulsion of the unstable manifold. The first step when studying equilibrium...
. Near a hyperbolic
Hyperbolic
Hyperbolic refers to something related to or in shape of hyperbola , or to something employing the literary device of hyperbole .The following topics are based on the hyperbola etymology:...
point the orbits of a two-dimensional, non-dissipative
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name – it sounds like it should mean 'saddle point' – but is has become standard." Several properties hold about a neighborhood of a hyperbolic point, notably
- A stable manifoldStable manifoldIn mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
and an unstable manifold exist, - ShadowingShadowing lemmaIn the theory of dynamical systems, the shadowing lemma is a lemma describing the behaviour of pseudo-orbits near a hyperbolic invariant set. Informally, it says that every pseudo-orbit stays uniformly close to some true trajectory - in other words, a...
occurs, - The dynamics on the invariant set can be represented via symbolic dynamicsSymbolic dynamicsIn mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
, - A natural measure can be defined,
- The system is structurally stableStructural stabilityIn mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
.
Maps
Ifis a C1 map and p is a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
then p is said to be a hyperbolic fixed point when the differential
Differential
-Mathematics:* Differential comprises multiple related meanings of the word, both in calculus and differential geometry, such as an infinitesimal change in the value of a function* Differential algebra* Differential calculus...
DT(p) has no eigenvalues on the unit circle.
One example of a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
that its only fixed point is hyperbolic is the Arnold Map or cat map:
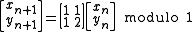
Since the eigenvalues are given by
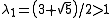
and
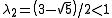.Flows
Let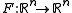be a C1 (that is, continuously differentiable) vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
with a critical point p and let J denote the Jacobian matrix of F at p. If the matrix J has no eigenvalues with zero real parts then p is called hyperbolic. Hyperbolic fixed points may also be called hyperbolic critical points or elementary critical points.
The Hartman-Grobman theorem
Hartman-Grobman theorem
In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point....
states that the orbit structure of a dynamical system in a neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of a hyperbolic equilibrium point is topologically equivalent to the orbit structure of the linearized
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
dynamical system.
Example
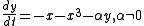
Consider the nonlinear system 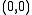is the only equilibrium point. The linearization at the equilibrium is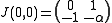.The eigenvalues of this matrix are
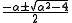. For all values of 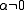, the eigenvalues have non-zero real part. Thus, this equilibrium point is a hyperbolic equilbrium point. The linearized system will behave similar to the non-linear system near 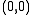. When 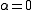, the system has a nonhyperbolic equilibrium at .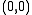