Hartman-Grobman theorem
Encyclopedia
In mathematics
, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood
of a hyperbolic equilibrium point
.
Basically the theorem states that the behaviour of a dynamical system near a hyperbolic equilibrium point is qualitatively the same as the behaviour of its linearization
near this equilibrium point provided that no eigenvalue of the linearization has its real part equal to 0. Therefore when dealing with such fixed points one can use the simpler linearization of the system to analyze its behaviour.
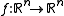
be a smooth map with a hyperbolic equilibrium point p, that is : f(p)=0 and no eigenvalue of the linearization A of f at point p has its real part equal to 0. Then there exists a neighborhood U of p and a homeomorphism
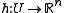
such that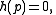
and such that in a neighbourhood U of p, the flow
of f is topologically conjugate by h to the flow of its linearization A.
In general, even for infinitely differentiable maps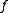
, the homeomorphism 
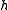need not to be smooth, nor even locally Lipschitz. However, it turns out to be Hölder continuous, with an exponent depending on the constant of hyperbolicity of A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of a hyperbolic equilibrium point
Hyperbolic equilibrium point
In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general...
.
Basically the theorem states that the behaviour of a dynamical system near a hyperbolic equilibrium point is qualitatively the same as the behaviour of its linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
near this equilibrium point provided that no eigenvalue of the linearization has its real part equal to 0. Therefore when dealing with such fixed points one can use the simpler linearization of the system to analyze its behaviour.
Main theorem
Let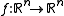be a smooth map with a hyperbolic equilibrium point p, that is : f(p)=0 and no eigenvalue of the linearization A of f at point p has its real part equal to 0. Then there exists a neighborhood U of p and a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
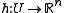
such that
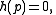
and such that in a neighbourhood U of p, the flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
of f is topologically conjugate by h to the flow of its linearization A.
In general, even for infinitely differentiable maps
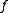, the homeomorphism 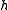need not to be smooth, nor even locally Lipschitz. However, it turns out to be Hölder continuous, with an exponent depending on the constant of hyperbolicity of A.