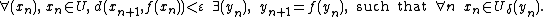Shadowing lemma
Encyclopedia
In the theory of dynamical systems
, the shadowing lemma is a lemma
describing the behaviour of pseudo-orbits near a hyperbolic invariant set
. Informally, it says that every pseudo-orbit (which one can think as of a numerically computed trajectory with rounding errors on every step) stays uniformly close to some true trajectory (with slightly altered initial position) - in other words, a pseudo-trajectory is "shadowed" by a true one.
(X, d) to itself, define a ε-pseudo-orbit (or ε-orbit) as a sequence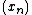
of points such that 
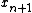belongs to a ε-neighborhood of 
.
Then, near a hyperbolic invariant set, the following statement holds:
Let Λ be a hyperbolic invariant set of a diffeomorphism
f. There exists a neighborhood U of Λ with the following property: for any δ > 0 there exists ε > 0, such that any (finite or infinite) ε-pseudo-orbit that stays in U also stays in a δ-neighborhood of some true orbit.
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
, the shadowing lemma is a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
describing the behaviour of pseudo-orbits near a hyperbolic invariant set
Hyperbolic set
In dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
. Informally, it says that every pseudo-orbit (which one can think as of a numerically computed trajectory with rounding errors on every step) stays uniformly close to some true trajectory (with slightly altered initial position) - in other words, a pseudo-trajectory is "shadowed" by a true one.
Formal statement
Given a map f : X → X of a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(X, d) to itself, define a ε-pseudo-orbit (or ε-orbit) as a sequence
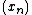of points such that 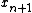belongs to a ε-neighborhood of .Then, near a hyperbolic invariant set, the following statement holds:
Let Λ be a hyperbolic invariant set of a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
f. There exists a neighborhood U of Λ with the following property: for any δ > 0 there exists ε > 0, such that any (finite or infinite) ε-pseudo-orbit that stays in U also stays in a δ-neighborhood of some true orbit.