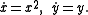In mathematics, the center manifold of an equilibrium point of a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

 consists of orbits whose behavior around the equilibrium point is not controlled by either the attraction of the stable manifold

Stable manifold

In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...

 or the repulsion of the unstable manifold. The first step when studying equilibrium points of dynamical systems is to linearize the system. The eigenvectors corresponding to eigenvalues with negative real part form the stable eigenspace, which gives rise to the stable manifold. The stable manifold attracts orbits close to it. Similarly, eigenvalues with positive real part yield the unstable manifold, which repels orbits close to it.

This concludes the story if the equilibrium point is hyperbolic

Hyperbolic equilibrium point

In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general...

 (i.e., all eigenvalues of the linearization have nonzero real part). However, if there are eigenvalues whose real part is zero, then these give rise to the center manifold. The behavior near the center manifold is not determined by the linearization and thus more difficult to study.

Center manifolds play an important role in bifurcation theory

Bifurcation theory

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...

 because the interesting behavior takes place on the center manifold.

Definition

Let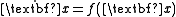


be a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

 with equilibrium point x*.

The linearization of the system at the equilibrium point is


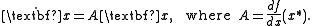
The matrix A defines three subspaces:

• the stable subspace, which is spanned by the generalized eigenvector
  Generalized eigenvector
  In linear algebra, for a matrix A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity...
  
  s corresponding to the eigenvalues λ with Re λ < 0;
• the unstable subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues λ with Re λ > 0;
• the center subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues λ with Re λ = 0.

These spaces are all invariant subspace

Invariant subspace

In mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...

s of the linearized equation.

Corresponding to the linearized system, the nonlinear system has invariant manifold

Invariant manifold

In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system. An example is the stable manifold....

s, consisting of orbits of the nonlinear system. There is an invariant manifold tangent to the stable subspace and with the same dimension; this manifold is the stable manifold

Stable manifold

In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...

. Similarly, the unstable manifold is tangent to the unstable subspace, and the center manifold is tangent to the center subspace. If, as is common, the eigenvalues of the center subspace are all precisely zero, rather than just real part zero, then a center manifold is often called a slow manifold

Slow manifold

In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory...

.

The center manifold theorem

The center manifold theorem states that if ƒ is C^r (r times continuously differentiable), then at every equilibrium point there is a unique C^r stable manifold, a unique C^r unstable manifold, and a (not necessarily unique) C^r−1 center manifold.

In example applications, a nonlinear coordinate transform to a normal form (mathematics) can clearly separate these three manifolds. A web service http://www.maths.adelaide.edu.au/anthony.roberts/sdenf.php currently undertakes the necessary computer algebra for a range of finite dimensional systems.

There is theory for the existence and relevance of center manifolds in infinite dimensional dynamical systems . The general theory currently only applies when the center manifold itself is of finite dimension. However, some applications, such as to shear dispersion, can justify and construct an infinite dimensional center manifold.

Center manifold and the analysis of nonlinear systems

As the stability of the equilibrium correlates with the "stability" of its manifolds, the existence of a center manifold brings up the question about the dynamics on the center manifold. This is analyzed by the center manifold reduction, which, in combination with some system-parameter μ, leads to the concepts of bifurcations

Bifurcation theory

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...

.

Correspondingly, a web service http://www.maths.adelaide.edu.au/anthony.roberts/sdesm.php currently undertakes the necessary computer algebra to construct just the center manifold for a range of finite dimensional systems.

A simple example

Consider the system

The unstable manifold at the origin is the y axis, and the stable manifold is the trivial set {(0, 0)}. Any orbit not on the stable manifold satisfies an equation on the form 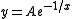for some real constant A. It follows that for any real A, we can create a center manifold by piecing together the curve 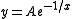for x > 0 with the negative x axis (including the origin). Moreover, all center manifolds have this potential non-uniqueness, although often the non-uniqueness only occurs in unphysical complex values of the variables.

The wikipedia entry on slow manifold

Slow manifold

In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory...

s gives more examples.