
Heegner number
Encyclopedia
In number theory
, a Heegner number is a square-free positive integer
d such that the imaginary quadratic field Q(√−d) has class number
1. Equivalently, its ring of integers
has unique factorization.
The determination of such numbers is a special case of the class number problem, and they underlie several striking results in number theory.
According to the Stark–Heegner theorem
there are precisely nine Heegner numbers:
This result was conjectured by Gauss
and proven by Kurt Heegner
in 1952.
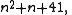
which gives (distinct) primes for n = 0, ..., 39, is related to the Heegner number 163 = 4 · 41 − 1.
Rabinowitz proved that
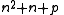
gives primes for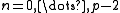 if and only if its discriminant
if and only if its discriminant 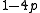 equals minus a Heegner number.
equals minus a Heegner number.
(Note that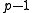 yields
yields  , so
, so  is maximal.)
is maximal.)
1, 2, and 3 are not of the required form, so the Heegner numbers that work are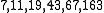 , yielding prime generating functions of Euler's form for
, yielding prime generating functions of Euler's form for  ; these latter numbers are called lucky numbers of Euler
; these latter numbers are called lucky numbers of Euler
by F. Le Lionnais
.
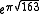 , which is an almost integer, in that it is very close to an integer
, which is an almost integer, in that it is very close to an integer
:
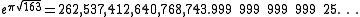
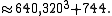
This number was discovered in 1859 by the mathematician Charles Hermite
.
In a 1975 April Fool
article in Scientific American
magazine, "Mathematical Games" columnist Martin Gardner
made the (hoax) claim that the number was in fact an integer, and that the Indian mathematical genius Srinivasa Ramanujan
had predicted it—hence its name.
This coincidence is explained by complex multiplication
and the q-expansion of the j-invariant
.
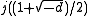 is an integer for d a Heegner number, and
is an integer for d a Heegner number, and  via the q-expansion.
via the q-expansion.
If is a quadratic irrational, then the j-invariant is an algebraic integer
is a quadratic irrational, then the j-invariant is an algebraic integer
of degree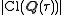 , the class number of
, the class number of 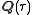 and the minimal (monic integral) polynomial it satisfies is called the Hilbert class polynomial. Thus if the imaginary quadratic extension
and the minimal (monic integral) polynomial it satisfies is called the Hilbert class polynomial. Thus if the imaginary quadratic extension 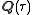 has class number 1 (so d is a Heegner number), the j-invariant is an integer.
has class number 1 (so d is a Heegner number), the j-invariant is an integer.
The q-expansion of j, with its Fourier series
expansion written as a Laurent series
in terms of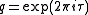 , begins as:
, begins as:

The coefficients asymptotically grow as
asymptotically grow as 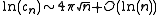 , and the low order coefficients grow more slowly than
, and the low order coefficients grow more slowly than 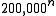 , so for
, so for  , j is very well approximated by its first two terms. Setting
, j is very well approximated by its first two terms. Setting 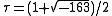 yields
yields 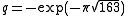 or equivalently,
or equivalently, 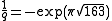 . Now
. Now 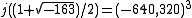 , so,
, so,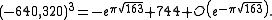
Or,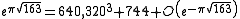
where the linear term of the error is,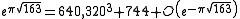
explaining why is within approximately the above of being an integer.
is within approximately the above of being an integer.
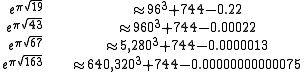
Alternatively,
where the reason for the squares is due to certain Eisenstein series
. For Heegner numbers d < 19, one does not obtain an almost integer; even d = 19 is not noteworthy. The integer j-invariants are highly factorable, which follows from the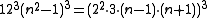 form, and factor as,
form, and factor as,
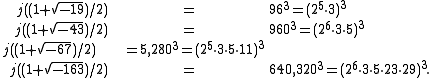
These transcendental numbers, in addition to being closely approximated by integers, (which are simply algebraic numbers of degree 1), can also be closely approximated by algebraic numbers of degree 3,

The roots of the cubics can be exactly given by quotients of the Dedekind eta function
η(τ), a modular function involving a 24th root, and which explains the 24 in the approximation. In addition, they can also be closely approximated by algebraic numbers of degree 4,

Note the reappearance of the integers n = {3, 9 , 21, 231} as well as the fact that,
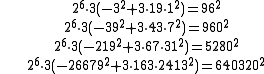
which, with the appropriate fractional power, are precisely the j-invariants. As well as for algebraic numbers of degree 6,
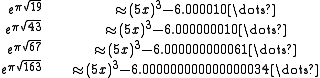
where the x's are given respectively by the appropriate root of the sextic equation
s,

with the j-invariants appearing again. These sextics are not only algebraic, they are also solvable
in radicals
as they factor into two cubics over the extension (with the first factoring further into two quadratics
(with the first factoring further into two quadratics
). These algebraic approximations can be exactly expressed in terms of Dedekind eta quotients. As an example, let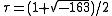 , then,
, then,
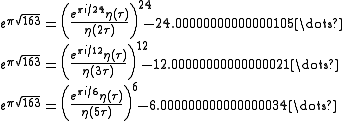
where the eta quotients are the algebraic numbers given above.
d = −4×58 with class number h(d) = 2, one obtains: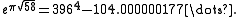
This result was used by Ramanujan
to give a fast converging series expansion for π.
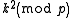 for
for 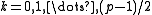 (this is sufficient because
(this is sufficient because 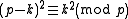 ), one gets consecutive composites, followed by consecutive primes, if and only if p is a Heegner number.
), one gets consecutive composites, followed by consecutive primes, if and only if p is a Heegner number.
For details, see "Quadratic Polynomials Producing Consecutive Distinct Primes and Class Groups of Complex Quadratic Fields" by Richard Mollin.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Heegner number is a square-free positive integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
d such that the imaginary quadratic field Q(√−d) has class number
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
1. Equivalently, its ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
has unique factorization.
The determination of such numbers is a special case of the class number problem, and they underlie several striking results in number theory.
According to the Stark–Heegner theorem
Stark–Heegner theorem
In number theory, a branch of mathematics, the Stark–Heegner theorem states precisely which quadratic imaginary number fields admit unique factorisation in their ring of integers...
there are precisely nine Heegner numbers:
- , , , , , , , , .
This result was conjectured by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and proven by Kurt Heegner
Kurt Heegner
Kurt Heegner was a German private scholar from Berlin, who specialized inradio engineering and mathematics...
in 1952.
Euler's prime-generating polynomial
Euler's prime-generating polynomial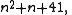
which gives (distinct) primes for n = 0, ..., 39, is related to the Heegner number 163 = 4 · 41 − 1.
Rabinowitz proved that
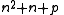
gives primes for
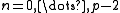 if and only if its discriminant
if and only if its discriminant 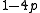 equals minus a Heegner number.
equals minus a Heegner number.(Note that
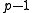 yields
yields  , so
, so  is maximal.)
is maximal.)1, 2, and 3 are not of the required form, so the Heegner numbers that work are
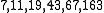 , yielding prime generating functions of Euler's form for
, yielding prime generating functions of Euler's form for  ; these latter numbers are called lucky numbers of Euler
; these latter numbers are called lucky numbers of EulerLucky numbers of Euler
Euler's "lucky" numbers are positive integers n such that m2 − m + n is a prime number for m = 0, …, n − 1.Leonhard Euler published the polynomial x2 − x + 41 which produces prime numbers for all integer values of x from 0 to 40. Obviously, when x is equal to 41, the value cannot be prime...
by F. Le Lionnais
François Le Lionnais
François Le Lionnais was a French chemical engineer and mathematician, perhaps best known as a founder of the literary movement Oulipo....
.
Almost integers and Ramanujan's constant
Ramanujan's constant is the transcendental numberTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
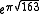 , which is an almost integer, in that it is very close to an integer
, which is an almost integer, in that it is very close to an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
:
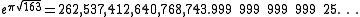
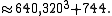
This number was discovered in 1859 by the mathematician Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
.
In a 1975 April Fool
April Fools' Day
April Fools' Day is celebrated in different countries around the world on April 1 every year. Sometimes referred to as All Fools' Day, April 1 is not a national holiday, but is widely recognized and celebrated as a day when many people play all kinds of jokes and foolishness...
article in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
magazine, "Mathematical Games" columnist Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
made the (hoax) claim that the number was in fact an integer, and that the Indian mathematical genius Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
had predicted it—hence its name.
This coincidence is explained by complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
and the q-expansion of the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
.
Detail
Briefly,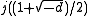 is an integer for d a Heegner number, and
is an integer for d a Heegner number, and  via the q-expansion.
via the q-expansion.If
 is a quadratic irrational, then the j-invariant is an algebraic integer
is a quadratic irrational, then the j-invariant is an algebraic integerAlgebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
of degree
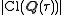 , the class number of
, the class number of 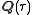 and the minimal (monic integral) polynomial it satisfies is called the Hilbert class polynomial. Thus if the imaginary quadratic extension
and the minimal (monic integral) polynomial it satisfies is called the Hilbert class polynomial. Thus if the imaginary quadratic extension 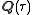 has class number 1 (so d is a Heegner number), the j-invariant is an integer.
has class number 1 (so d is a Heegner number), the j-invariant is an integer.The q-expansion of j, with its Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
expansion written as a Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in terms of
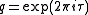 , begins as:
, begins as:
The coefficients
 asymptotically grow as
asymptotically grow as 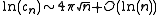 , and the low order coefficients grow more slowly than
, and the low order coefficients grow more slowly than 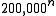 , so for
, so for  , j is very well approximated by its first two terms. Setting
, j is very well approximated by its first two terms. Setting 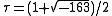 yields
yields 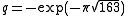 or equivalently,
or equivalently, 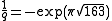 . Now
. Now 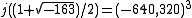 , so,
, so,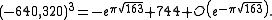
Or,
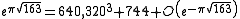
where the linear term of the error is,
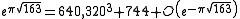
explaining why
 is within approximately the above of being an integer.
is within approximately the above of being an integer.Other Heegner numbers
For the four largest Heegner numbers, the approximations one obtains are as follows.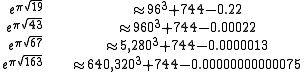
Alternatively,

where the reason for the squares is due to certain Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
. For Heegner numbers d < 19, one does not obtain an almost integer; even d = 19 is not noteworthy. The integer j-invariants are highly factorable, which follows from the
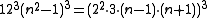 form, and factor as,
form, and factor as,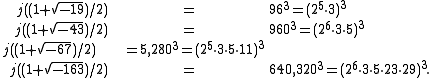
These transcendental numbers, in addition to being closely approximated by integers, (which are simply algebraic numbers of degree 1), can also be closely approximated by algebraic numbers of degree 3,

The roots of the cubics can be exactly given by quotients of the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
η(τ), a modular function involving a 24th root, and which explains the 24 in the approximation. In addition, they can also be closely approximated by algebraic numbers of degree 4,

Note the reappearance of the integers n = {3, 9 , 21, 231} as well as the fact that,
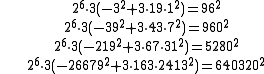
which, with the appropriate fractional power, are precisely the j-invariants. As well as for algebraic numbers of degree 6,
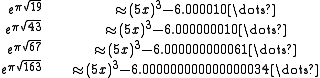
where the x's are given respectively by the appropriate root of the sextic equation
Sextic equation
In mathematics, a sextic equation is a polynomial equation of degree six. It is of the form:ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\,where a \neq 0....
s,

with the j-invariants appearing again. These sextics are not only algebraic, they are also solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
in radicals
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
as they factor into two cubics over the extension
 (with the first factoring further into two quadratics
(with the first factoring further into two quadraticsQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
). These algebraic approximations can be exactly expressed in terms of Dedekind eta quotients. As an example, let
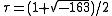 , then,
, then,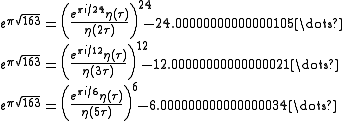
where the eta quotients are the algebraic numbers given above.
Higher class numbers
One gets other almost integers for other class numbers. Taking the fundamental discriminantFundamental discriminant
In mathematics, a fundamental discriminant D is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of Q. Conversely, every integer D with is the discriminant of some binary quadratic form with integer...
d = −4×58 with class number h(d) = 2, one obtains:
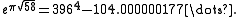
This result was used by Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
to give a fast converging series expansion for π.
Consecutive primes
Given an odd prime p, if one computes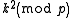 for
for 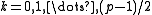 (this is sufficient because
(this is sufficient because 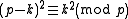 ), one gets consecutive composites, followed by consecutive primes, if and only if p is a Heegner number.
), one gets consecutive composites, followed by consecutive primes, if and only if p is a Heegner number.For details, see "Quadratic Polynomials Producing Consecutive Distinct Primes and Class Groups of Complex Quadratic Fields" by Richard Mollin.
External links
- Gauss' Class Number Problem for Imaginary Quadratic Fields, by Dorian Goldfeld: Detailed history of problem.

