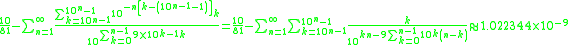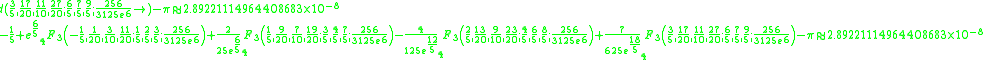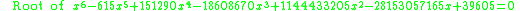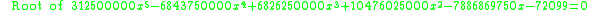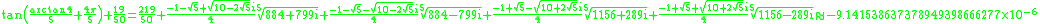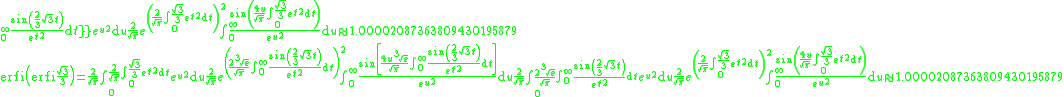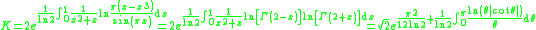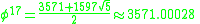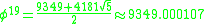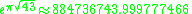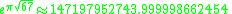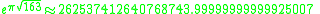Almost integer
Encyclopedia
In recreational mathematics
an almost integer is any number that is very close to an integer
. Well known examples of almost integers are high powers of the golden ratio
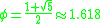 , for example:
, for example:
The fact that these powers approach integers is non-coincidental, which is trivially seen because the golden ratio is a Pisot-Vijayaraghavan number
.
Other occurrences of non-coincidental near-integers involve the three largest Heegner number
s:
where the non-coincidence can be better appreciated when expressed in the common simple form: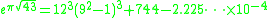
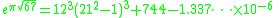
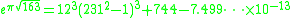
where :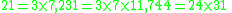
and the reason for the squares being due to certain Eisenstein series
. The constant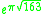
is sometimes referred to as Ramanujan's constant.
Almost integers involving the mathematical constants pi
and e
have often puzzled mathematicians. An example is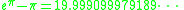
To date, no explanation has been given for why Gelfond's constant
(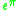 ) is nearly identical to
) is nearly identical to 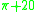 , which is therefore regarded to be a mathematical coincidence.
, which is therefore regarded to be a mathematical coincidence.
Another example is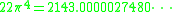
Also consider π in cubic expressions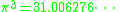
or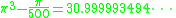
where the second one is obvious from the first one.
Also consider π in quadratic expressions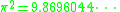
or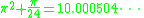
where the second one is obvious from the first one.
Here are more examples:
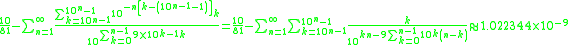
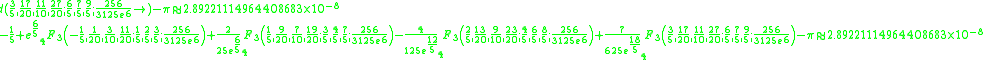
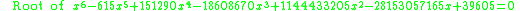

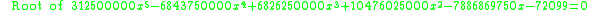
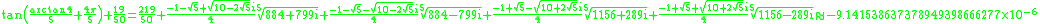
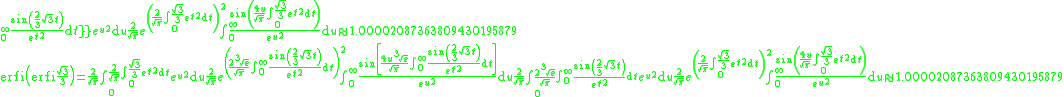
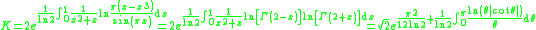
Recreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
an almost integer is any number that is very close to an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. Well known examples of almost integers are high powers of the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
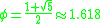 , for example:
, for example:
The fact that these powers approach integers is non-coincidental, which is trivially seen because the golden ratio is a Pisot-Vijayaraghavan number
Pisot-Vijayaraghavan number
In mathematics, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real algebraic integer greater than 1 such that all its Galois conjugates are less than 1 in absolute value. These numbers were discovered by Axel Thue in 1912 and rediscovered by G. H. Hardy in...
.
Other occurrences of non-coincidental near-integers involve the three largest Heegner number
Heegner number
In number theory, a Heegner number is a square-free positive integer d such that the imaginary quadratic field Q has class number 1...
s:
where the non-coincidence can be better appreciated when expressed in the common simple form:
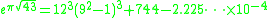
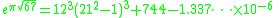
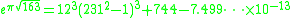
where :
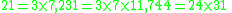
and the reason for the squares being due to certain Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
. The constant
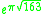
is sometimes referred to as Ramanujan's constant.
Almost integers involving the mathematical constants pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
and e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
have often puzzled mathematicians. An example is
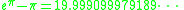
To date, no explanation has been given for why Gelfond's constant
Gelfond's constant
In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
(
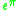 ) is nearly identical to
) is nearly identical to 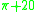 , which is therefore regarded to be a mathematical coincidence.
, which is therefore regarded to be a mathematical coincidence.Another example is
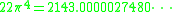
Also consider π in cubic expressions
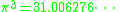
or
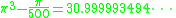
where the second one is obvious from the first one.
Also consider π in quadratic expressions
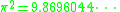
or
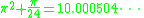
where the second one is obvious from the first one.
Here are more examples:
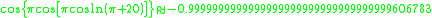 |
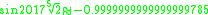 |
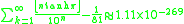 |
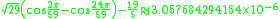 |
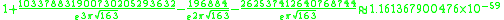 |
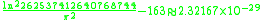 |
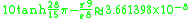 |
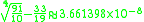 |
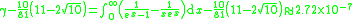 |
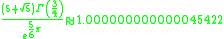 |
 |
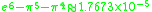 |
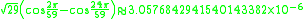 |
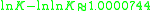 |
 |
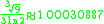 |
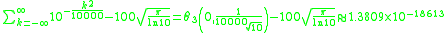 |
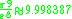 |
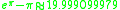 |
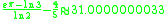 |
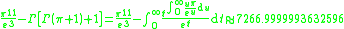 |
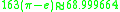 |
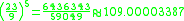 |
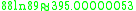 |
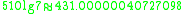 |
 |
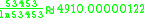 |
 |
 |
 |
 |
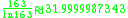 |
 |