
Petersson inner product
Encyclopedia
In mathematics
the Petersson inner product is an inner product defined on the space
of entire modular form
s. It was introduced by the German mathematician Hans Petersson
.
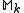 be the space of entire modular forms of weight
be the space of entire modular forms of weight 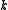 and
and
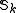 the space of cusp form
the space of cusp form
s.
The mapping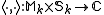 ,
,

is called Petersson inner product, where
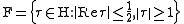
is a fundamental region of the modular group
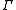 and for
and for 
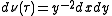
is the hyperbolic volume form.
For the Hecke operator
s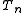 we have:
we have:
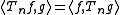
This can be used to show that the space of cusp forms has an orthonormal basis consisting of
simultaneous eigenfunction
s for the Hecke operators and the Fourier coefficients of these
forms are all real.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Petersson inner product is an inner product defined on the space
of entire modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. It was introduced by the German mathematician Hans Petersson
Hans Petersson
Hans Petersson was a German mathematician. He introduced the Petersson inner product and is also known for the Ramanujan–Petersson conjecture.-References:...
.
Definition
Let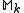 be the space of entire modular forms of weight
be the space of entire modular forms of weight 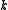 and
and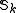 the space of cusp form
the space of cusp formCusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
s.
The mapping
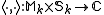 ,
,
is called Petersson inner product, where
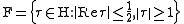
is a fundamental region of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
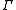 and for
and for 
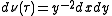
is the hyperbolic volume form.
Properties
The integral is absolutely convergent and the Petersson inner product is a positive definite Hermite form.For the Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s
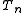 we have:
we have: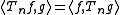
This can be used to show that the space of cusp forms has an orthonormal basis consisting of
simultaneous eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s for the Hecke operators and the Fourier coefficients of these
forms are all real.

