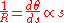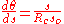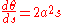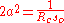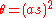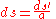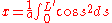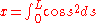An Euler spiral is a curve whose curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals.

Euler spirals have applications to diffraction

Diffraction

Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...

 computations. They are also widely used as transition curve in railroad engineering

Railway systems engineering

Railway systems engineering is a multi-faceted engineering discipline dealing with the design, construction and operation of all types of railway systems....

/highway engineering

Highway engineering

Highway engineering is an engineering discipline branching from civil engineering which involves the design, construction and maintenance of Highway Systems. Highway Engineering become prominent towards the latter half of the 20th Century after World War 2. Standards of highway engineering are...

 for connecting and transiting the geometry between a tangent and a circular curve. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral:

• Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length.
• Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter.

Track transition curve

An object traveling on a circular path experiences a centripetal acceleration

Uniform circular motion

In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...

. When a vehicle traveling on a straight path approaches a circular path, it experiences a sudden centripetal acceleration starting at the tangent point; and thus centripetal force acts instantly causing much discomfort.

On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary so that the centripetal acceleration increases linearly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance. This geometry is an Euler spiral.

Unaware of the solution of the geometry by Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

, Rankine

William John Macquorn Rankine

William John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....

 cited the cubic curve (a polynomial curve of degree 3), which is an approximation of the Euler spiral for small angular changes in the same way that a parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

 is an approximation to a circular curve.

Marie Alfred Cornu

Marie Alfred Cornu

Marie Alfred Cornu was a French physicist. The French generally refer to him as Alfred Cornu.Cornu was born at Orléans and was educated at the École polytechnique and the École des mines...

 (and later some civil engineers) also solved the calculus of Euler spiral independently. Euler spirals are now widely used in rail and highway engineering for providing a transition or an easement between a tangent and a horizontal circular curve.

Symbols

	Radius of curvature
	Radius of Circular curve at the end of the spiral
	Angle of curve from beginning of spiral (infinite ) to a particular point on the spiral.
	This can also be measured as the angle between the initial tangent and the tangent at the concerned point.
	Angle of full spiral curve
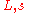	Length measured along the spiral curve from its initial position
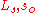	Length of spiral curve

Derivation

The graph on the right illustrates an Euler spiral used as an easement (transition) curve between two given curves, in this case a straight line (the negative x axis) and a circle. The spiral starts at the origin in the positive x direction and gradually turns anticlockwise to osculate the circle.

The spiral is a small segment of the above double-end Euler spiral in the first quadrant.

From the definition of the curvature,

i.e.

We write in the format,

Where

Or

Thus

Now

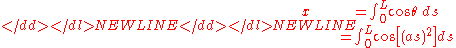
If

Then

Thus

Expansion of Fresnel integral

If a = 1, which is the case for normalized Euler curve, then the Cartesian coordinates are given by Fresnel integrals (or Euler integrals):


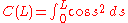
Expand C(L) according to power series expansion of cosine:



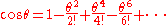
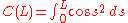
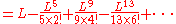
Expand S(L) according to power series expansion of sine:

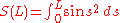
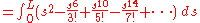
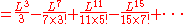
Normalization and conclusion

For a given Euler curve with:


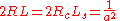
or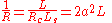

then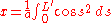


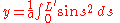
where and .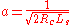

The process of obtaining solution of of an Euler spiral can thus be described as:

• Map L of the original Euler spiral by multiplying with factor to 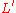of the normalized Euler spiral;
• Find from the Fresnel integrals; and
• Map to by scaling up (denormalize) with factor 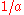. Note that .

In the normalization process,


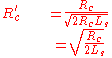
Then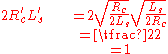

Generally the normalization reduces L' to a small value (<1) and results in good converging characteristics of the Fresnel integral manageable with only a few terms (at a price of increased numerical instability

Numerical stability

In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....

 of the calculation, esp. for bigger values.).

Illustration

Given: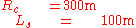
Then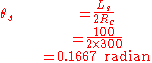
And

We scale down the Euler spiral by √60,000, i.e.100√6 to normalized Euler spiral that has:

And

The two angles are the same. This thus confirm that the original and normalized Euler spirals are having geometric similarity. The locus of the normalized curve can be determined from Fresnel Integral, while the locus of the original Euler spiral can be obtained by scaling back / up or denormalizing.

Other properties of normalized Euler spiral

Normalized Euler spiral can be expressed as:

Normalized Euler spiral has the following properties:



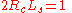
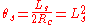
And


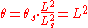
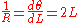
Note that also means 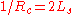, in agreement with the last mathematical statement.

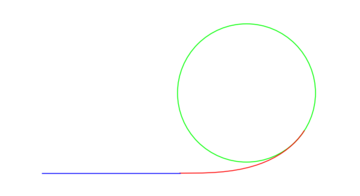
Code for producing an Euler spiral

The following Sage code produces the second graph above. The first four lines express the Euler spiral component. Fresnel functions could not be found. Instead, the integrals of two expanded Taylor series are adopted. The remaining code expresses respectively the tangent and the circle, including the computation for the center coordinates.

var('L')
p = integral(taylor(cos(L^2), L, 0, 12), L)
q = integral(taylor(sin(L^2), L, 0, 12), L)
r1 = parametric_plot([p, q], (L, 0, 1), color = 'red')

r2 = line([(-1.0, 0), (0,0)], rgbcolor = 'blue')

x1 = p.subs(L = 1)
y1 = q.subs(L = 1)
R = 0.5
x2 = x1 - R*sin(1.0)
y2 = y1 + R*cos(1.0)
r3 = circle((x2, y2), R, rgbcolor = 'green')
show(r1 + r2 + r3, aspect_ratio = 1, axes=false)

The following is Mathematica

Mathematica

Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...

code for the Euler spiral component (it works directly in wolframalpha.com):

ParametricPlot[
{FresnelC[Sqrt[2/\[Pi]] t]/Sqrt[2/\[Pi]],
FresnelS[Sqrt[2/\[Pi]] t]/Sqrt[2/\[Pi]]},
{t, -10, 10}]

External links

• Euler's spiral at 2-D Mathematical Curves
• Interactive example with JSXGraph

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.