
Track transition curve
Encyclopedia

Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
. In plan (i.e., the horizontal curve) the start of the transition is at infinite radius and at the end of the transition it has the same radius as the curve itself, thus forming a very broad spiral. At the same time, in the vertical plane, the outside of the curve is gradually raised until the correct degree of bank
Cant (road/rail)
The cant of a railway track or a road is the difference in elevation between the two edges...
is reached.
If such easement were not applied, the lateral acceleration of a rail vehicle would change abruptly at one point – the tangent point
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
where the straight track meets the curve – with undesirable results. With a road vehicle the driver naturally applies the steering alteration in a gradual manner and the curve is designed to permit this, using the same principle.
History
On early railroadsHistory of rail transport
The history of rail transport dates back nearly 500 years and includes systems with man or horse power and rails of wood or stone. Modern rail transport systems first appeared in England in the 1820s...
, because of the low speeds and wide-radius curves employed, the surveyors were able to ignore any form of easement, but during the 19th century, as speeds increased, the need for a track curve with gradually increasing curvature became apparent. Rankine's
William John Macquorn Rankine
William John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....
1862 "Civil Engineering" cites several such curves, including an 1828 or 1829 proposal based on the "curve of sines
Sine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
" by William Gravatt, and the curve of adjustment by William Froude
William Froude
William Froude was an English engineer, hydrodynamicist and naval architect. He was the first to formulate reliable laws for the resistance that water offers to ships and for predicting their stability....
around 1842 approximating the elastic curve
Elastica theory
The elastica theory is a theory of mechanics of solid materials developed by Leonhard Euler that allows for very large scale elastic deflections of structures. Euler and Jakob Bernoulli developed the theory for elastic lines and studied buckling. Certain situations can be solved exactly by...
. The actual equation given in Rankine is that of a cubic curve, which is a polynomial curve of degree 3. This was also known as cubic parabola at that time.
In the UK, only from 1845 when legislation and land costs began to constrain the laying out of rail routes and tighter curves were necessary, did the principles start to be applied in practice.
The "true spiral", where the curvature is exactly linear in arclength, requires more sophisticated mathematics (in particular, the ability to integrate its intrinsic equation) to compute than the proposals cited by Rankine. Several late-19th century civil engineers seem to have derived the equation for this curve independently (all unaware of the original characterization of this curve by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1744). Charles Crandall gives credit to one Ellis Holbrook, in the Railroad Gazette, Dec. 3, 1880, for the first accurate description of the curve. Another early publication was The Railway Transition Spiral by Arthur N. Talbot, originally published in 1890. Some early 20th century authors call the curve "Glover's spiral", attributing it to James Glover's 1900 publication.
The equivalence of the railroad transition spiral and the clothoid seems to have been first published in 1922 by Arthur Lovat Higgins. Since then, "clothoid" is the most common name given the curve, even though the correct name (following standards of academic attribution) is "the Euler spiral".
Geometry
While railroad track geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
is intrinsically three-dimensional
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
, for practical purposes the vertical and horizontal components of track geometry are usually treated separately.
The overall design pattern for the vertical geometry is typically a sequence of constant grade segments connected by vertical transition curves in which the local grade varies linearly with distance and in which the elevation therefore varies quadratically
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
with distance. Here grade refers to the tangent of the angle of rise of the track. The design pattern for horizontal geometry is typically a sequence of straight line (i.e., a tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
) and curve (i.e. a circular arc) segments connected by transition curves.
In a tangent segment the track bed roll angle is typically zero. In the case of railroad track the track roll angle (cant or camber) is typically expressed as the difference in elevation of the two rails, a quantity referred to as the superelevation. A track segment with constant non-zero curvature will typically be superelevated in order to have the component of gravity in the plane of the track provide a majority of the centripetal acceleration inherent in the motion of a vehicle along the curved path so that only a small part of that acceleration needs to be accomplished by lateral force applied to vehicles and passengers or lading. The change of superelevation from zero in a tangent segment to the value selected for the body of a following curve occurs over the length of a transition curve that connects the tangent and the curve proper. Over the length of the transition the curvature of the track will also vary from zero at the end abutting the tangent segment to the value of curvature of the curve body, which is numerically equal to one over the radius of the curve body.
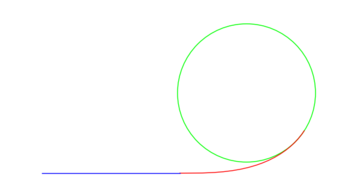
The simplest and most commonly used form of transition curve is that in which the superelevation and horizontal curvature both vary linearly with distance along the track. Cartesian coordinates of points along this spiral are given by the Fresnel integral
Fresnel integral
250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
s. The resulting shape matches a portion of an Euler spiral
Euler spiral
An Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....
, which is also commonly referred to as a clothoid, and sometimes Cornu spiral.
A transition curve can connect a track segment of constant non-zero curvature to another segment with constant curvature that is zero or non-zero of either sign. Successive curves in the same direction are sometimes called progressive curves and successive curves in opposite directions are called reverse curves.
The Euler spiral has two advantages. One is that it is easy for surveyors because the coordinates can be looked up in Fresnel integral
Fresnel integral
250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
tables. The other is that it provides the shortest transition subject to a given limit on the rate of change of the track superelevation (i.e. the twist of the track). However, as has been recognized for a long time, it has undesirable dynamic characteristics due to the large (conceptually infinite) roll acceleration and rate of change of centripetal acceleration at each end. Because of the capabilities of personal computers it is now practical to employ spirals that have dynamics better than those of the Euler spiral.
See also
- Degree of curvatureDegree of curvatureDegree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying....
- Euler spiralEuler spiralAn Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....
- Minimum railway curve radiusMinimum railway curve radiusThe minimum railway curve radius, the shortest design radius, has an important bearing on constructions costs and operating costs and, in combination with superelevation in the case of train tracks, determines the maximum safe speed of a curve. Superelevation is not a factor on tramway tracks...
- Railway systems engineeringRailway systems engineeringRailway systems engineering is a multi-faceted engineering discipline dealing with the design, construction and operation of all types of railway systems....

