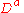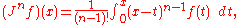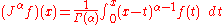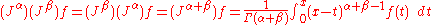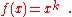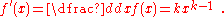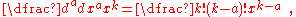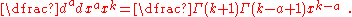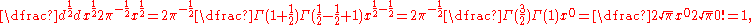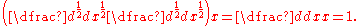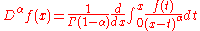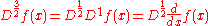
Fractional calculus
Encyclopedia
Fractional calculus is a branch of mathematical analysis
that studies the possibility of taking real number
powers or complex number
powers of the differentiation operator
.
and the integration operator J. (Usually J is used instead of I to avoid confusion with other I-like glyphs and identities
.)
In this context the term powers refers to iterative application or composition, in the same sense that f 2(x) = f(f(x)).
For example, one may ask the question of meaningfully interpreting
as a square root
of the differentiation operator (an operator half iterate), i.e., an expression for some operator that when applied twice to a function will have the same effect as differentiation
. More generally, one can look at the question of defining
for real-number values of a in such a way that when a takes an integer
value n, the usual power of n-fold differentiation is recovered for n > 0, and the −nth power of J when n < 0.
The motivation behind this extension to the differential operator is that the semigroup
of powers Da will form a continuous semigroup with parameter a, inside which the original discrete semigroup of Dn for integer n can be recovered as a subgroup. Continuous semigroups are prevalent in mathematics, and have an interesting theory. Notice here that fraction is then a misnomer for the exponent a, since it need not be rational
; the use of the term fractional calculus is merely conventional.
Fractional differential equations are a generalization of differential equation
s through the application of fractional calculus.
.
As far as the existence of such a theory is concerned, the foundations of the subject were laid by Liouville in a paper from 1832. The fractional derivative of a function to order a is often now defined by means of the Fourier
or Mellin
integral transforms.
, or half-derivative, such that
It turns out that there is such an operator, and indeed for any
, there exists an operator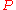 
such that
or to put it another way, the definition of
can be extended to all real values of n.
To delve into a little detail, start with the Gamma function
, which extends factorial
s to non-integer values.
This is defined such that
Assuming a function
that is defined where 
, form the definite integral from 0 to x. Call this
Repeating this process gives
and this can be extended arbitrarily.
The Cauchy formula for repeated integration
, namely
leads to a straightforward way to a generalization for real n.
Simply using the Gamma function to remove the discrete nature of the factorial function (recalling that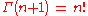
, or equivalently 
) gives us a natural candidate for fractional applications of the integral operator.
This is in fact a well-defined operator.
It can be shown that the J operator satisfies
this relationship is called the semigroup property of fractional differintegral operators. Unfortunately the comparable process for the derivative operator D is significantly more complex, but it can be shown that D is neither commutative nor additive
in general.
Let us assume that 
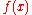is a monomial of the form
The first derivative is as usual
Repeating this gives the more general result that
Which, after replacing the factorial
s with the Gamma function
, leads us to
For
and 
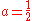, we obtain the half-derivative of the function 
as
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
that studies the possibility of taking real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
powers or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
powers of the differentiation operator
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
.
and the integration operator J. (Usually J is used instead of I to avoid confusion with other I-like glyphs and identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
.)
In this context the term powers refers to iterative application or composition, in the same sense that f 2(x) = f(f(x)).
For example, one may ask the question of meaningfully interpreting
as a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the differentiation operator (an operator half iterate), i.e., an expression for some operator that when applied twice to a function will have the same effect as differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. More generally, one can look at the question of defining
for real-number values of a in such a way that when a takes an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
value n, the usual power of n-fold differentiation is recovered for n > 0, and the −nth power of J when n < 0.
The motivation behind this extension to the differential operator is that the semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
of powers Da will form a continuous semigroup with parameter a, inside which the original discrete semigroup of Dn for integer n can be recovered as a subgroup. Continuous semigroups are prevalent in mathematics, and have an interesting theory. Notice here that fraction is then a misnomer for the exponent a, since it need not be rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
; the use of the term fractional calculus is merely conventional.
Fractional differential equations are a generalization of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s through the application of fractional calculus.
Nature of the fractional derivative
An important point is that the fractional derivative at a point x is a local property only when a is an integer; in non-integer cases we cannot say that the fractional derivative at x of a function f depends only on the graph of f very near x, in the way that integer-power derivatives certainly do. Therefore it is expected that the theory involves some sort of boundary conditions, involving information on the function further out. To use a metaphor, the fractional derivative requires some peripheral visionPeripheral vision
Peripheral vision is a part of vision that occurs outside the very center of gaze. There is a broad set of non-central points in the field of view that is included in the notion of peripheral vision...
.
As far as the existence of such a theory is concerned, the foundations of the subject were laid by Liouville in a paper from 1832. The fractional derivative of a function to order a is often now defined by means of the Fourier
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or Mellin
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
integral transforms.
Heuristics
A fairly natural question to ask is whether there exists an operator, or half-derivative, such that-
.
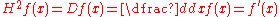It turns out that there is such an operator, and indeed for any
, there exists an operator 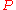such that-
,
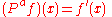or to put it another way, the definition of
can be extended to all real values of n.To delve into a little detail, start with the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, which extends factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s to non-integer values.
This is defined such that
-
.
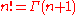Assuming a function
that is defined where , form the definite integral from 0 to x. Call this-
.
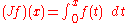Repeating this process gives
-
,
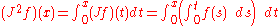and this can be extended arbitrarily.
The Cauchy formula for repeated integration
Cauchy formula for repeated integration
The Cauchy formula for repeated integration, named after Augustin Louis Cauchy, allows one to compress n antidifferentiations of a function into a single integral .-Scalar case:Let ƒ be a continuous function on the real line...
, namely
leads to a straightforward way to a generalization for real n.
Simply using the Gamma function to remove the discrete nature of the factorial function (recalling that
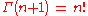, or equivalently ) gives us a natural candidate for fractional applications of the integral operator.
This is in fact a well-defined operator.
It can be shown that the J operator satisfies
this relationship is called the semigroup property of fractional differintegral operators. Unfortunately the comparable process for the derivative operator D is significantly more complex, but it can be shown that D is neither commutative nor additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
in general.
Fractional derivative of a simple function
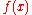is a monomial of the form
The first derivative is as usual
Repeating this gives the more general result that
Which, after replacing the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s with the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, leads us to
For
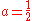and , we obtain the half-derivative of the function as-
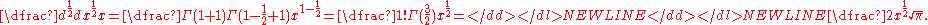
Repeating this process yields
which is indeed the expected result of
This extension of the above differential operator need not be constrained only to real powers. For example, the
th derivative of the 
th derivative yields the 2nd derivative. Also notice that setting negative values for a yields integrals.
The complete fractional derivative which will yield the same result as above is (for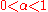
)
For arbitrary
, since the gamma function is undefined for arguments whose real part is a negative integer, it is necessary to apply the fractional derivative after the integer derivative has been performed. For example,
Laplace transform
We can also come at the question via the Laplace transform. Noting that
and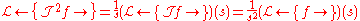
etc., we assert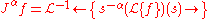
.
For example
as expected. Indeed, given the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
rule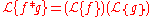
(and shorthanding 
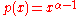for clarity) we find that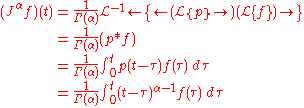
which is what Cauchy gave us above.
Laplace transforms "work" on relatively few functions, but they are often useful for solving fractional differential equations.
Riemann–Liouville fractional integral
The classical form of fractional calculus is given by the Riemann–Liouville integral, essentially what has been described above. The theory for periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s, therefore including the 'boundary condition' of repeating after a period, is the Weyl integral. It is defined on Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, and requires the constant Fourier coefficient to vanish (so, applies to functions on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
integrating to 0).
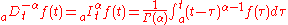
By contrast the Grünwald–Letnikov derivative starts with the derivative instead of the integral.
Riemann–Liouville fractional derivative
The corresponding derivative is calculated using Lagrange's rule for differential operators. Computing n-th order derivative over the integral of order n-α, the α order derivative is obtained. Is important to remark that n is the nearest integer bigger than α.
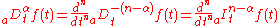
Caputo fractional derivative
There is another option for computing fractional derivatives, the Caputo fractional derivative was introduced by M. Caputo in 1990, In contrast to the Riemann Liouville fractional derivative, when solving differential equations using Caputo definition is not necessary to define fractional order initial conditions. Caputo's definition is illustrated as follows.
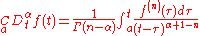
Functional calculus
In the context of functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, functions f(D) more general than powers are studied in the functional calculusFunctional calculusIn mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
of spectral theorySpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. The theory of pseudo-differential operatorPseudo-differential operatorIn mathematical analysis a pseudo-differential operator is an extension of the concept of differential operator. Pseudo-differential operators are used extensively in the theory of partial differential equations and quantum field theory....
s also allows one to consider powers of D. The operators arising are examples of singular integral operators; and the generalisation of the classical theory to higher dimensions is called the theory of Riesz potentialRiesz potentialIn mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space...
s. So there are a number of contemporary theories available, within which fractional calculus can be discussed. See also Erdélyi–Kober operator, important in special function theory , .
Fractional Conservation of Mass
As described by Wheatcraft and Meerschaert (2008), a fractional conservation of mass equation is needed when the control volume is not large enough compared to the scale of heterogeneity and when the flux within the control volume is non-linear. In the referenced paper, the fractional conservation of mass equation for fluid flow is:
Fractional Advection Dispersion Equation
This equation has been shown useful for modeling contaminant flow in heterogenous porous media.
WKB approximation
For the semiclassical approximation in one dimensional spatial system (x,t) the inverse of the potential
inside the Hamiltonian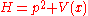 
is given by the half-integral of the density of states 
taken in units where 
(ref: 6)
Structural damping models
Fractional derivatives are used to model viscoelastic dampingDampingIn physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
in certain types of materials like polymers.
See also
- Differintegral
- Fractional dynamicsFractional dynamicsFractional dynamics is a field of study in physics, mechanics, mathematics, and economics investigating the behavior of objects and systems that are described byusing integrations and differentiation of fractional orders, by methods of fractional calculus....
- Fractional Fourier transformFractional Fourier transformIn mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
- NeopolarogramNeopolarogramThe term Neopolarogram refers to mathematical derivatives of polarograms or cyclic voltammograms that in effect deconvolute diffusion and electrochemical kinetics. This is achieved by analog or digital implementations of fractional calculus. The implementation of fractional derivative calculations...
External links
- Eric W. Weisstein. "Fractional Differential Equation." From MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
— A Wolfram Web Resource. - MathWorld - Fractional calculus
- MathWorld - Fractional derivative
- Fractional Calculus at MathPages
- Specialized journal: Fractional Calculus and Applied Analysis
- Specialized journal: Fractional Differential Equations (FDE)
- Specialized journal: Communications in Fractional Calculus (ISSN 2218-3892)
- www.nasatech.com
- unr.edu (Broken Link)
- Igor Podlubny's collection of related books, articles, links, software, etc.
- GigaHedron - Richard Herrmann's collection of books, articles, preprints, etc.
- s.dugowson.free.fr
- History, Definitions, and Applications for the Engineer (PDF), by Adam Loverro, University of Notre DameUniversity of Notre DameThe University of Notre Dame du Lac is a Catholic research university located in Notre Dame, an unincorporated community north of the city of South Bend, in St. Joseph County, Indiana, United States...
- Fractional Calculus Modelling
- Introductory Notes on Fractional Calculus
- Pseudodifferential operators and diffusive representation in modeling, control and signal
-
