
Fractional Fourier transform
Encyclopedia
In mathematics
, in the area of harmonic analysis
, the fractional Fourier transform (FRFT) is a linear transformation
generalizing the Fourier transform
. It can be thought of as the Fourier transform to the n-th power where n need not be an integer
— thus, it can transform a function to an intermediate domain between time and frequency
. Its applications range from filter design
and signal analysis to phase retrieval
and pattern recognition
.
The FRFT can be used to define fractional convolution
, correlation
, and other operations, and can also be further generalized into the linear canonical transformation
(LCT). An early definition of the FRFT was given by Namias, but it was not widely recognized until it was independently reinvented around 1993 by several groups of researchers. Since then, there has been a surge of interest in extending Shannon's sampling theorem
for signals which are bandlimited in Fractional Fourier domain.
A completely different meaning for "fractional Fourier transform" was introduced by Bailey and Swartztrauber as essentially another name for a z-transform
, and in particular for the case that corresponds to a discrete Fourier transform
shifted by a fractional amount in frequency space (multiplying the input by a linear chirp
) and evaluating at a fractional set of frequency points (e.g. considering only a small portion of the spectrum). (Such transforms can be evaluated efficiently by Bluestein's FFT algorithm
.) This terminology has fallen out of use in most of the technical literature, however, in preference to the FRFT. The remainder of this article describes the FRFT.
See also the chirplet transform
for a related generalization of the Fourier transform
.
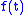 is denoted by
is denoted by 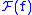 , then
, then 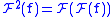 , and in general
, and in general 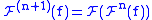 ; similarly,
; similarly,  denotes the n-th power of the inverse transform
denotes the n-th power of the inverse transform 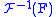 of
of  . The FRFT further extends this definition to handle non-integer powers
. The FRFT further extends this definition to handle non-integer powers 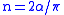 for any real
for any real
 , denoted by
, denoted by 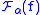 and having the properties:
and having the properties:
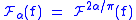
when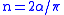 is an integer, and:
is an integer, and:
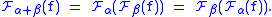
More specifically,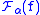 is given by the equation:
is given by the equation:
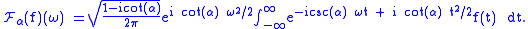
Note that, for , this becomes precisely the definition of the continuous Fourier transform, and for
, this becomes precisely the definition of the continuous Fourier transform, and for  it is the definition of the inverse continuous Fourier transform.
it is the definition of the inverse continuous Fourier transform.
If is an integer multiple of
is an integer multiple of  , then the cotangent and cosecant functions above diverge. However, this can be handled by taking the limit
, then the cotangent and cosecant functions above diverge. However, this can be handled by taking the limit
, and leads to a Dirac delta function
in the integrand. More easily, since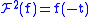 ,
, 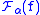 must be simply
must be simply 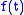 or
or 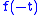 for
for  an even or odd
an even or odd
multiple of , respectively.
, respectively.
.
The discrete fractional Fourier transform is defined by Zeev Zalevsky
in
and
.
Wavelet–fractional Fourier transforms: uses other orthonormal bases for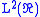 instead of Hermite–Gaussian functions. The new orthonormal basis is derivated from multiresolution analysis and orthonormal wavelets.
instead of Hermite–Gaussian functions. The new orthonormal basis is derivated from multiresolution analysis and orthonormal wavelets.
. There is also a fractional Radon transform, a symplectic
FRFT, and a symplectic wavelet transform. Because quantum circuit
s are based on unitary operations, they are useful for computing integral transforms as the latter are unitary operators on a function space
. A quantum circuit has been designed which implements the FRFT.
, which generalizes the fractional Fourier transform and allows linear transforms of the time-frequency domain other than rotation.
Take the below figure as an example. If the signal in the time domain is rectangular (as below), it will become a sinc function in the frequency domain. But if we apply the fractional Fourier transform to the rectangular signal, the transformation output will be in the domain between time and frequency.
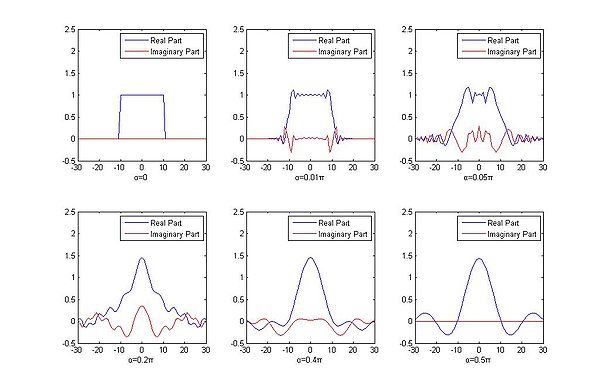
Actually, fractional Fourier transform is a rotation operation on the time frequency distribution. From the definition above, for α = 0, there will be no change after applying fractional Fourier transform, and for α = π/2, fractional Fourier transform becomes a Fourier transform, which rotates the time frequency distribution with π/2. For other value of α, fractional Fourier transform rotates the time frequency distribution according to α. The following figure shows the results of the fractional Fourier transform with different values of α.
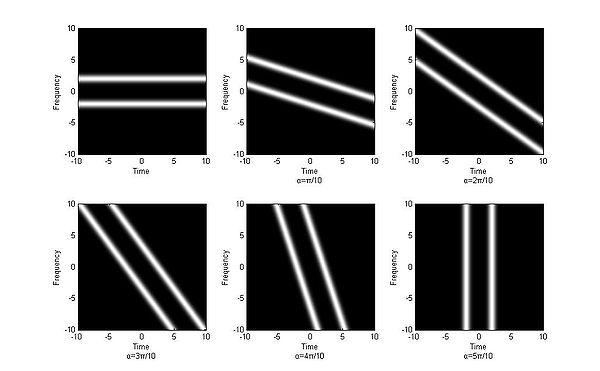
. It is useful to filter noise, but with the condition that it does not overlap with the desired signal in the time frequency domain. Consider the following example. We cannot apply a filter directly to eliminate the noise, but with the help of the fractional Fourier transform, we can rotate the signal (including the desired signal and noise) first. We then apply a specific filter which will allow only the desired signal to pass. Thus the noise will be removed completely. Then we use the fractional Fourier transform again to rotate the signal back and we can get the desired signal.
 Thus, using just truncation in the time domain, or equivalently low-pass filter
Thus, using just truncation in the time domain, or equivalently low-pass filter
s in the frequency domain, one can cut out any convex set
in time-frequency space; just using time domain or frequency domain methods without fractional Fourier transforms only allow cutting out rectangles parallel to the axes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, the fractional Fourier transform (FRFT) is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
generalizing the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. It can be thought of as the Fourier transform to the n-th power where n need not be an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
— thus, it can transform a function to an intermediate domain between time and frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. Its applications range from filter design
Filter design
Filter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
and signal analysis to phase retrieval
Phase retrieval
Phase retrieval concerns the solution to the phase problem. Given a complex signal F, of amplitude |F|, and phase \phi:phase retrieval consists in finding the phase that for a measured amplitude satisfies a set of constraints....
and pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
.
The FRFT can be used to define fractional convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
, correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, and other operations, and can also be further generalized into the linear canonical transformation
Linear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
(LCT). An early definition of the FRFT was given by Namias, but it was not widely recognized until it was independently reinvented around 1993 by several groups of researchers. Since then, there has been a surge of interest in extending Shannon's sampling theorem
for signals which are bandlimited in Fractional Fourier domain.
A completely different meaning for "fractional Fourier transform" was introduced by Bailey and Swartztrauber as essentially another name for a z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
, and in particular for the case that corresponds to a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
shifted by a fractional amount in frequency space (multiplying the input by a linear chirp
Chirp
A chirp is a signal in which the frequency increases or decreases with time. In some sources, the term chirp is used interchangeably with sweep signal. It is commonly used in sonar and radar, but has other applications, such as in spread spectrum communications...
) and evaluating at a fractional set of frequency points (e.g. considering only a small portion of the spectrum). (Such transforms can be evaluated efficiently by Bluestein's FFT algorithm
Bluestein's FFT algorithm
Bluestein's FFT algorithm , commonly called the chirp z-transform algorithm , is a fast Fourier transform algorithm that computes the discrete Fourier transform of arbitrary sizes by re-expressing the DFT as a convolution...
.) This terminology has fallen out of use in most of the technical literature, however, in preference to the FRFT. The remainder of this article describes the FRFT.
See also the chirplet transform
Chirplet transform
In signal processing, the chirplet transform is an inner product of an input signal with a family of analysis primitives called chirplets.-Similarity to other transforms:...
for a related generalization of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
Definition
If the continuous Fourier transform of a function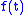 is denoted by
is denoted by 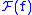 , then
, then 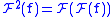 , and in general
, and in general 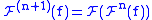 ; similarly,
; similarly,  denotes the n-th power of the inverse transform
denotes the n-th power of the inverse transform 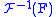 of
of  . The FRFT further extends this definition to handle non-integer powers
. The FRFT further extends this definition to handle non-integer powers 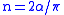 for any real
for any realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 , denoted by
, denoted by 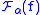 and having the properties:
and having the properties: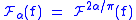
when
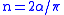 is an integer, and:
is an integer, and: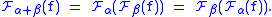
More specifically,
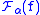 is given by the equation:
is given by the equation: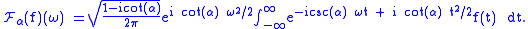
Note that, for
 , this becomes precisely the definition of the continuous Fourier transform, and for
, this becomes precisely the definition of the continuous Fourier transform, and for  it is the definition of the inverse continuous Fourier transform.
it is the definition of the inverse continuous Fourier transform.If
 is an integer multiple of
is an integer multiple of  , then the cotangent and cosecant functions above diverge. However, this can be handled by taking the limit
, then the cotangent and cosecant functions above diverge. However, this can be handled by taking the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, and leads to a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
in the integrand. More easily, since
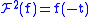 ,
, 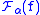 must be simply
must be simply 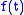 or
or 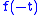 for
for  an even or odd
an even or oddEven and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
multiple of
 , respectively.
, respectively.Related transforms
There also exist related fractional generalizations of similar transforms such as the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
The discrete fractional Fourier transform is defined by Zeev Zalevsky
Zeev Zalevsky
Zeev Zalevsky ; was born in the Russian SFSR in the Soviet Union in 1971 and came with his family to Israel. Zalevsky is an Israeli physicist specializing in Optoelectronics. He is a Professor of Electrical engineering and Nanophotonics at Bar Ilan University in Ramat Gan, Israel...
in
and
.
Wavelet–fractional Fourier transforms: uses other orthonormal bases for
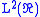 instead of Hermite–Gaussian functions. The new orthonormal basis is derivated from multiresolution analysis and orthonormal wavelets.
instead of Hermite–Gaussian functions. The new orthonormal basis is derivated from multiresolution analysis and orthonormal wavelets.Generalization
The Fourier transform is essentially bosonic; it works because it is consistent with the superposition principle and related interference patterns. There is also a fermionic Fourier transform. These have been generalized into a supersymmetric FRFT, and a supersymmetric Radon transformRadon transform
thumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
. There is also a fractional Radon transform, a symplectic
Time-frequency analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations...
FRFT, and a symplectic wavelet transform. Because quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
s are based on unitary operations, they are useful for computing integral transforms as the latter are unitary operators on a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. A quantum circuit has been designed which implements the FRFT.
Interpretation of the fractional Fourier transform
The usual interpretation of the Fourier transform is as a transformation of a time domain signal into a frequency domain signal. On the other hand, the interpretation of the inverse Fourier transform is as a transformation of a frequency domain signal into a time domain signal. Apparently, fractional Fourier transforms can transform a signal (either in the time domain or frequency domain) into the domain between time and frequency: it is a rotation in the time-frequency domain. This perspective is generalized by the linear canonical transformationLinear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
, which generalizes the fractional Fourier transform and allows linear transforms of the time-frequency domain other than rotation.
Take the below figure as an example. If the signal in the time domain is rectangular (as below), it will become a sinc function in the frequency domain. But if we apply the fractional Fourier transform to the rectangular signal, the transformation output will be in the domain between time and frequency.

Actually, fractional Fourier transform is a rotation operation on the time frequency distribution. From the definition above, for α = 0, there will be no change after applying fractional Fourier transform, and for α = π/2, fractional Fourier transform becomes a Fourier transform, which rotates the time frequency distribution with π/2. For other value of α, fractional Fourier transform rotates the time frequency distribution according to α. The following figure shows the results of the fractional Fourier transform with different values of α.

Application
Fractional Fourier transform can be used in time frequency analysis and DSPDigital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
. It is useful to filter noise, but with the condition that it does not overlap with the desired signal in the time frequency domain. Consider the following example. We cannot apply a filter directly to eliminate the noise, but with the help of the fractional Fourier transform, we can rotate the signal (including the desired signal and noise) first. We then apply a specific filter which will allow only the desired signal to pass. Thus the noise will be removed completely. Then we use the fractional Fourier transform again to rotate the signal back and we can get the desired signal.

Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
s in the frequency domain, one can cut out any convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in time-frequency space; just using time domain or frequency domain methods without fractional Fourier transforms only allow cutting out rectangles parallel to the axes.
See also
Other time-frequency transforms:- Linear canonical transformationLinear canonical transformationIn Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
- short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
- wavelet transform
- chirplet transformChirplet transformIn signal processing, the chirplet transform is an inner product of an input signal with a family of analysis primitives called chirplets.-Similarity to other transforms:...
External links
- DiscreteTFDs -- software for computing the fractional Fourier transform and time-frequency distributions
- "Fractional Fourier Transform" by Enrique Zeleny, The Wolfram Demonstrations Project.
- Dr YangQuan Chen's FRFT (Fractional Fourier Transform) Webpages

