
Differintegral
Encyclopedia
In fractional calculus
, an area of applied mathematics
, the differintegral is a combined differentiation
/integration operator. Applied to a function
ƒ, the q-differintegral of f, here denoted by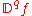
is the fractional derivative (if q>0) or fractional integral (if q<0). If q=0, then the q-th differintegral of a function is the function itself. In the context of fractional integration and differentiation, there are several legitimate definitions of the differintegral.
, here denoted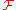 :
:
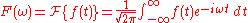
Using the continuous Fourier transform, in Fourier space, differentiation transforms into a multiplication:
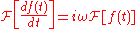
So,
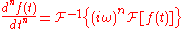
which generalizes to

Under the Laplace transform, here denoted by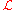 , differentiation transforms into a multiplication
, differentiation transforms into a multiplication
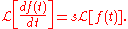
Generalizing to arbitrary order and solving for Dqf(t), one obtains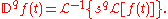

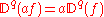
Zero rule
Product rule
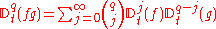
In general, composition (or semigroup
) rule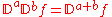
is not satisfied. See Property 2.4 (page 75) in the book A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, 2006).
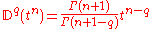
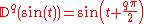
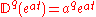
Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
, an area of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, the differintegral is a combined differentiation
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
/integration operator. Applied to a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ƒ, the q-differintegral of f, here denoted by
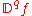
is the fractional derivative (if q>0) or fractional integral (if q<0). If q=0, then the q-th differintegral of a function is the function itself. In the context of fractional integration and differentiation, there are several legitimate definitions of the differintegral.
Standard definitions
The three most common forms are:- This is the simplest and easiest to use, and consequently it is the most often used. It is a generalization of the Cauchy formula for repeated integrationCauchy formula for repeated integrationThe Cauchy formula for repeated integration, named after Augustin Louis Cauchy, allows one to compress n antidifferentiations of a function into a single integral .-Scalar case:Let ƒ be a continuous function on the real line...
to arbitrary order.
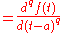
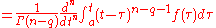
- The Grunwald-Letnikov differintegralGrunwald-Letnikov differintegralIn mathematics, the Grünwald–Letnikov derivative is a basic extension of the derivative in fractional calculus, that allows one to take the derivative a non-integer number of times...
- The Grunwald-Letnikov differintegral is a direct generalization of the definition of a derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. It is more difficult to use than the Riemann-Liouville differintegral, but can sometimes be used to solve problems that the Riemann-Liouville cannot.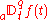
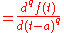
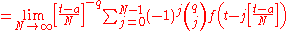
- The Weyl differintegralWeyl differintegralIn mathematics, the Weyl integral is an operator defined, as an example of fractional calculus, on functions f on the unit circle having integral 0 and a Fourier series. In other words there is a Fourier series for f of the form...
- This is formally similar to the Riemann-Liouville differintegral, but applies to periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s, with integral zero over a period.
Definitions via transforms
Recall the continuous Fourier transformContinuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
, here denoted
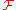 :
: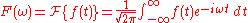
Using the continuous Fourier transform, in Fourier space, differentiation transforms into a multiplication:
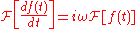
So,
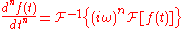
which generalizes to

Under the Laplace transform, here denoted by
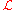 , differentiation transforms into a multiplication
, differentiation transforms into a multiplication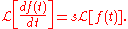
Generalizing to arbitrary order and solving for Dqf(t), one obtains
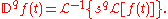
Basic formal properties
Linearity rules
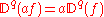
Zero rule

Product rule
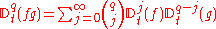
In general, composition (or semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
) rule
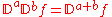
is not satisfied. See Property 2.4 (page 75) in the book A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, 2006).
Some basic formulae
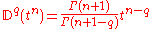
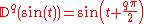
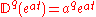
External links
- MathWorld - Fractional calculus
- MathWorld - Fractional derivative
- Specialized journal: Fractional Calculus and Applied Analysis
- Specialized journal: Fractional Dynamic Systems (FDS)
- Specialized journal: Communications in Fractional Calculus (ISSN 2218-3892)
- http://www.nasatech.com/Briefs/Oct02/LEW17139.html
- http://unr.edu/homepage/mcubed/FRG.html
- Igor Podlubny's collection of related books, articles, links, software, etc.
- Podlubny, I., Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus and Applied Analysis, vol. 5, no. 4, 2002, 367–386. (available as original article, or preprint at Arxiv.org)

