Fokker periodicity blocks
Encyclopedia
Fokker periodicity blocks are a concept in tuning theory used to mathematically relate musical intervals in just intonation
to those in equal tuning
. They are named after Adriaan Daniël Fokker
. These are included as the primary subset of what Erv Wilson
refers to as constant structures, where "each interval occurs always subtended by the same number of steps".
The basic idea of Fokker's periodicity blocks is to represent just ratios as points on a lattice
, to find vectors
in the lattice which represent very small intervals, known as commas
. Treating pitches separated by a comma as equivalent "folds" the lattice, effectively reducing its dimension by one. For an n-dimensional lattice, identifying n commas (as long as they are linearly independent) reduces the dimension of the lattice to zero, meaning that the number of pitches in the lattice is finite. This zero-dimensional lattice is a periodicity block. Identifying the m pitches of the periodicity block with m-equal tuning gives equal tuning approximations of the just ratios that defined the original lattice.
Note that octaves are usually ignored in constructing periodicity blocks (as they are in scale theory generally) because it is assumed that for any pitch in the tuning system, all pitches differing from it by some number of octaves are also available in principle. In other words, all pitches and intervals can be considered as residues modulo octave. This simplification is commonly known as octave equivalence.
(i.e. grid) embedded in n-space have a numerical value assigned to each of its nodes. Let n be preferably equal either to 1, 2, or 3. In the two-dimensional case, the lattice is a square lattice
. In the 3-D case, the lattice is cubic.
Examples of such lattices are the following (x, y, z and w are integer
s):
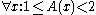
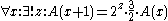
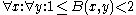
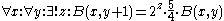
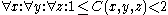
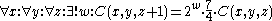
Find n nodes on the lattice other than the origin such that their values are sufficiently close to either 1 or 2.
Vectors from the origin to each one of these special nodes are called unison vectors. A quantity n of unison vectors are enough to define an n-dimensional tiling
pattern. Let the n unison vectors define the sides of a tile. In 1-D, a tile is a line segment
. In 2-D, a tile is a parallelogram
. In 3-D, a tile is a parallelepiped
.
Each tile has an area given by the absolute value of the determinant
of the matrix of unison vectors: i.e. in the 2-D case if the unison vectors are u and v, such that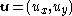
and 
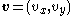then the area of a 2-D tile is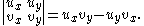
Each tile is called a Fokker periodicity block. The area of each block is always a natural number
equal to the number of nodes falling within each block.
, the distance by which three just major thirds fall short of an octave, about 41 cents) and 81/80 (the syntonic comma
, the difference between four perfect fifths and a just major third, about 21.5 cents). The result is a block of twelve, showing how twelve-tone equal temperament
approximates the ratios of the 5-limit
.
Example 2: However, if we were to reject the diesis as a unison vector and instead choose the difference between five major thirds (minus an octave) and a fourth, 3125/3072 (about 30 cents), the result is a block of 19, showing how 19-TET approximates ratios of the 5-limit.
Example 3: In the 3-dimensional lattice of perfect fifths, just major thirds, and just minor sevenths (ratio 7/4), the identification of the syntonic comma, the septimal kleisma
(225/224, about 8 cents), and the ratio 1029/1024 (the difference between three septimal whole tones and a fourth, about 8.4 cents) results in a block of 31, showing how 31-TET approximates ratios of the 7-limit.
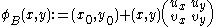
which is really a linear combination
:
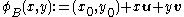
where point (x0, y0) can be any point, preferably not a node of the primary lattice, and preferably so that points φ(0,1), φ(1,0) and φ(1,1) are not any nodes either.
Then membership of primary nodes within periodicity blocks may be tested analytically through the inverse φ function: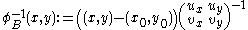
Let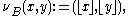
then let the pitch B(x,y) belong to the scale MB iff
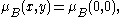i.e.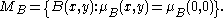
For the one-dimensional case: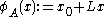
where L is the length of the unison vector,
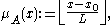
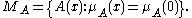
For the three-dimensional case,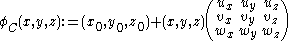
where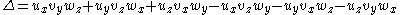
is the determinant of the matrix of unison vectors.
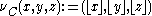
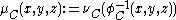
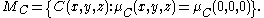
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
to those in equal tuning
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
. They are named after Adriaan Daniël Fokker
Adriaan Fokker
Adriaan Daniël Fokker , was a Dutch physicist and musician.Fokker was born in Buitenzorg, Dutch East Indies ; he was a cousin of the aeronautical engineer Anthony Fokker...
. These are included as the primary subset of what Erv Wilson
Erv Wilson
Ervin Wilson is a Mexican/American music theorist. Despite his avoidance of academia, Wilson has been influential on those interested in microtonal music and just intonation, especially in the areas of scale, keyboard, and notation design...
refers to as constant structures, where "each interval occurs always subtended by the same number of steps".
The basic idea of Fokker's periodicity blocks is to represent just ratios as points on a lattice
Lattice (music)
In musical tuning, a lattice "is a way of modeling the tuning relationships in a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio...
, to find vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in the lattice which represent very small intervals, known as commas
Comma (music)
In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word "comma" used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning...
. Treating pitches separated by a comma as equivalent "folds" the lattice, effectively reducing its dimension by one. For an n-dimensional lattice, identifying n commas (as long as they are linearly independent) reduces the dimension of the lattice to zero, meaning that the number of pitches in the lattice is finite. This zero-dimensional lattice is a periodicity block. Identifying the m pitches of the periodicity block with m-equal tuning gives equal tuning approximations of the just ratios that defined the original lattice.
Note that octaves are usually ignored in constructing periodicity blocks (as they are in scale theory generally) because it is assumed that for any pitch in the tuning system, all pitches differing from it by some number of octaves are also available in principle. In other words, all pitches and intervals can be considered as residues modulo octave. This simplification is commonly known as octave equivalence.
Definition of periodicity blocks
Let an n-dimensional latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
(i.e. grid) embedded in n-space have a numerical value assigned to each of its nodes. Let n be preferably equal either to 1, 2, or 3. In the two-dimensional case, the lattice is a square lattice
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
. In the 3-D case, the lattice is cubic.
Examples of such lattices are the following (x, y, z and w are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s):
- One-dimensional: 3-limitLimit (music)In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
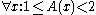
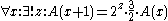
- Two-dimensional: 5-limit
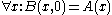
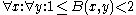
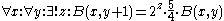
- Three-dimensional: 7-limit
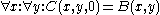
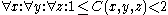
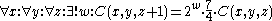
Find n nodes on the lattice other than the origin such that their values are sufficiently close to either 1 or 2.
Vectors from the origin to each one of these special nodes are called unison vectors. A quantity n of unison vectors are enough to define an n-dimensional tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
pattern. Let the n unison vectors define the sides of a tile. In 1-D, a tile is a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
. In 2-D, a tile is a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
. In 3-D, a tile is a parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
.
Each tile has an area given by the absolute value of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix of unison vectors: i.e. in the 2-D case if the unison vectors are u and v, such that
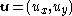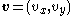and then the area of a 2-D tile is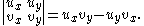Each tile is called a Fokker periodicity block. The area of each block is always a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
equal to the number of nodes falling within each block.
Examples
Example 1: Take the 2-dimensional lattice of perfect fifths (ratio 3/2) and just major thirds (ratio 5/4). Choose the commas 128/125 (the diesisDiesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
, the distance by which three just major thirds fall short of an octave, about 41 cents) and 81/80 (the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, the difference between four perfect fifths and a just major third, about 21.5 cents). The result is a block of twelve, showing how twelve-tone equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
approximates the ratios of the 5-limit
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
.
Example 2: However, if we were to reject the diesis as a unison vector and instead choose the difference between five major thirds (minus an octave) and a fourth, 3125/3072 (about 30 cents), the result is a block of 19, showing how 19-TET approximates ratios of the 5-limit.
Example 3: In the 3-dimensional lattice of perfect fifths, just major thirds, and just minor sevenths (ratio 7/4), the identification of the syntonic comma, the septimal kleisma
Septimal kleisma
In music, the ratio 225/224 is called the septimal kleisma .It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 2 . That says that it is the amount that two major thirds of 5/4 and a septimal...
(225/224, about 8 cents), and the ratio 1029/1024 (the difference between three septimal whole tones and a fourth, about 8.4 cents) results in a block of 31, showing how 31-TET approximates ratios of the 7-limit.
Mathematical characteristics of periodicity blocks
The periodicity blocks form a secondary, oblique lattice, superimposed on the first one. This lattice may be given by a function φ: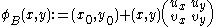which is really a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
:
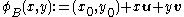
where point (x0, y0) can be any point, preferably not a node of the primary lattice, and preferably so that points φ(0,1), φ(1,0) and φ(1,1) are not any nodes either.
Then membership of primary nodes within periodicity blocks may be tested analytically through the inverse φ function:
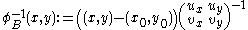
Let
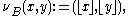
then let the pitch B(x,y) belong to the scale MB iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
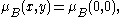i.e.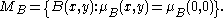For the one-dimensional case:
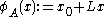
where L is the length of the unison vector,
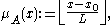
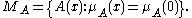
For the three-dimensional case,
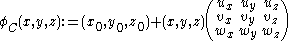
where
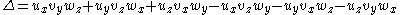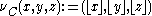
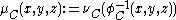
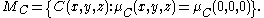
is the determinant of the matrix of unison vectors.External links
- Fokker, A. D., (n.d.), Unison Vectors and Periodicity Blocks in the Three-Dimensional (3-5-7-) Lattice of Notes
- Paul Erlich, (1999), A Gentle Introduction to Fokker Periodicity Blocks: Part 1; Part 2; etc.