
Comma (music)
Encyclopedia
In music theory
, a comma is a minute interval
, the difference resulting from tuning
one note two different ways. The word "comma" used without qualification refers to the syntonic comma
, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning
system, and another F tuned using the D-based quarter-comma meantone
system. Even within the same tuning system, when scales with more than 12 notes are built, two notes which should coincide may have a different tuning. For example, in extended scales produced with 5-limit tuning an A tuned as a major third
below C5 and a G tuned as two major thirds above C4 will not be exactly the same note, as they would be in equal temperament
. The difference between those notes, the diesis
, also known as lesser diesis, is more than 40% of a semitone
, and is easily audible.
Commas are often defined as the difference in size between two semitone
s, even within a single non-extended 12-tone scale
. Each meantone temperament
tuning system produces a 12-tone scale characterized by two different kinds of semitones (diatonic and chromatic), and hence by a comma of unique size. The same is true for Pythagorean tuning.
In just intonation
, more than two kinds of semitones may be produced. Thus, a single tuning system may be characterized by several different commas. For instance, a commonly used version of 5-limit tuning produces a 12-tone scale with four kinds of semitones and four commas.
The size of commas is commonly expressed and compared in terms of cents
– 1/1200 fractions of an octave
on a logarithm
ic scale.
s", m2 is the minor second (diatonic semitone), A1 is the augmented unison (chromatic semitone), and S1, S2, S3, S4 are semitones as defined here. In the columns labeled "Interval
1" and "Interval 2", all intervals are presumed to be tuned in just intonation
. Notice that the Pythagorean comma
(PC) and the syntonic comma
(SC) are basic intervals which can be used as yardsticks to define some of the other commas. For instance, the difference between them is a small comma called schisma
. A schisma is not audible in many contexts, as its size is narrower than the smallest noticeable difference
between tones (which is around six cents).
The syntonic comma has a crucial role in the history of music. It is the amount by which some of the notes produced in Pythagorean tuning were flattened or sharpened to produce just minor and major thirds. In Pythagorean tuning, the only highly consonant intervals were the perfect fifth
and its inversion, the perfect fourth
. The Pythagorean major third (81:64) and minor third (32:27) were dissonant
, and this prevented musicians from freely using triad
s and chord
s, forcing them to write music with relatively simple texture
. In late Middle Ages
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated
ratio of
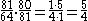
and at the same time E-G is sharpened to the just ratio of
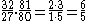
This brought to the creation of a new tuning system, known as quarter-comma meantone
, which permitted the full development of music with complex texture
, such as polyphonic music
, or melodies with instrumental accompaniment
. Since then, other tuning systems were developed, and the syntonic comma was used as a reference value to temper the perfect fifths in an entire family of them. Namely, in the family belonging to the syntonic temperament
continuum, including meantone temperament
s.
, and any kind of meantone temperament
tuning system which tempers the fifth to a size smaller than 700 cents, the comma can be equivalently defined as:
In Pythagorean tuning, and any kind of meantone temperament
tuning system which tempers the fifth to a size larger than 700 cents (such as 1/12-comma meantone), the comma is the opposite of the above mentioned differences. For instance, the Pythagorean comma is the opposite of a Pythagorean diminished second, i.e. it is the difference between chromatic semitone and diatonic semitone, rather than vice versa.
In each of the above mentioned tuning systems, these differences have all the same size. For instance, in Pythagorean tuning they are all equal to the opposite of a Pythagorean comma
, and in quarter-comma meantone they are all equal to a diesis
.
and Wolfgang von Schweinitz
worked together in Berlin to develop a method to exactly indicate pitches in staff notation. This method was called the extended Helmholtz-Ellis JI
pitch notation. Sabat and Schweinitz take the "conventional" flats, naturals and sharps as a Pythagorean series of perfect fifths. Thus, a series of perfect fifths beginning with F proceeds C G D A E B F# and so on. The advantage for musicians is that conventional reading of the basic fourths and fifths remains familiar. Such an approach has also been advocated by Daniel James Wolf
and by Joe Monzo, who refers to it by the acronym HEWM (Helmholtz-Ellis-Wolf-Monzo). In the Sabat-Schweinitz design, syntonic commas are marked by arrows attached to the flat, natural or sharp sign, septimal commas using Giuseppe Tartini's symbol, and undecimal quartertones using the common practice quartertone signs (a single cross and backwards flat). For higher primes, additional signs have been designed. To facilitate quick estimation of pitches, cents indications may be added (downward deviations below and upward deviations above the respective accidental). The convention used is that the cents written refer to the tempered pitch implied by the flat, natural, or sharp sign and the note name. One of the great advantages of such a notation is that it allows the natural harmonic series to be precisely notated. A complete legend and fonts for the notation (see samples) are open source and available from Plainsound Music Edition.
s, where they describe distinctions between musical intervals that are eliminated by that tuning system. A comma can be viewed as the distance between two musical intervals. When a given comma is tempered out in a tuning system, the ability to distinguish between those two intervals in that tuning is eliminated. For example, the difference between the diatonic semitone and chromatic semitone is called the diesis. The widely used 12-tone equal temperament
tempers out the diesis, and thus does not distinguish between the two different types of semitones. On the other hand, 19-tone equal temperament does not temper out this comma, and thus it distinguishes between the two semitones.
Examples:
through a unique sequence of commas at increasing prime
limits
. The first comma of the comma sequence will be in the q-limit, where q is the nth odd prime, and n is the number of generators
. Subsequent commas will be in prime limits each one prime beyond the last.
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, a comma is a minute interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
, the difference resulting from tuning
Musical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
one note two different ways. The word "comma" used without qualification refers to the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
system, and another F tuned using the D-based quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
system. Even within the same tuning system, when scales with more than 12 notes are built, two notes which should coincide may have a different tuning. For example, in extended scales produced with 5-limit tuning an A tuned as a major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
below C5 and a G tuned as two major thirds above C4 will not be exactly the same note, as they would be in equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
. The difference between those notes, the diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
, also known as lesser diesis, is more than 40% of a semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
, and is easily audible.
Commas are often defined as the difference in size between two semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s, even within a single non-extended 12-tone scale
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
. Each meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
tuning system produces a 12-tone scale characterized by two different kinds of semitones (diatonic and chromatic), and hence by a comma of unique size. The same is true for Pythagorean tuning.
| |
In just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
, more than two kinds of semitones may be produced. Thus, a single tuning system may be characterized by several different commas. For instance, a commonly used version of 5-limit tuning produces a 12-tone scale with four kinds of semitones and four commas.
The size of commas is commonly expressed and compared in terms of cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
– 1/1200 fractions of an octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
on a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic scale.
Commas in different contexts
In the column labeled "Difference between semitoneSemitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s", m2 is the minor second (diatonic semitone), A1 is the augmented unison (chromatic semitone), and S1, S2, S3, S4 are semitones as defined here. In the columns labeled "Interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
1" and "Interval 2", all intervals are presumed to be tuned in just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
. Notice that the Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
(PC) and the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
(SC) are basic intervals which can be used as yardsticks to define some of the other commas. For instance, the difference between them is a small comma called schisma
Schisma
In music, the schisma is the ratio between a Pythagorean comma and a syntonic comma and equals 32805:32768, which is 1.9537 cents...
. A schisma is not audible in many contexts, as its size is narrower than the smallest noticeable difference
Just noticeable difference
In psychophysics, a just noticeable difference, customarily abbreviated with lowercase letters as jnd, is the smallest detectable difference between a starting and secondary level of a particular sensory stimulus...
between tones (which is around six cents).
| Name of comma | Alternative Name | Definitions | Size | ||||
|---|---|---|---|---|---|---|---|
| Difference between semitone Semitone A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.... s |
Difference between commas |
Difference between | Cents Cent (music) The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each... |
Ratio Interval ratio In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498... |
|||
| Interval Interval (music) In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads... 1 | Interval 2 | ||||||
| Schisma Schisma In music, the schisma is the ratio between a Pythagorean comma and a syntonic comma and equals 32805:32768, which is 1.9537 cents... |
Skhisma | A1 − m2 in 1/12-comma meantone Meantone temperament Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of... |
1 PC − 1 SC | 8 perfect fifths + 1 major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
5 octaves | 1.95 | 32805:32768 |
| Septimal kleisma Septimal kleisma In music, the ratio 225/224 is called the septimal kleisma .It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 2 . That says that it is the amount that two major thirds of 5/4 and a septimal... |
2 minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... s |
Septimal major third Septimal major third In music, the septimal major third , also called the supermajor third and sometimes Bohlen–Pierce third is the musical interval exactly or approximately equal to a just 9:7 ratio of frequencies, or alternately 14:11. It is equal to 435 cents, sharper than a just major third by the septimal... |
7.71 | 225:224 | |||
| Kleisma Kleisma In music theory and tuning, the kleisma, or semicomma majeur, is a minute and barely perceptible comma type interval important to musical temperaments. It is the difference between six justly tuned minor thirds and one justly tuned tritave or perfect twelfth... |
6 minor thirds | Tritave (1 octave Octave In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"... + 1 perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... ) |
8.11 | 15625:15552 | |||
| Small undecimal comma | 17.58 | 99:98 | |||||
| Diaschisma Diaschisma The diaschisma is a small musical interval defined as the difference between three octaves and four perfect fifths plus two major thirds . It can be represented by the ratio 2048:2025 and is about 19.5 cents... |
Diaskhisma | m2 − A1 in 1/6-comma meantone, S3 − S2 in 5-limit tuning |
2 SC − 1 PC | 3 octaves | 4 perfect fifths + 2 major thirds |
19.55 | 2048:2025 |
| Syntonic comma Syntonic comma In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents... (SC) |
Didymus' comma | S2 − S1 in 5-limit tuning |
4 perfect fifths | 2 octaves + 1 major third |
21.51 | 81:80 | |
| Major tone Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions... |
Minor tone | ||||||
| Pythagorean comma Pythagorean comma In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C... (PC) |
Ditonic comma | A1 − m2 in Pythagorean tuning Pythagorean tuning Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant... |
12 perfect fifths | 7 octaves | 23.46 | 531441:524288 | |
| Septimal comma | Minor seventh Minor seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the... |
Septimal minor seventh | 27.26 | 64:63 | |||
| Diesis Diesis In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents... |
Lesser diesis | m2 − A1 in 1/4-comma meantone Quarter-comma meantone Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning... , S3 − S1 in 5-limit tuning |
3 SC − 1 PC | Octave | 3 major thirds | 41.06 | 128:125 |
| Undecimal comma | Undecimal quarter-tone | Undecimal tritone | Perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
53.27 | 33:32 | ||
| Greater diesis | m2 − A1 in 1/3-comma meantone, S4 − S1 in 5-limit tuning |
4 SC − 1 PC | 4 minor thirds | Octave | 62.57 | 648:625 | |
| Tridecimal comma | Tridecimal third-tone | Tridecimal tritone | Perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
65.3 | 27:26 | ||
The syntonic comma has a crucial role in the history of music. It is the amount by which some of the notes produced in Pythagorean tuning were flattened or sharpened to produce just minor and major thirds. In Pythagorean tuning, the only highly consonant intervals were the perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
and its inversion, the perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
. The Pythagorean major third (81:64) and minor third (32:27) were dissonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
, and this prevented musicians from freely using triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
s and chord
Chord (music)
A chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
s, forcing them to write music with relatively simple texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
. In late Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
ratio of
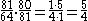
and at the same time E-G is sharpened to the just ratio of
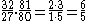
This brought to the creation of a new tuning system, known as quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
, which permitted the full development of music with complex texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
, such as polyphonic music
Polyphony
In music, polyphony is a texture consisting of two or more independent melodic voices, as opposed to music with just one voice or music with one dominant melodic voice accompanied by chords ....
, or melodies with instrumental accompaniment
Homophony
In music, homophony is a texture in which two or more parts move together in harmony, the relationship between them creating chords. This is distinct from polyphony, in which parts move with rhythmic independence, and monophony, in which all parts move in parallel rhythm and pitch. A homophonic...
. Since then, other tuning systems were developed, and the syntonic comma was used as a reference value to temper the perfect fifths in an entire family of them. Namely, in the family belonging to the syntonic temperament
Syntonic temperament
The syntonic temperament is a system of musical tuning in which the frequency ratio of each musical interval is a product of powers of an octave and a tempered perfect fifth, with the width of the tempered major third being equal to four tempered perfect fifths minus two octaves and the width of...
continuum, including meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
s.
Alternative definitions
In quarter-comma meantoneQuarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
, and any kind of meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
tuning system which tempers the fifth to a size smaller than 700 cents, the comma can be equivalently defined as:
- A diminished secondDiminished secondIn modern Western tonal music theory a diminished second is the interval between notes on two adjacent staff positions, or having adjacent note letters, whose alterations cause them, in ordinary equal temperament, to have no pitch difference, such as B and C or B and C...
, that is the difference between minor second (diatonic semitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
) and augmented unison (chromatic semitone). - The difference between major secondMajor secondIn Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
and diminished thirdDiminished thirdIn classical music from Western culture, a diminished third is the musical interval produced by narrowing a minor third by a chromatic semitone. For instance, the interval from A to C is a minor third, three semitones wide, and both the intervals from A to C, and from A to C are diminished thirds,...
. - The difference between minor thirdMinor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
and augmented secondAugmented secondIn classical music from Western culture, an augmented second is an interval produced by widening a major second by a chromatic semitone. For instance, the interval from C to D is a major second, two semitones wide, and both the intervals from C to D, and from C to D are augmented seconds, spanning...
. - The difference between major thirdMajor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
and diminished fourthDiminished fourthIn classical music from Western culture, a diminished fourth is an interval produced by narrowing a perfect fourth by a chromatic semitone. For example, the interval from C to F is a perfect fourth, five semitones wide, and both the intervals from C to F, and from C to F are diminished fourths,...
. - The difference between perfect fourthPerfect fourthIn classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
and augmented thirdAugmented thirdIn classical music from Western culture, an augmented third is an interval produced by widening a major third by a chromatic semitone. For instance, the interval from C to E is a major third, four semitones wide, and both the intervals from C to E, and from C to E are augmented thirds, spanning...
. - The difference between augmented fourth and diminished fifth.
- The difference between perfect fifthPerfect fifthIn classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
and diminished sixthDiminished sixthIn classical music from Western culture, a diminished sixth is an interval produced by narrowing a minor sixth by a chromatic semitone. For example, the interval from A to F is a minor sixth, eight semitones wide, and both the intervals from A to F, and from A to F are diminished sixths, spanning...
. - The difference between minor sixthMinor sixth-Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7....
and augmented fifthAugmented fifthIn classical music from Western culture, an augmented fifth is an interval produced by widening a perfect fifth by a chromatic semitone. For instance, the interval from C to G is a perfect fifth, seven semitones wide, and both the intervals from C to G, and from C to G are augmented fifths,...
. - The difference between major sixthMajor sixthIn classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two...
and diminished seventhDiminished seventhIn classical music from Western culture, a diminished seventh is an interval produced by narrowing a minor seventh by a chromatic semitone. For instance, the interval from A to G is a minor seventh, ten semitones wide, and both the intervals from A to G, and from A to G are diminished sevenths,...
. - The difference between minor seventhMinor seventhIn classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the...
and augmented sixthAugmented sixthIn classical music from Western culture, an augmented sixth is an interval produced by widening a major sixth by a chromatic semitone. For instance, the interval from C to A is a major sixth, nine semitones wide, and both the intervals from C to A, and from C to A are augmented sixths, spanning...
. - The difference between major seventhMajor seventhIn classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two...
and diminished octaveDiminished octaveIn classical music from Western culture, a diminished octave is an interval produced by narrowing a perfect octave by a chromatic semitone. As such, the two notes are denoted by the same letter but have different accidentals...
.
In Pythagorean tuning, and any kind of meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
tuning system which tempers the fifth to a size larger than 700 cents (such as 1/12-comma meantone), the comma is the opposite of the above mentioned differences. For instance, the Pythagorean comma is the opposite of a Pythagorean diminished second, i.e. it is the difference between chromatic semitone and diatonic semitone, rather than vice versa.
In each of the above mentioned tuning systems, these differences have all the same size. For instance, in Pythagorean tuning they are all equal to the opposite of a Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
, and in quarter-comma meantone they are all equal to a diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
.
Notation
In the years 2000-2004, Marc SabatMarc Sabat
Marc Sabat is a Canadian composer based in Berlin since 1999.-Works:He has made installations, video works and concert music pieces using acoustic instruments and, in some recent pieces, computer-generated electronics, drawing inspiration from investigations of the sounding and perception of small...
and Wolfgang von Schweinitz
Wolfgang von Schweinitz
Wolfgang von Schweinitz is a German composer of classical music.Schweinitz studied composition at the Hochschule für Musik und Theater Hamburg, from 1971 to 1973 with Gernot Klussmann and from 1973 to 1975 with György Ligeti. He continued his studies at the Stanford University with John Chowning...
worked together in Berlin to develop a method to exactly indicate pitches in staff notation. This method was called the extended Helmholtz-Ellis JI
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
pitch notation. Sabat and Schweinitz take the "conventional" flats, naturals and sharps as a Pythagorean series of perfect fifths. Thus, a series of perfect fifths beginning with F proceeds C G D A E B F# and so on. The advantage for musicians is that conventional reading of the basic fourths and fifths remains familiar. Such an approach has also been advocated by Daniel James Wolf
Daniel James Wolf
Daniel James Wolf is an American composer.- Studies :Wolf studied composition with Gordon Mumma, Alvin Lucier, and La Monte Young, as well as musical tunings with Erv Wilson and Douglas Leedy and ethnomusicology . Important contacts with Lou Harrison, John Cage, Walter Zimmermann...
and by Joe Monzo, who refers to it by the acronym HEWM (Helmholtz-Ellis-Wolf-Monzo). In the Sabat-Schweinitz design, syntonic commas are marked by arrows attached to the flat, natural or sharp sign, septimal commas using Giuseppe Tartini's symbol, and undecimal quartertones using the common practice quartertone signs (a single cross and backwards flat). For higher primes, additional signs have been designed. To facilitate quick estimation of pitches, cents indications may be added (downward deviations below and upward deviations above the respective accidental). The convention used is that the cents written refer to the tempered pitch implied by the flat, natural, or sharp sign and the note name. One of the great advantages of such a notation is that it allows the natural harmonic series to be precisely notated. A complete legend and fonts for the notation (see samples) are open source and available from Plainsound Music Edition.
Tempering of commas
Commas are frequently used in the description of musical temperamentMusical temperament
In musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
s, where they describe distinctions between musical intervals that are eliminated by that tuning system. A comma can be viewed as the distance between two musical intervals. When a given comma is tempered out in a tuning system, the ability to distinguish between those two intervals in that tuning is eliminated. For example, the difference between the diatonic semitone and chromatic semitone is called the diesis. The widely used 12-tone equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
tempers out the diesis, and thus does not distinguish between the two different types of semitones. On the other hand, 19-tone equal temperament does not temper out this comma, and thus it distinguishes between the two semitones.
Examples:
- 12-TET tempers out the diesis, as well as a variety of other commas.
- 19-TET tempers out the septimal diesisSeptimal diesisIn music, septimal diesis is an interval with the ratio of 49:48 , which is the difference between the septimal whole tone and the septimal minor third. It is about 35.7 cents wide, which is narrower than a quarter-tone but wider than the septimal comma...
and syntonic commaSyntonic commaIn music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, but does not temper out the diesis. - 22-TET tempers out the septimal commaSeptimal commaA septimal comma is a small musical interval in just intonation that contains the number seven in its prime factorization. There is more than one such interval, so the term septimal comma is ambiguous, but it most commonly refers to the interval 64/63....
of ArchytasArchytasArchytas was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato....
, but does not temper out the septimal diesis or syntonic comma. - 31-TET tempers out the syntonic comma, as well as the comma defined by the ratio (99:98), but does not temper out the diesis, septimal diesis, or septimal comma of Archytas.
Comma sequence
A comma sequence defines a musical temperamentMusical temperament
In musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
through a unique sequence of commas at increasing prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
limits
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
. The first comma of the comma sequence will be in the q-limit, where q is the nth odd prime, and n is the number of generators
Regular temperament
Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios...
. Subsequent commas will be in prime limits each one prime beyond the last.

